1.7. 特殊线性空间¶

1.7.1. 内积空间¶

什么是内积空间¶

内积空间 ( Inner product space ) : 在线性代数中, 内积空间是具有称为内积的附加结构的向量空间. 这个附加结构将空间中的每对向量与称为向量内积的标量量相关联. 内积允许严格引入直观的几何概念, 如向量的长度或两个向量之间的角度. 它们还提供了定义向量之间的正交性 (零内积) 的方法. 内积空间将欧氏空间 (其中内积是点积, 也称为标量积) 推广到任意 (可能是无限) 维的向量空间, 并在泛函分析中加以研究. 带内积的向量空间概念的首次使用是由于Peano在1898年提出的.

Definition 1.20 (内积空间)

设 \({\mathbb V}\) 是数域 \(\mathbb K\) 上的线性空间 (线性空间) , 对于 \({\mathbb V}\) 中的任意两个元素, 按某一规则定义一个实数 , 记为 \(\left\langle {{\bm{x}},{\bm{y}}} \right\rangle\) , 若它满足

交换律: \(\left\langle {{\bm{x}},{\bm{y}}} \right\rangle = \overline {\left\langle {{\bm{x}},{\bm{y}}} \right\rangle }\)
分配率: \(\left\langle {{\bm{x}},{\bm{y}} \oplus {\bm{z}}} \right\rangle = \left\langle {{\bm{x}},{\bm{y}}} \right\rangle + \left\langle {{\bm{x}},{\bm{z}}} \right\rangle\)
齐次性: \(\left\langle {k \odot {\bm{x}},{\bm{y}}} \right\rangle = k\left\langle {{\bm{x}},{\bm{y}}} \right\rangle\) , ( \(\forall k \in {\mathbb K}\) )
非负性: \(\left\langle {{\bm{x}},{\bm{x}}} \right\rangle \ge 0\) , 当且仅当 \({\bm x} = {\bm 0}\) , \(\left\langle {{\bm{x}},{\bm{x}}} \right\rangle = 0\)

则称 \(\left\langle {\bm x}, {\bm y} \right\rangle\) 为 \({\bm x}\) 与 \({\bm y}\) 的内积, 称 \({\mathbb V}\) 为 内积空间 (Inner product space).

警告

为什么不定义一个复数?

欧式空间(实内积空间)¶

当上述内积空间中的数域 \(\mathbb K\) 为实数域 \(\mathbb R\) 时, 称 \({\mathbb V}\) 为 欧式空间 (Euclid space) 或 实内积空间 .

酉空间(复内积空间)¶

当上述内积空间中的数域 \(\mathbb K\) 为实数域 \(\mathbb C\) 时, 称 \({\mathbb V}\) 为 酉空间 (Euclid space) 或 复内积空间 .

常见内积及其性质¶

定义¶

在复 \(n\) 维向量空间 \({\mathbb C}^n\) 中, 对于任意两个元素

\[{\bm x} = (\xi_1, \xi_2, \cdots, \xi_n) , {\bm y} = (\eta_1, \eta_2, \cdots, \eta_n) \]

定义它们的内积为

\[\left\langle {\bm x}, {\bm y} \right\rangle = \xi_1 \bar{\eta_1} + \xi_2 \bar{\eta_2} + \cdots + \xi_n \bar{\eta_n} = {\bm x}{\bm y}^H \]

上述定义对实 \(n\) 维向量空间 \({\mathbb R}^n\) 也成立.

性质¶

\(\left\langle {\bm x}, {\bm x} \right\rangle = \sum_{i=1}^n{|\xi_i|^2}\)
\(\left\langle {\bm x}, k{\bm y} \right\rangle = \bar{k} \left\langle {\bm x}, k{\bm y} \right\rangle\)
\(\left\langle {\bm x}, {\bm 0} \right\rangle = \left\langle {\bm 0}, {\bm x} \right\rangle = 0\)
\(\left\langle \sum_{i=1}^n\xi_i{\bm x}_i, \sum_{j=1}^n\eta_j{\bm y}_j \right\rangle = \sum_{i,j=1}^n \xi_i \bar{\eta_j}{\left\langle {\bm x}_i, {\bm y}_j \right\rangle}\)
长度: \(|{\bm x}| = \sqrt{\left\langle {\bm x}, {\bm x} \right\rangle}\)
夹角: \({\rm cos} ({\bm x}, {\bm y}) = \frac{\left\langle {\bm x}, {\bm y} \right\rangle}{|{\bm x}| |{\bm y}|}\) , 当 \(\left\langle {\bm x}, {\bm y} \right\rangle = 0\) 时, 称 \({\bm x}, {\bm y}\) 正交或垂直
Cauchy-不等式: \(\left\langle {\bm x}, {\bm y} \right\rangle \left\langle {\bm y}, {\bm x} \right\rangle \leq \left\langle {\bm x}, {\bm x} \right\rangle \left\langle {\bm y}, {\bm y} \right\rangle\)
任意线性无关的向量组可以用 Schmidt 正交化
任一非零酉空间都存在正交基和标准正交基
任一 \(n\) 维酉空间 \({\mathbb V}^n\) 均为其子空间 \({\mathbb V}_1\) 与 \({\mathbb V}_1^{\perp}\) 的和

度量矩阵¶

Schmidt正交化¶

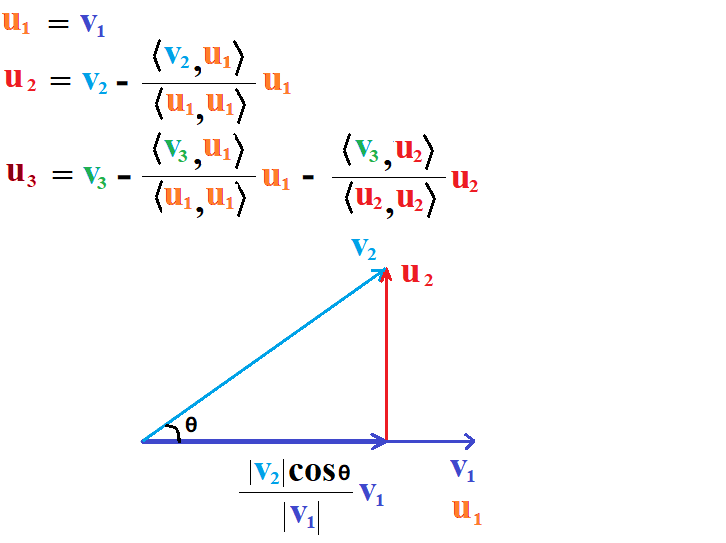
任给线性空间 \(\mathbb V\) 中的一组向量, 可以采用 Schmidt正交化 (Gram–Schmidt process) 方法正交化之, 其原理如图 1.7 所示, 动态示意图如图 1.7 所示.

图 1.6 Schmidt正交化图解¶

Schmidt正交化图解 (二维空间域三维空间)

图 1.7 Schmidt正交化动图示意¶

Schmidt正交化动图示意 (来自维基百科)

一般地, 设有内积空间 \({\mathbb V}^n\) 中的 \(m\) 个元素 \({\bm v}_1, {\bm v}_2, \cdots, {\bm v}_m\) \(1 \leq m \leq n, m\in {\mathbb Z}^+\) , 可以使用如下 Schmidt正交化步骤正交化它们:

\[\begin{array}{l} {{\bm{u}}_1} = {{\bm{v}}_1}\\ {{\bm{u}}_2} = {{\bm{v}}_2} - \frac{{\left\langle {{{\bm{v}}_2},{{\bm{u}}_1}} \right\rangle }}{{\left\langle {{{\bm{u}}_1},{{\bm{u}}_1}} \right\rangle }}{{\bm{u}}_1}\\ {{\bm{u}}_3} = {{\bm{v}}_3} - \frac{{\left\langle {{{\bm{v}}_3},{{\bm{u}}_1}} \right\rangle }}{{\left\langle {{{\bm{u}}_1},{{\bm{u}}_1}} \right\rangle }}{{\bm{u}}_1} - \frac{{\left\langle {{{\bm{v}}_3},{{\bm{u}}_2}} \right\rangle }}{{\left\langle {{{\bm{u}}_2},{{\bm{u}}_2}} \right\rangle }}{{\bm{u}}_2}\\ \vdots \\ {{\bm{u}}_m} = {{\bm{v}}_m} - \frac{{\left\langle {{{\bm{v}}_m},{{\bm{u}}_1}} \right\rangle }}{{\left\langle {{{\bm{u}}_1},{{\bm{u}}_1}} \right\rangle }}{{\bm{u}}_1} - \frac{{\left\langle {{{\bm{v}}_m},{{\bm{u}}_2}} \right\rangle }}{{\left\langle {{{\bm{u}}_2},{{\bm{u}}_2}} \right\rangle }}{{\bm{u}}_2} \cdots - \frac{{\left\langle {{{\bm{v}}_m},{{\bm{u}}_{m - 1}}} \right\rangle }}{{\left\langle {{{\bm{u}}_{m - 1}},{{\bm{u}}_{m - 1}}} \right\rangle }}{{\bm{u}}_{m - 1}} \end{array} \]

内积空间中线性变换¶

设 \({\bm e}_1, {\bm e}_2\) 为二维欧氏空间 \({\mathbb R}^2\) 的一组基, \({\mathbb R}^2\) 中的两个元素 \({\bm x}, {\bm y}\) 在该基下的坐标表示为 \({\bm x} = (\xi_1, \xi_2), {\bm y} = (\eta_1, \eta_2)\) , 线性变换 \(T\) 在该基下的矩阵为 \({\bm A} = \left[ {\begin{array}{ccc}a&b\\c&d\end{array}} \right]\) , 则有

\[\begin{array}{lll} {T{\bm{x}} = \left[ {\begin{array}{ccc} a&b\\ c&d \end{array}} \right]\left[ {\begin{array}{ccc} {{\xi _1}}\\ {{\xi _2}} \end{array}} \right] = \left[ {\begin{array}{ccc} {a{\xi _1} + b{\xi _2}}\\ {c{\xi _1} + d{\xi _2}} \end{array}} \right]}\\ {T{\bm{y}} = \left[ {\begin{array}{ccc} a&b\\ c&d \end{array}} \right]\left[ {\begin{array}{ccc} {{\eta _1}}\\ {{\eta _2}} \end{array}} \right] = \left[ {\begin{array}{ccc} {a{\eta _1} + b{\eta _2}}\\ {c{\eta _1} + d{\eta _2}} \end{array}} \right]} \end{array} \]

从而有

\[\left\langle {{\bm{x}},{\bm{y}}} \right\rangle = \left\langle {{{({\xi _1},{\xi _2})}^T},\;{{({\eta _1},{\eta _2})}^T}} \right\rangle = {\xi _1}{\eta _1} + {\xi _2}{\eta _2} \]

\[\begin{array}{lll} {\left\langle {T{\bm{x}},{\bm{y}}} \right\rangle = \left\langle {{{\left( {a{\xi _1} + b{\xi _2},\;c{\xi _1} + d{\xi _2}} \right)}^T},\;{{\left( {{\eta _1},{\eta _2}} \right)}^T}} \right\rangle }\\ {\;\;\;\;\;\;\;\;\;\; = (a{\xi _1} + b{\xi _2}){\eta _1} + (c{\xi _1} + d{\xi _2}){\eta _2}}\\ {\;\;\;\;\;\;\;\;\;\; = a{\xi _1}{\eta _1} + b{\xi _2}{\eta _1} + c{\xi _1}{\eta _2} + d{\xi _2}{\eta _2}} \end{array} \]

\[\begin{array}{lll} {\left\langle {{\bm{x}},T{\bm{y}}} \right\rangle = \left\langle {{{\left( {{\xi _1},{\xi _2}} \right)}^T},\;{{\left( {a{\eta _1} + b{\eta _2},\;c{\eta _1} + d{\eta _2}} \right)}^T}} \right\rangle }\\ {\;\;\;\;\;\;\;\;\;\; = {\xi _1}(a{\eta _1} + b{\eta _2}) + {\xi _2}(c{\eta _1} + d{\eta _2})}\\ {\;\;\;\;\;\;\;\;\;\; = a{\xi _1}{\eta _1} + b{\xi _1}{\eta _2} + c{\xi _2}{\eta _1} + d{\xi _2}{\eta _2}} \end{array} \]

\[\begin{array}{lll} {\left\langle {T{\bm{x}},T{\bm{y}}} \right\rangle = \left\langle {{{\left( {a{\xi _1} + b{\xi _2},\;c{\xi _1} + d{\xi _2}} \right)}^T},\;{{\left( {a{\eta _1} + b{\eta _2},\;c{\eta _1} + d{\eta _2}} \right)}^T}} \right\rangle }\\ {\;\;\;\;\;\;\;\;\;\;\;\; = (a{\xi _1} + b{\xi _2})(a{\eta _1} + b{\eta _2}) + (c{\xi _1} + d{\xi _2})(c{\eta _1} + d{\eta _2})}\\ {\;\;\;\;\;\;\;\;\;\;\;\; = {a^2}{\xi _1}{\eta _1} + {b^2}{\xi _2}{\eta _2} + ab{\xi _1}{\eta _2} + ab{\xi _2}{\eta _1} + }\\ {\;\;\;\;\;\;\;\;\;\;\;\;\;\;{c^2}{\xi _1}{\eta _1} + {d^2}{\xi _2}{\eta _2} + cd{\xi _1}{\eta _2} + cd{\xi _2}{\eta _1}}\\ {\;\;\;\;\;\;\;\;\;\;\;\;{\rm{ = }}({a^2} + {c^2}){\xi _1}{\eta _1} + ({b^2} + {d^2}){\xi _2}{\eta _2} + (ab + cd){\xi _1}{\eta _2} + (ab + cd){\xi _2}{\eta _1}} \end{array} \]

由 \(\left\langle {T{\bm{x}},{\bm{y}}} \right\rangle = \left\langle {{\bm{x}},T{\bm{y}}} \right\rangle\) 可以推出

\[b = c \]

由 \(\left\langle {T{\bm{x}},{\bm{y}}} \right\rangle = -\left\langle {{\bm{x}},T{\bm{y}}} \right\rangle\) 可以推出

\[b = -c \]

由 \(\left\langle{\bm x}, {\bm y}\right\rangle = \left\langle T{\bm x}, T{\bm y}\right\rangle\) 可以推出

\[\left\{ {\begin{array}{ccc}{{a^2} + {c^2} = 1}\\{{b^2} + {d^2} = 1}\\{ab + cd = 0}\end{array}} \right. \]

实对称变换¶

设 \(T\) 是欧氏空间 \({\mathbb V}\) 的一个线性变换, 且对 \({\mathbb V}\) 中的任意两个元素 \({\bm x}, {\bm y}\) 有

\[\left\langle T{\bm x}, {\bm y}\right\rangle = \left\langle {\bm x}, T{\bm y}\right\rangle , \]

则称 \(T\) 是 \({\mathbb V}\) 中的 实对称变换 , 一般简称为 对称变换 .

对称变换在标准正交基下的矩阵满足

\[{\bm A}^T = {\bm A} \]

称为 实对称矩阵 ( Symmetric matrix ) , 其中, \({\bm A}^T\) 为 \({\bm A}\) 的 转置矩阵 (也可以是共轭转置, 实数的共轭为其自身), 即有 \(a_{ij} = a_{ji}\) .

注解

欧式空间的线性变换 \(T\) 是实对称变换 \(\leftrightarrow\) \(T\) 在标准正交基下的矩阵为实对称矩阵;
实对称矩阵的特征值都是实数;
实对称矩阵的不同特征值对应特征向量正交.

实反对称变换¶

设 \(T\) 是欧氏空间 \({\mathbb V}\) 的一个线性变换, 且对 \({\mathbb V}\) 中的任意两个元素 \({\bm x}, {\bm y}\) 有

\[\left\langle T{\bm x}, {\bm y}\right\rangle = -\left\langle {\bm x}, T{\bm y}\right\rangle , \]

则称 \(T\) 是 \({\mathbb V}\) 中的 实反对称变换 , 一般简称为 反对称变换 .

反对称变换在标准正交基下的矩阵满足

\[{\bm A}^T = -{\bm A} \]

称为 实反对称矩阵 ( Skew-symmetric matrix ) , 其中, \({\bm A}^T\) 为 \({\bm A}\) 的 转置矩阵 (也可以是共轭转置, 实数的共轭为其自身), 即有 \(a_{ij} = -a_{ji}\) .

正交变换¶

设 \({\mathbb V}\) 是欧氏空间, \(T\) 是 \({\mathbb V}\) 的一个线性变换, 若 \(T\) 对 \({\mathbb V}\) 中的任意元素 \({\bm x}， {\bm y}\) 满足

\[\left\langle{\bm x}, {\bm y}\right\rangle = \left\langle T{\bm x}, T{\bm y}\right\rangle , \]

那么称 \(T\) 是线性空间 \({\mathbb V}\) 的一个 正交变换 ( Orthogonal transformation ).

正交变换在标准正交基下的矩阵满足

\[{\bm Q}^T{\bm Q} = {\bm Q}{\bm Q}^T = {\bm I} 或 {\bm Q}^{-1} = {\bm Q}^T \]

称为 正交矩阵 .

提示

正交变换是保持图形形状和大小不变的几何变换, 包含旋转, 平移, 轴对称及上述变换的复合.
正交变换可以保证向量的长度和两个向量之间的夹角不变.
正交变换将正交基映射到正交基.
二维或三维欧氏空间中的正交变换是刚性旋转、反射或旋转和反射的组合.

容易验证, 旋转变换是正交变换

逆时针旋转: \(\left[ {\begin{array}{lll}{\cos \theta }&{ - \sin \theta }\\{\sin \theta }&{\cos \theta }\end{array}} \right]\left[ {\begin{array}{ccc}{{x_1}}\\{{x_2}}\end{array}} \right] = \left[ {\begin{array}{ccc}{{x_1}\cos \theta - {x_2}\sin \theta }\\{{x_1}\sin \theta + {x_2}\cos \theta }\end{array}} \right]\)
顺时针旋转: \(\left[ {\begin{array}{lll}{\cos \theta }&{\sin \theta }\\{ - \sin \theta }&{\cos \theta }\end{array}} \right]\left[ {\begin{array}{ccc}{{x_1}}\\{{x_2}}\end{array}} \right] = \left[ {\begin{array}{ccc}{{x_1}\cos \theta + {x_2}\sin \theta }\\{ - {x_1}\sin \theta + {x_2}\cos \theta }\end{array}} \right]\)

注解

设 \({\bm x}, {\bm y}\) 是欧氏空间中的元素, 则有

\[\begin{array}{lll} {T{\bm{x}} = \left[ {\begin{array}{lll} {\cos \theta }&{ - \sin \theta }\\ {\sin \theta }&{\cos \theta } \end{array}} \right]\left[ {\begin{array}{ccc} {{x_1}}\\ {{x_2}} \end{array}} \right] = \left[ {\begin{array}{ccc} {{x_1}\cos \theta - {x_2}\sin \theta }\\ {{x_1}\sin \theta + {x_2}\cos \theta } \end{array}} \right]}\\ {T{\bm{y}} = \left[ {\begin{array}{lll} {\cos \theta }&{ - \sin \theta }\\ {\sin \theta }&{\cos \theta } \end{array}} \right]\left[ {\begin{array}{ccc} {{y_1}}\\ {{y_2}} \end{array}} \right] = \left[ {\begin{array}{ccc} {{y_1}\cos \theta - {y_2}\sin \theta }\\ {{y_1}\sin \theta + {y_2}\cos \theta } \end{array}} \right]} \end{array} \]

从而有

\[\begin{array}{lll} \begin{array}{l} \left\langle {T{\bm{x}},T{\bm{y}}} \right\rangle = ({\xi _1}\cos \theta - {\xi _2}\sin \theta )({\eta _1}\cos \theta - {\eta _2}\sin \theta )\\ \;\;\;\;\;\;\;\;\;\;\;\; + ({\xi _1}\sin \theta + {\xi _2}\cos \theta )({\eta _1}\sin \theta + {\eta _2}\cos \theta )\\ \;\;\;\;\;\;\;\;\;\;\;\; = {\xi _1}{\eta _1}{\cos ^2}\theta + {\xi _2}{\eta _2}{\sin ^2}\theta - {\xi _1}{\eta _2}\sin \theta \cos \theta - {\xi _2}{\eta _1}\sin \theta \cos \theta \end{array}\\ {\;\;\;\;\;\;\;\;\;\;\;\; + {\xi _1}{\eta _1}{{\sin }^2}\theta + {\xi _2}{\eta _2}{{\cos }^2}\theta + {\xi _1}{\eta _2}\sin \theta \cos \theta + {\xi _2}{\eta _1}\sin \theta \cos \theta }\\ {\;\;\;\;\;\;\;\;\;\;\;\; = {\xi _1}{\eta _1} + {\xi _2}{\eta _2} = \left\langle {{\bm{x}},{\bm{y}}} \right\rangle } \end{array} \]

酉对称变换¶

设 \(T\) 是欧氏空间 \({\mathbb V}\) 的一个线性变换, 且对 \({\mathbb V}\) 中的任意两个元素 \({\bm x}, {\bm y}\) 有

\[\left\langle T{\bm x}, {\bm y}\right\rangle = \left\langle {\bm x}, T{\bm y}\right\rangle , \]

则称 \(T\) 是 \({\mathbb V}\) 中的 酉对称变换 .

酉对称变换在标准正交基下的矩阵满足

\[{\bm A}^H = {\bm A} \]

称为 Hermite矩阵 ( Hermitian matrix ) 或 酉对称矩阵 , 其中, \({\bm A}^H\) 为 \({\bm A}\) 的 共轭转置转置 矩阵, 即有 \(a_{ij} = \bar{a_{ji}}\) .

注解

酉空间的线性变换 \(T\) 是酉对称变换 \(\leftrightarrow\) \(T\) 在标准正交基下的矩阵为酉对称矩阵, 即hermite矩阵;
酉对称矩阵的特征值都是实数;
酉对称矩阵的不同特征值对应特征向量正交.

反酉对称变换¶

设 \(T\) 是欧氏空间 \({\mathbb V}\) 的一个线性变换, 且对 \({\mathbb V}\) 中的任意两个元素 \({\bm x}, {\bm y}\) 有

\[\left\langle T{\bm x}, {\bm y}\right\rangle = -\left\langle {\bm x}, T{\bm y}\right\rangle , \]

则称 \(T\) 是 \({\mathbb V}\) 中的 反酉对称变换 .

反酉对称变换在标准正交基下的矩阵满足

\[{\bm A}^H = -{\bm A} \]

称为 反Hermite矩阵 ( Skew-Hermitian matrix ) 或 反酉对称矩阵 , 其中, \({\bm A}^H\) 为 \({\bm A}\) 的 共轭转置转置 矩阵, 即有 \(a_{ij} = -\bar{a_{ji}}\) .

酉变换¶

设 \({\mathbb V}\) 是酉空间, \(T\) 是 \({\mathbb V}\) 的一个线性变换, 若 \(T\) 对 \({\mathbb V}\) 中的任意元素 \({\bm x}， {\bm y}\) 满足

\[\left\langle{\bm x}, {\bm y}\right\rangle = \left\langle T{\bm x}, T{\bm y}\right\rangle , \]

那么称 \(T\) 是线性空间 \({\mathbb V}\) 的一个 酉变换 ( Unitary transformation ).

酉变换在标准正交基下的矩阵满足

\[{\bm A}^H{\bm A} = {\bm A}{\bm A}^H = {\bm I} \]

称为 酉矩阵 .

提示

复内积空间的酉变换对于实内积空间的正交变换.
酉变换可以保证向量的长度和两个向量之间的夹角不变.
酉变换将正交基映射到正交基.

设 \({\bm A} \in {\mathbb C}^{n \times n}\) , 且满足

\[{\bm A}^H{\bm A} = {\bm A}{\bm A}^H \]

则称 \({\bm A}\) 为 正规矩阵 .

Givens 旋转变换¶

Givens 变换 ( Givens transformation ) , 也称 Givens 旋转 (Givens rotation), 是描述将某一平面内的向量进行旋转的线性变换. 如下图所示为二维平面内的旋转变换:

一般地, 在 \(n\) 维欧式空间 \({\mathbb R}^n\) 中, 设 \({\bm e}_1, {\bm e}_2, \cdots, {\bm e}_n\) 是一组标准正交基, 在平面 \([{\bm e}_i, {\bm e}_j]\) 中可定义旋转变换

\[{\bm{G}}_{i,j,\theta} = \mathop {\left[ {\begin{array}{ccccccccccc} 1&{}&{}&{}&{}&{}&{}&{}&{}&{}&{}\\ {}& \ddots &{}&{}&{}&{}&{}&{}&{}&{}&{}\\ {}&{}&1&{}&{}&{}&{}&{}&{}&{}&{}\\ {}&{}&{}&c&{}&{}&{}&{ s}&{}&{}&{}\\ {}&{}&{}&{}&1&{}&{}&{}&{}&{}&{}\\ {}&{}&{}&{}&{}& \ddots &{}&{}&{}&{}&{}\\ {}&{}&{}&{}&{}&{}&1&{}&{}&{}&{}\\ {}&{}&{}&{-s}&{}&{}&{}&c&{}&{}&{}\\ {}&{}&{}&{}&{}&{}&{}&{}&1&{}&{}\\ {}&{}&{}&{}&{}&{}&{}&{}&{}& \ddots &{}\\ {}&{}&{}&{}&{}&{}&{}&{}&{}&{}&1 \end{array}} \right]}\limits_{\begin{array}{ccccccccccc} {}&i&{}&{}&{}&{}&{}&{}&{}&j&{} \end{array}} \]

其中, \(c^2 + s^2 = 1\) , \(c = {\rm cos}\theta, s = {\rm sin}\theta\) 称其为 Givens 矩阵 , 也称 初等旋转矩阵 , 所对应的线性变换称为 Givens 变换 , 也称 初等旋转变换 ,

性质:

正交: \({\bm G}_{i,j,\theta}^{-1} = {\bm G}_{i,j,\theta}^{T} = {\bm G}_{i,j, -\theta}\)
\({\rm det}({\bm G}_{i,j,\theta}) = 1\)

设 \({\bm x} = (\xi_1, \xi_2, \cdots, \xi_n)^T\) , \({\bm y} = {\bm{G}}_{i,j,\theta }{\bm x} = (\eta_1, \eta_2, \cdots, \eta_n)^T\) 则选取如下的 \(c, s\) , 可以使得 \(\eta_i = \sqrt{\xi_i^2 + \xi_j^2} > 0 , \eta_j = 0\)

\[c = {\rm cos}\theta = \frac{\xi_i}{\sqrt{\xi_i^2 + \xi_j^2}}, s = {\rm sin}\theta = \frac{\xi_j}{\sqrt{\xi_i^2 + \xi_j^2}} \]

定理: 设 \({\bm x} = (\xi_1, \xi_2, \cdots, \xi_n)^T \neq = {\bm 0}\) , 则存在有限个Givens矩阵的乘积 \({\bm G} = {\bm G}_{1,n,\theta_{n-1}}{\bm G}_{1,n-1,\theta_{n-2}} \cdots {\bm G}_{1,2,\theta_1}\) , 使得 \({\bm G}{\bm x} = |{\bm x}|{\bm e}_1\) , 其中

\({\bm G}_{1,2,\theta_{1}}\) 满足: \(c = {\rm cos}{\theta_{1}} = \frac{\xi_1}{\sqrt{\xi_1^2 + \xi_2^2}}, s = {\rm sin}\theta_1 = \frac{\xi_2}{\sqrt{\xi_1^2 + \xi_2^2}}\)
\({\bm G}_{1,3,\theta_{2}}\) 满足: \(c = {\rm cos}{\theta_{2}} = \frac{\sqrt{\xi_1^2 + \xi_2^2}}{\sqrt{\xi_1^2 + \xi_2^2 + \xi_3^2}}, s = {\rm sin}\theta_2 = \frac{\xi_3}{\sqrt{\xi_1^2 + \xi_2^2 + \xi_3^2}}\)
\(\vdots\)
\({\bm G}_{1,n-1,\theta_{n-2}}\) 满足: \(c = {\rm cos}{\theta_{n-2}} = \frac{\sqrt{\xi_1^2+\xi_2^2+\cdots+\xi_{n-2}^2}}{\sqrt{\xi_1^2+\xi_2^2+\cdots+\xi_{n-2}^2+\xi_{n-1}^2}}, s = {\rm sin}\theta_{n-2} = \frac{\xi_{n-1}}{\sqrt{\xi_1^2+\xi_2^2+\cdots+\xi_{n-2}^2+\xi_{n-1}^2}}\)
\({\bm G}_{1,n,\theta_{n-1}}\) 满足: \(c = {\rm cos}{\theta_{n-1}} = \frac{\sqrt{\xi_1^2+\xi_2^2+\cdots+\xi_{n-1}^2}}{\sqrt{\xi_1^2+\xi_2^2+\cdots+\xi_{n-1}^2+\xi_n^2}}, s = {\rm sin}\theta_{n-1} = \frac{\xi_n}{\sqrt{\xi_1^2+\xi_2^2+\cdots+\xi_{n-1}^2+\xi_n^2}}\)

注解

举个例子, 设 \({\bm x} = (2, 4, 4)^T\) , 用Givens变换, 将 \({\bm x}\) 化为与 \({\bm e}_1\) 同方向的向量.

解: 由题意, 构造

\({\bm G}_{1,2,\theta_{1}} = \left[ {\begin{array}{ccc}{\frac{{\rm{1}}}{{\sqrt {\rm{5}} }}}&{\frac{{{\rm{ 2}}}}{{\sqrt {\rm{5}} }}}&{\rm{0}}\\{\frac{{\rm{-2}}}{{\sqrt {\rm{5}} }}}&{\frac{{\rm{1}}}{{\sqrt {\rm{5}} }}}&{\rm{0}}\\{\rm{0}}&{\rm{0}}&{\rm{1}}\end{array}} \right]\) , 使得 \({\bm G}_{1,2,\theta_{1}}{\bm x} = (\frac{10}{\sqrt 5}, 0, 4)^T\) , 其中 \(c = {\rm cos}{\theta_{1}} = \frac{\xi_1}{\sqrt{\xi_1^2 + \xi_2^2}} = \frac{2}{\sqrt{2^2 + 4^2}} = \frac{1}{\sqrt 5}\), \(s = {\rm sin}\theta_1 = \frac{\xi_2}{\sqrt{\xi_1^2 + \xi_2^2}} = \frac{4}{\sqrt{2^2 + 4^2}} = \frac{2}{\sqrt 5}\)
\({\bm G}_{1,3,\theta_{2}} = \left[ {\begin{array}{ccc}{\frac{{\sqrt {\rm{5}} }}{{\rm{3}}}}&{\rm{0}}&{\frac{{\rm{2}}}{{\rm{3}}}}\\{\rm{0}}&{\rm{1}}&{\rm{0}}\\{\frac{{{\rm{ - 2}}}}{{\rm{3}}}}&{\rm{0}}&{\frac{{\sqrt {\rm{5}} }}{{\rm{3}}}}\end{array}} \right]\) 使得 \({\bm G}_{1,3,\theta_{2}}({\bm G}_{1,2,\theta_{1}}{\bm x}) = (6, 0, 0)^T\) , 其中 \(c = {\rm cos}{\theta_{2}} = \frac{\sqrt{2^2 + 4^2}}{\sqrt{2^2 + 4^2 + 4^2}} = \frac{\sqrt 5}{3}\), \(s = {\rm sin}\theta_2 = \frac{4 }{\sqrt{2^2 + 4^2 + 4^2}} = \frac{2}{3}\)

提示

由于旋转变换不改变向量的长度, 如上述例子, 变换前后长度均为 \(6\) , 所以在计算 \(c, s\) 时可以根据原始坐标 \({\bm x} = (\xi_1, \xi_2, \cdots, \xi_n)^T\) 计算.

警告

如果 Givens 矩阵定义为逆时针旋转的矩阵, 即将 \({\bm{G}}_{i,j,\theta}\) 中的 \(s\) 变为 \(-s\) , 那么上述相应的结论做对应的改变即可.

Householder 反射变换¶

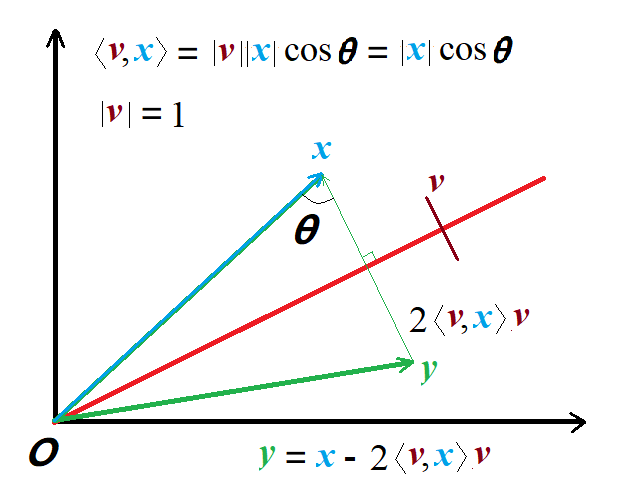
Householder 变换 ( Householder transformation ) 也称为Householder反射 (Householder reflection), 是描述包含原点的平面或超平面的反射的线性变换. 反射超平面可以通过与其正交的单位向量 \({\bm v}\) 来定义, 点 \({\bm x}\) 关于此超平面的映射是一个线性变换, 定义如下:

\[{\bm y} = {\bm x}-2\left\langle {\bm v}, {\bm x} \right\rangle {\bm v} = {\bm x} - 2{\bm v}({\bm v}^H{\bm x}) = ({\bm I} - 2{\bm v}{\bm v}^H){\bm x} = {\bm H}{\bm x} , \]

其中, \({\bm v}\) 是单位列向量. \({\bm H}\) 称为 Householder矩阵 , 也称 初等反射矩阵 , 所对应的线性变换称为 Householder变换 ( Householder transformation ), 如图 1.8 所示.

图 1.8 二维空间中的 Householder 变换.¶

二维空间中的 Householder 变换. 其中, \({\bm v}\) 为超平面的单位法向量.

性质:

对称: \({\bm H}^H = {\bm H}\)
自逆: \({\bm H}^{-1} = {\bm H}\)
对合: \({\bm H}^2 = {\bm I}\)
正交: \({\bm H}^H{\bm H} = {\bm I}\)
\({\rm det}({\bm H}) = -1\)

定理: 设 \({\bm x} = (\xi_1, \xi_2, \cdots, \xi_n)^T \neq {\bm 0}\) 单位列向量 \({\bm z}\) , 则存在Householder矩阵 \({\bm H}\) , 使得 \({\bm H}{\bm x} = |{\bm x}|{\bm z}\) , 其中

\[{\bm H} = {\bm I} - 2{\bm v}{\bm v}^H \]

且

\[{\bm v} = \frac{{\bm x} - |{\bm x}|{\bm z}}{|{\bm x} - |{\bm x}|{\bm z}|} \]

注解

举个例子, 设 \({\bm x} = (2, 4, 4)^T\) , 用 Householder 变换, 将 \({\bm x}\) 化为与 \({\bm e}_1\) 同方向的向量.

解: 由题意, 有

\({\bm x} - |{\bm x}|{\bm e}_1 = (2,4,4)^T-6(1,0,0)^T = (-4, 4, 4)^T\)

且 \({\bm v} = \frac{{\bm x} - |{\bm x}|{\bm e}_1}{|{\bm x} - |{\bm x}|{\bm e}_1|} = \frac{(-4, 4, 4)^T}{\sqrt{4^2+4^2+4^2}} = (\frac{-1}{\sqrt 3}, \frac{1}{\sqrt 3}, \frac{1}{\sqrt 3})^T\)

则 \({\bm H} = {\bm I} - 2{\bm v}{\bm v}^H = \left[ {\begin{array}{ccc}{\frac{{\rm{1}}}{{\rm{3}}}}&{\frac{{\rm{2}}}{{\rm{3}}}}&{\frac{{\rm{2}}}{{\rm{3}}}}\\{\frac{{\rm{2}}}{{\rm{3}}}}&{\frac{{\rm{1}}}{{\rm{3}}}}&{\frac{{{\rm{ - 2}}}}{{\rm{3}}}}\\{\frac{{\rm{2}}}{{\rm{3}}}}&{\frac{{{\rm{ - 2}}}}{{\rm{3}}}}&{\frac{{\rm{1}}}{{\rm{3}}}}\end{array}} \right]\) 使得 \({\bm H}{\bm x} = (6, 0, 0)^T\) .

谱分解¶

对于 \(n\) 阶Hermite矩阵 \({\bm A}\) , 存在 \(n\) 阶酉矩阵 \({\bm P}\) , 使得

\[{\bm P}^H{\bm A}{\bm P} = {\bm \Lambda } = {\rm diag}(\lambda_1, \lambda_2, \cdots, \lambda_n) \]

即有

\[{\bm A} = {\bm P}{\bm \Lambda }{\bm P}^H = \lambda_1({\bm p}_1 {\bm p}_1^H) + \lambda_2({\bm p}_2 {\bm p}_2^H) + \cdots + \lambda_n({\bm p}_n {\bm p}_n^H) \]

其中, \(\lambda_i (i=1,2,\cdots, n)\) 是 \({\bm A}\) 的特征值. 称上式为矩阵 \({\bm A}\) 的 谱分解 ( Spectral decomposition )

1.7.2. 总结¶

当复内积空间的内积定义为 \(\left\langle {{\bm{x}},{\bm{y}}} \right\rangle = {\bm{x}}{{\bm{y}}^H}\) (行向量) 或 \(\left\langle {{\bm{x}},{\bm{y}}} \right\rangle = {\bm{x}}^H{{\bm{y}}}\) (列向量) 时,

欧式空间 –> 实内积空间
酉空间 –> 复内积空间
实內积空间与复内积空间一一对应
实正交变换对应酉变换
实对称变换对应酉对称变换
正交变换在标准正交基下的矩阵为正交矩阵
对称变换在标准正交基下的矩阵为实对称矩阵
酉变换在标准正交基下的矩阵为酉矩阵
酉对称变换在标准正交基下的矩阵为酉对称矩阵