1.1. 线性空间¶
1.1.1. 基础概念¶
域¶
域: 一种集合
数域: 满足四则运算封闭
事件域: 满足交并补运算封闭
映射¶
像: 映射后, 相当于因变量
原像: 映射前, 相当于自变量
相等: 变换后相同, \(\sigma_1\), \(\sigma_2\) 是集合\(S_1\)到\(S_2\)的映射, 若 \(\forall a \in S_1\), 有\(\sigma_1(a) = \sigma_2(a)\), 则 \(\sigma_1 = \sigma_2\)
乘积: 设 \(\sigma\), \(\tau\) 分别为 \(S\) 到 \(S_1\), \(S_1\)到\(S_2\)的映射, 则映射的乘积定义为 \((\tau\sigma)(a) = \tau(\sigma(a))\)
1.1.2. 线性空间概念及性质¶
定义¶
涉及一个集合和一个数域, 五种运算, 分别为:
集合内
加法(元素的加法): \(\oplus\)
数域内
加法(数的加法): \(+\)
乘法(数的乘法): \(\times\) 或省略
集合与数域间
乘法(数乘): \(\odot\)
给定数域 \({\mathbb K}\), 非空集合 \({\mathbb V}\), 定义集合内的加法运算(\(\oplus\))和数域与集合间的数乘运算(\(\odot\)), 若满足以下条件, 则称 \({\mathbb V}\) 是数域 \({\mathbb K}\) 上的 线性空间 ( Linear Space ) .
运算封闭性:
加法封闭性: 对 \(\forall {\bm x}, {\bm y} \in {\mathbb V}\), 有唯一的和 \({\bm x} \oplus {\bm y} ∈ {\mathbb V}\)
数乘封闭性: 对 \(\forall k \in {\mathbb K}, \forall {\bm x} \in {\mathbb V}\), 有唯一的元素 \(\forall k {\bm x} \in {\mathbb V}\)
交换律: \({\bm x} \oplus {\bm y} = {\bm y} \oplus {\bm x}\)
结合律: \(({\bm x} \oplus {\bm y}) \oplus {\bm z} = {\bm x} \oplus ({\bm y} \oplus {\bm z})\)
有零元: \(\forall {\bm x} \in {\mathbb V}, \exists {\bm 0} \in {\mathbb V}\) 使得 \({\bm x} \oplus {\bm 0} = {\bm x}\)
有负元: \(\forall {\bm x} \in {\mathbb V}, \exists {\bm y} \in {\mathbb V}\) 使得 \({\bm x} \oplus {\bm y} = {\bm 0}\)
乘1律: \(1 \odot {\bm x} = {\bm x}\)
数因子分配律: \(k \odot (\bm{x} + \bm{y}) = k \odot {\bm x} + k \odot {\bm y}\)
数乘分配律: \((k+l) \odot {\bm x} = k \odot {\bm x} + l \odot {\bm x}\)
数乘结合律: \(k \odot (l \odot {\bm x}) = (kl) \odot {\bm x}\)
性质¶
\(\forall {\bm x} \in {\mathbb V}, 0,1\in {\mathbb K}\), 有:
\(0 \odot {\bm x} = {\bm 0}\): 数 \(0\) 乘以 \({\mathbb V}\) 中任意元素 \({\bm x}\) 的结果为 \({\mathbb V}\) 中零元素 \({\bm 0}\)
\(1 \odot {\bm x} = {\bm x}\): 数 \(1\) 乘以 \({\mathbb V}\) 中任意元素 \({\bm x}\) 的结果仍为元素 \({\bm x}\)
\(-1 \odot {\bm x} = - {\bm x}\): 数 \(-1\) 乘以 \({\mathbb V}\) 中任意元素 \({\bm x}\) 的结果为\({\bm x}\)的负元素 \(-{\bm x}\)
注解
\((0 \odot {\bm x}) \oplus {\bm x} = (0 + 1) \odot {\bm x} = {\bm x}\) \(\Longrightarrow\) \(0 \odot {\bm x} = {\bm 0}\)
\((-1 \odot {\bm x}) \oplus {\bm x} = (-1 + 1) \odot {\bm x} = {\bm x} = 0 \odot {\bm x} = {\bm 0}\) \(\Longrightarrow\) \(-1 \odot {\bm x}\) 为 \({\bm x}\) 的负元素
\(k \odot ({\bm x} \oplus (-1\odot{\bm x})) = k\odot {\bm x} \oplus k \odot (- {\bm x}) = k \odot {\bm x} \oplus (-1)\odot(k\odot {\bm x}) = {\bm 0}\)
线性组合与线性表示¶
设 \({\bm x}_1, {\bm x}_2, \cdots, {\bm x}_m\) 为线性空间 \({\mathbb V}\) 中的 \(m\) 个元素, \({\bm x} \in {\mathbb V}\) , 若存在数 \(c_1, c_2, \cdots, c_m \in {\mathbb K}\) , 使
则称 \({\bm x}\) 为 \({\bm x}_1, {\bm x}_2, \cdots, {\bm x}_m\) 的 线性组合 (Linear Combination), 也称 \({\bm x}\) 可由 \({\bm x}_1, {\bm x}_2, \cdots, {\bm x}_m\) 线性表示 (Linear Representation).
注解
对比稀疏表示, 字典学习:
原子可看作上述向量;
字典可看作上述向量组;
稀疏表示系数就是上述线性组合系数.
线性相关与线性无关¶
设 \({\bm x}_1, {\bm x}_2, \cdots, {\bm x}_m\) 为线性空间 \({\mathbb V}\) 中的 \(m\) 个元素, 若 存在一组不全为零的数 \(c_1, c_2, \cdots, c_m \in {\mathbb K}\) , 使
则称 \({\bm x}_1, {\bm x}_2, \cdots, {\bm x}_m\) 线性相关 ( Linearly Dependent ), 否则, 称其 线性无关 ( Linearly Independent ).
提示
若 \({\bm x}_1, {\bm x}_2, \cdots, {\bm x}_m\) 线性无关, 则当且仅当 \(c_1, c_2, \cdots, c_m \in {\mathbb K}\) 全为零时, \(c_1 \odot {\bm x}_1 \oplus c_2 \odot {\bm x}_2 \oplus \cdots \oplus c_m \odot {\bm x}_m = {\bm 0}\) 成立.
1.1.3. 线性空间的基、坐标与维数¶
定义¶
设 \({\mathbb V}\) 是数域 \({\mathbb K}\) 上的线性空间, \({\bm x}_1, {\bm x}_2, \cdots, {\bm x}_n (n \geq 1)\) 是属于 \({\mathbb V}\) 的任意 \(n\) 个元素, 若它们满足:
\({\bm x}_1, {\bm x}_2, \cdots, {\bm x}_n (n \geq 1)\) 线性无关;
\(\forall {\bm x} \in {\mathbb V}\) , 均可由 \({\bm x}_1, {\bm x}_2, \cdots, {\bm x}_n (n \geq 1)\) 线性表示, 记为
\[{\bm x} = {\xi}_1 \odot {\bm x}_1 \oplus {\xi}_2 \odot {\bm x}_2 \oplus \cdots \oplus {\xi}_n \odot {\bm x}_n \]
则称
\({\bm x}_1, {\bm x}_2, \cdots, {\bm x}_n (n \geq 1)\) 是 \({\mathbb V}\) 一个 基 或 基底 ;
\({\xi}_1, {\xi}_2, \cdots, {\xi}_n (n \geq 1)\) 为 \({\bm x}\) 在该基下的 坐标.
\({\mathbb V}\) 中最大线性无关的元素的数目为线性空间 \(\mathbb V\) 的 维数, 记为 \({\rm dim}({\mathbb V})\)
提示
基不一定是向量, 可能是矩阵, 或者其它更为抽象的;
坐标是数.
1.1.4. 基变换与坐标变换¶
从一个基到另一个基时, 坐标的变化.
提示
以下部分, 在不引起混淆时, 对集合内的加法 ( \(\oplus\) ) 与数域内的加法 ( \(+\) ) , 及数乘 ( \(\odot\) ) 与数域内的乘法 (\(\times\) 或省略 ) 不作区分.
两个基之间的转换¶
基变换: 设 \({\bm x}_1, {\bm x}_2, \cdots, {\bm x}_n\) 是 \({\mathbb V}^{n}\) 的旧基, \({\bm y}_1, {\bm y}_2, \cdots, {\bm y}_n\) 是 \({\mathbb V}^{n}\) 的新基, 则有
写成矩阵形式为
即:
同理可得从新基变回旧基的表达式:
显然, :\({\bm{A}} = {\bm{C}}^{-1}\)
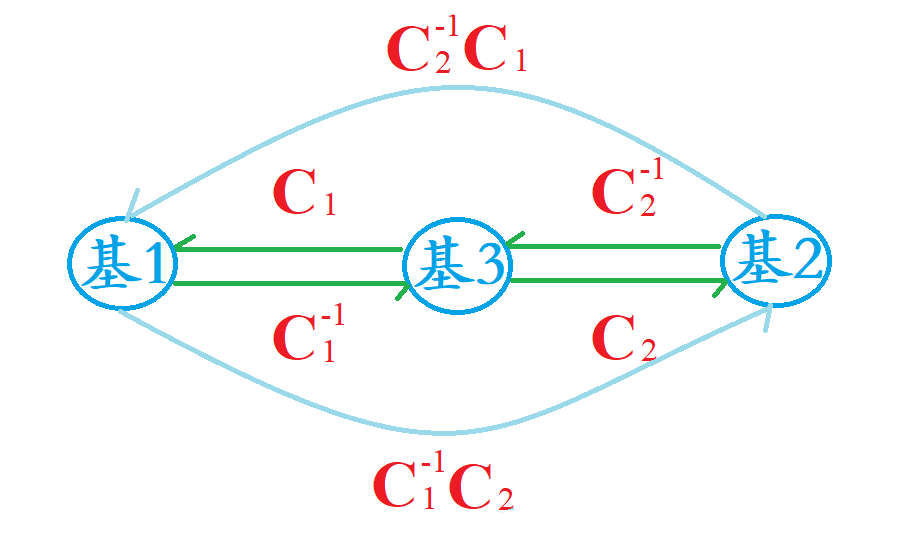
多个基之间的转换¶
设有线性空间 :\({\mathbb V}^n\) , 及其三个基:
基1: \({\bm X}_1, {\bm X}_2, \cdots, {\bm X}_n\)
基2: \({\bm Y}_1, {\bm Y}_2, \cdots, {\bm Y}_n\)
基3: \({\bm Z}_1, {\bm Z}_2, \cdots, {\bm Z}_n\)
且设由基3到基1的过度矩阵为 \({\bm C}_1\) , 且由基3到基2的过度矩阵为 \({\bm C}_2\) , 则由基1到基2的过度矩阵为 \({\bm C}_1^{-1}{\bm C}_2\) 由基2到基1的过度矩阵为 \({\bm C}_2^{-1}{\bm C}_1\) , 即
坐标变换¶
坐标变换: 设向量 \(\bm z\) 在上述旧基与新基下可表示为:
则
从而有
由此得坐标变换公式