1.4. 特征值与特征向量

如何选择线性空间的基, 使得线性变换在该基下的矩阵表示最为简单. 涉及 特征值(eigenvalue) 与特征向量(eigenvector)

1.4.1. 特征值与特征向量

线性变换的特征值与特征向量

Definition 1.11 (线性变换的特征值与特征向量)

设 $T$ 是数域 ${\mathbb K}$ 上的线性空间 ${\mathbb V}^n$ 上的线性变换, 且对于数域 ${\mathbb K}$ 中的数 $\lambda$ , 若存在非零向量 ${\bm x} \in {\mathbb V}^n$ 满足如下条件

$T{\bm x} = \lambda {\bm x}$

则称 $\lambda$ 为 $T$ 的 特征值 , ${\bm x}$ 为 $T$ 的属于特征值 $\lambda$ 的特征向量.

注解

由上述定义知:

• 线性变换不改变特征向量的方向

• 特征值被特征向量唯一确定, 特征向量不被特征值唯一确定( $T(k{\bm x}) = k\lambda {\bm x}$ )

矩阵的特征值与特征向量

Definition 1.12 (矩阵的特征值与特征向量)

设有矩阵 ${\bm A}$ , 且对于数域 ${\mathbb K}$ 中的数 $\lambda$ , 若存在非零向量 ${\bm x} \in {\mathbb V}^n$ 满足如下条件

${\bm A}{\bm x} = \lambda {\bm x}$

则称 $\lambda$ 为矩阵 ${\bm A}$ 的 特征值 , ${\bm x}$ 为 ${\bm A}$ 的属于特征值 $\lambda$ 的特征向量.

特征值与特征向量的关系

注解

• 特征值被特征向量唯一确定, 特征向量不被特征值唯一确定( $T(k{\bm x}) = k\lambda {\bm x}$ )

• 互不相同的特征值对应的特征向量线性无关

实例

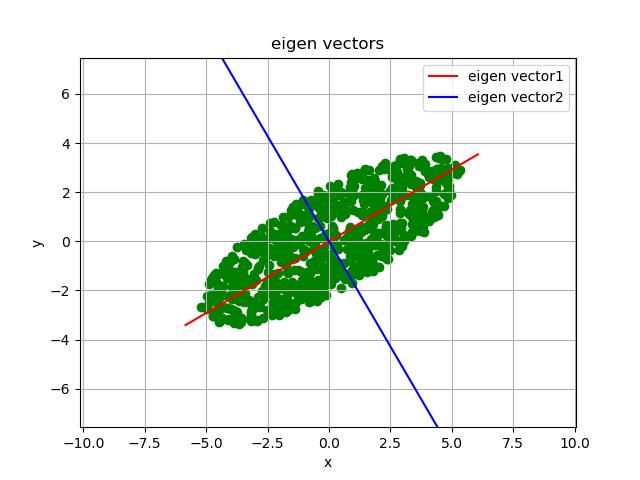
编程生成二维平面 $(x, y)$ 中的点, 这些点落在一个椭圆内, 长轴为 $6$ , 短轴为 $2$ , 如 图 1.5 所示, 其主要的方向有两个, 长轴方向(红色), 短轴方向(蓝).

对这些二维数据做主成分分析 ( Principal Component Analysis, PCA), 可得两个主要方向:

1. 零均值化数据

2. 计算数据的协方差(即两个维度间的)

3. 计算协方差矩阵的特征值与特征向量

图 1.5 椭圆内点的特征向量可视化

对椭圆内的点进行特征分解, 得到两个特征方向, 并进行特征向量可视化, 长轴(红), 短轴(蓝).

警告

注意这里是对数据的协方差矩阵作特征值分解, 是否可以不求协方差矩阵直接对原始数据矩阵进行分析得到主方向. 特征值特征向量是针对变换矩阵而言的, 对数据矩阵是否有相关理论.

实现代码, 参见文件 demo_eigen_ellipse.py .

代码 1.2 demo_eigen_ellipse.py

import pytool
import numpy as np
import matplotlib.pyplot as plt

# =====================generate Ellipse=====================
a = 6  # major axis
b = 2  # minor axis
x0 = 10  # center x0
y0 = 10  # center y0
N = 1000  # number of points

# angle for rotating ellipse data
theta = np.pi * 30 / 180

x, y = pytool.ellipse_surface(a, b, x0, y0, N, 'rand')
# x, y = pytool.ellipse_surface(a, b, x0, y0, N, 'order')


x = x - np.mean(x)
y = y - np.mean(y)

xse = [min(x), max(x)]
yse = [min(y), max(y)]


xy = np.array([x, y])
print(xy.shape)

A = xy

# ========================rotate============================
# ------------rotating matrix(Anti-clockwise)---------------
M = [[np.cos(theta), np.sin(theta)],
     [-np.sin(theta), np.cos(theta)]]
M = [[np.cos(theta), -np.sin(theta)],
     [np.sin(theta), np.cos(theta)]]
print("rotating matrix M: ", M)

# -----------------------rotating---------------------------
A = np.dot(M, A)

x = A[0]
y = A[1]

# ========================show data=========================
plt.figure()
plt.scatter(x, y, c='g', marker='o')
plt.grid()

# ==================Eigenvalue decomposition================

AAT = np.dot(A, A.transpose())
ATA = np.dot(A.transpose(), A)

evalues, evectors = np.linalg.eig(AAT)
# evalues, evectors = np.linalg.eig(ATA)
print(A.shape, AAT.shape, evalues.shape, evectors.shape)
print(AAT)
print("evalues: ", evalues, "evectors: ", evectors)
angle1 = np.arctan(evectors[1, 0] / evectors[0, 0]) * 180 / np.pi
angle2 = np.arctan(evectors[1, 1] / evectors[0, 1]) * 180 / np.pi
print(angle1, angle2)


# =====================plot eigen vector=====================
colorlines = ['-r', '-b']
pytool.plot_vectors2d(evectors.transpose(), xse=xse, yse=yse,
                      nPoints=N, title='eigen vectors', colorlines=colorlines)
plt.legend(['eigen vector1', 'eigen vector2'])
plt.show()


plt.figure()
plt.imshow(AAT)
plt.show()

1.4.2. 广义特征向量

概念与内涵

一般, 若 $\lambda^*$ 是矩阵 ${\bm A}$ 的 $k$ 重特征值, 则对应的线性无关的特征向量 ${\bm x}_1, {\bm x}_2, \cdots, {\bm x}_k$ 可由下列方程组求出

$(\lambda^* {\bm I}-{\bm A}){\bm x}_i = - {\bm x}_{i-1}$

其中, $i = 1, 2, \cdots, k$ , 且规定 ${\bm x}_0 = {\bm 0}$ , 将求得的 $k$ 个向量 ${\bm x}_1, {\bm x}_2, \cdots, {\bm x}_k$ 称为矩阵 ${\bm A}$ 的 广义特征向量 .

计算步骤

1. 写出特征多项式矩阵 $\lambda {\bm I}-{\bm A}$

2. 令特征多项式矩阵对应的行列式的值为 $|\lambda {\bm I}-{\bm A}| = 0$

3. 求解得特征值 $\lambda$

4. 对于单重特征值: 代入方程组 $(\lambda {\bm I}-{\bm A}){\bm x} = {\bm 0}$ , 求解特征向量.

5. 对于多重特征值: 代入方程组 $(\lambda^* {\bm I}-{\bm A}){\bm x}_i = - {\bm x}_{i-1}$ , 求解广义特征向量.

1.4.3. 例子(广义特征向量)

注解

求如下矩阵的特征值与特征向量/广义特征向量

${\bm{A}} = \left[ {\begin{array}{ccc} 0&2&2\\ 2&1&2\\ 0&2&1 \end{array}} \right]$

解:

1. 特征多项式矩阵为

$\lambda {\bm I}-{\bm A} = {\left[ {\begin{array}{ccc} \lambda &{ - 2}&{ - 2}\\ { - 2}&{\lambda - 1}&{ - 2}\\ 0&{ - 2}&{\lambda - 1} \end{array}} \right]}$

可使用初等变换稍微化简, 方便求行列式的值 $|\lambda {\bm I}-{\bm A}| = {{{(\lambda + 1)}^2}(\lambda - 4)}$

2. 求解 $|\lambda {\bm I}-{\bm A}| = {{{(\lambda + 1)}^2}(\lambda - 4)} = 0$ 的解为 $\lambda_1 = 4, \lambda_2 = \lambda_3 = -1$

3. 由 $(\lambda_1 {\bm I}-{\bm A}){\bm x}_1 = {\bm 0}$ 求解出对应于 $\lambda_1$ 的特征向量 ${\bm x}_1 = (5, 6, 4)^T$ , 由 $(\lambda_2 {\bm I}-{\bm A}){\bm x}_2 = {\bm 0}$ , $(\lambda_3 {\bm I}-{\bm A}){\bm x}_3 = -{\bm x}_2$ 求解广义特征向量 ${\bm x}_2 = (0, 1, -1)^T$ , ${\bm x}_3 = (1, -1, 1/2)^T$

1.4.4. 特征多项式与最小多项式

特征多项式

设 $T$ 是 ${\mathbb V}^n$ 中的线性变换, ${\bm x}_1, {\bm x}_2, \cdots, {\bm x}_n$ 是线性空间 ${\mathbb V}^n$ 中的基, $T$ 在该基下的矩阵为 ${\bm A}$ , 再设 ${\bm x} = {\xi}_1 {\bm x}_1 + {\xi}_2 {\bm x}_2 + \cdots + {\xi}_n {\bm x}_n$ 为 $T$ 的属于特征值 $\lambda$ 的特征向量, 则由 $T{\bm x} = \lambda {\bm x}$ 知

${\bm A}\left[ {\begin{array}{lll}{{\xi _1}}\\{{\xi _2}}\\ \vdots \\{{\xi _n}}\end{array}} \right] = \lambda \left[ {\begin{array}{lll}{{\xi _1}}\\{{\xi _2}}\\ \vdots \\{{\xi _n}}\end{array}} \right]$

从而有

$(\lambda {\bm I} - {\bm A}) \left[ {\begin{array}{lll}{{\xi _1}}\\{{\xi _2}}\\ \vdots \\{{\xi _n}}\end{array}} \right] = {\bm 0}$

由 ${\bm x} \neq {\bm 0}$ 知, ${\xi _1}, {\xi _2}, \cdots, {\xi _n}$ 不全为零, 从而方程组有非零解, 则

${\varphi}(\lambda) = {\rm det}(\lambda {\bm I} - {\bm A}) = \left | \lambda {\bm I} - {\bm A} \right | = (\lambda - \lambda_1)(\lambda - \lambda_2)\cdots(\lambda - \lambda_n)$

Definition 1.13 (特征多项式)

设有数域 ${\mathbb K}$ 上的 $n$ 阶方阵 ${\bm A}$ , 变量 $\lambda$ , 矩阵 ${\bm A}$ 的 特征矩阵 $\lambda {\bm I} - {\bm A}$ 的行列式 ${\rm det}(\lambda {\bm I} - {\bm A})$ 称为矩阵 ${\bm A}$ 的 特征多项式 . 记为 $\varphi (\lambda)$ , 其根 $\lambda_i$ 为 ${\bm A}$ 的 特征值 , 非零解向量 :$({\xi _1}, {\xi _2}, \cdots, {\xi _n})^T$ 为 ${\bm A}$ 的属于特征值 $\lambda_i$ 的 特征向量 .

注解

线性变换 $T$ 的特征值与特征向量, 与 $T$ 的矩阵 ${\bm A}$ 的特征值与特征向量一一对应:

• $T$ 与 ${\bm A}$ 的特征值一致

• $T$ 的特征向量在基下的坐标与 ${\bm A}$ 的特征向量一致

• 线性变换 $T$ 的矩阵 ${\bm A}$ 的特征多项式与基的选择无关

即, 若 ${\bm A}$ 为 $T$ 在基 ${\bm x}_1, {\bm x}_2, \cdots, {\bm x}_n$ 下的矩阵, $({\xi _1}, {\xi _2}, \cdots, {\xi _n})^T$ 为矩阵 ${\bm A}$ 的属于特征值 $\lambda$ 的特征向量, 则

• $\lambda$ 是 $T$ 的特征值

• ${\bm x} = {\xi}_1 {\bm x}_1 + {\xi}_2 {\bm x}_2 + \cdots + {\xi}_n {\bm x}_n$ 是 $T$ 的属于特征值 $\lambda$ 的特征向量

• 线性变换 $T$ 的矩阵 ${\bm A}$ 的特征多项式与基的选择无关

Theorem 1.14 (Hamilton-Cayley)

$n$ 阶矩阵 ${\bm A}$ 是其特征多项式 ${\varphi}(\lambda)$ 的矩阵根. 即若有

${\varphi}(\lambda) = {\rm det}(\lambda {\bm I} - {\bm A}) = \lambda^n + a_1\lambda^{n-1} + \cdots + a_{n-1}\lambda + a_n$

则

${\varphi}({\bm A}) = {\bm A}^n + a_1{\bm A}^{n-1} + \cdots + a_{n-1}{\bm A} + a_n{\bm I} = {\bm O}.$

最小多项式

Definition 1.15 (最小多项式)

定义: 首项系数是1, 次数最小, 且以矩阵 ${\bm A}$ 为根的 $\lambda$ 的多项式, 称为 ${\bm A}$ 的 最小多项式 (MinimalPolynomial) , 常用 $m(\lambda)$ 表示.

1.4.5. 特征子空间与不变子空间

什么是特征子空间

Definition 1.16 (特征子空间)

定义: 设 $T$ 是线性空间 ${\mathbb V}^n$ 的线性变换, $\lambda$ 是 $T$ 的一个特征值, 称 ${\mathbb V}^n$ 的子空间 ${\mathbb V}^n_{\lambda}$ 是 $T$ 的属于 $\lambda$ 的 特征子空间 (Characteristic Subspace) , 其中

${\mathbb V}^n_{\lambda} = \{ {\bm x} | T{\bm x} = \lambda {\bm x} , {\bm x} \in {\mathbb V}^n \}.$

提示

1. 特征子空间是线性子空间

2. 特征子空间是由特征向量加上零向量构成的子空间.

什么是不变子空间

Definition 1.17 (不变子空间)

若 $T$ 是线性空间 ${\mathbb V}$ 的线性变换, ${\mathbb V}_1$ 是 ${\mathbb V}$ 的子空间, 且 $\forall {\bm x} \in {\mathbb V}_1$ , 有 $T{\bm x} \in {\mathbb V}_1$ , 则称 ${\mathbb V}_1$ 是 $T$ 的 不变子空间 (Invariant Subspace).

1.4.6. 信号子空间与噪声子空间

在数字信号处理领域经常定义 信号子空间 (Signal Subspace) 与 噪声子空间 (Noise Subspace)