1.3. 线性变换及其表示¶

1.3.1. 线性变换¶

什么是线性变换¶

Definition 1.8 (变换)

设\({\mathbb V}\)是数域\(\mathbb K\)上的线性空间, \(T\)是\({\mathbb V}\)到自身的一个映射, 使得对于 \(\forall {\bm x} \in {\mathbb V}\), \({\mathbb V}\)中都有唯一的向量\(\bm y\)与之对应, 则称 \(T\) 是\({\mathbb V}\)的一个变换或算子 , 记为

\[T {\bm x} = {\bm y} \]

称\({\bm y}\)为\({\bm x}\)在\(T\)下的象, \({\bm x}\) 为 \({\bm y}\) 的原象.

警告

\(T\)是\({\mathbb V}\)到自身的一个映射: 即变换前后都在线性空间\({\mathbb V}\)中, 如果变换前后不在同一线性空间中?.
定义中说明了\({\mathbb V}\)中的元素为向量, 实际上\({\mathbb V}\)中元素不一定是向量.

Definition 1.9 (线性变换)

设\(T\)是数域\(K\)上线性空间\({\mathbb V}\)中的一个变换, 对于\(\forall k, l\in K\), 若满足

\[T(k{\bm x} \oplus l{\bm y}) = kT({\bm x}) \oplus lT(\bm y) \]

则称\(T\)是\({\mathbb V}\)的线性变换.

线性变换的特性¶

若线性空间 \({\mathbb V}\) 中的 \({\bm x}_1, {\bm x}_2, \cdots, {\bm x}_m\) 线性相关, 则线性变换 \(T\) 对其变换后仍线性相关.

即若存在不全为零的数 \(c_1, c_2, \cdots, c_m \in K\) , 使得

\[c_1 \odot {\bm x}_1 \oplus c_2 \odot {\bm x}_2 \oplus \cdots \oplus c_m \odot {\bm x}_m = {\bm 0} \]

成立, 则亦有下式成立

\[c_1 \odot (T{\bm x}_1) \oplus c_2 \odot (T{\bm x}_2) \oplus \cdots \oplus c_m \odot (T{\bm x}_m) = T{\bm 0} = {\bm 0} \]

1.3.2. 线性变换的运算¶

涉线性变换的加法, 数乘, 乘法, 逆与幂, 以及单位变换, 零变换, 负变换, 逆变换, 多项式. 有关对称变换, 正交变换, 酉变换参见特殊线性空间小节

提示

可以证明上述变换均为线性变换!

基本线性变换¶

单位变换¶

将线性空间 \({\mathbb V}\) 中的任一元素 \({\bm x}\) 变为自身的变换称为 单位变换 , 即

\[(T_e){\bm x} = {\bm x} , \ (\forall {\bm x} \in {\mathbb V}) \]

零变换¶

将线性空间 \({\mathbb V}\) 中的任一元素 \({\bm x}\) 变为零元素 \({\bm 0}\) 的变换称为 零变换 , 即

\[(T_0){\bm x} = {\bm 0} , \ (\forall {\bm x} \in {\mathbb V}) \]

负变换¶

设 \(T\) 是线性空间 \({\mathbb V}\) 的线性变换, 线性变换 \(T\) 的 负变换 定义为

\[(-T){\bm x} = -(T{\bm x}) , \ (\forall {\bm x} \in {\mathbb V}) \]

逆变换¶

设 \(T, T^{-1}\) 是线性空间 \({\mathbb V}\) 的线性变换, 若满足下述条件, 则称线性变换 \(T\) 与 \(T^{-1}\) 互为 逆变换 (Inverse transformation) , 即

\[(T T^{-1}){\bm x} = (T^{-1} T){\bm x} = {\bm x} , \ (\forall {\bm x} \in {\mathbb V}) \]

亦即:

\[(T T^{-1}) = (T^{-1} T) = T_e \]

加法¶

定义¶

设 \(T_1, T_2\) 是线性空间 \({\mathbb V}\) 的两个线性变换, 线性变换的加法定义为

\[(T_1 + T_2){\bm x} = T_1{\bm x} \oplus T_2{\bm x}, \ (\forall {\bm x} \in {\mathbb V}) \]

性质¶

交换律: \(T_1 + T_2 = T_2 + T_1\)
结合律: \((T_1 + T_2) + T_3 = T_1 + (T_2 + T_3)\)
有零元: \(T + T_0 = T\)
有负元: \(T + (-T) = T_0\)

提示

对照线性空间定义中的加法的性质.

数乘¶

定义¶

设 \(k \in K\) , \(T\) 为线性空间 \({\mathbb V}\) 的线性变换, 定义数 \(k\) 与变换 \(T\) 的乘积( 数乘 ) \(kT\) 为

\[(kT){\bm x} = k\odot(T{\bm x}) , \ (\forall {\bm x} \in {\mathbb V}) \]

性质¶

乘1律: \(1T = T\)
数因子分配律: \(k(T_1 + T_2) = kT_1 + kT_2\)
数乘分配率: \((k + l)T = kT + lT\)
数乘结合率: \((kl)T = k(lT)\)

提示

对照线性空间定义中的数乘的性质.

乘法¶

定义¶

设 \(T_1, T_2\) 是线性空间 \({\mathbb V}\) 的两个线性变换, 定义 \(T_1\) 与 \(T_2\) 的乘积 \(T_1T_2\) 为

\[(T_1T_2){\bm x} = T_1(T_2 {\bm x}) , \ (\forall {\bm x} \in {\mathbb V}) \]

性质¶

结合律: \((T_1T_2)T_3 = T_1(T_2T_3)\)
分配律1: \(T_1(T_2 + T_3) = T_1T_2 + T_1T_3\)
分配率2: \((T_1 + T_2)T_3 = T_1T_3 + T_2T_3\)

幂¶

定义¶

设 \(n\) 是正整数, \(T\) 是线性空间 \({\mathbb V}\) 中的线性变换, 定义其 \(n\) 次幂为

\[T^n = T^{n-1}T , \ (n=2,3,\cdots) \]

定义 \(T\) 的 零次幂 为:

\[T^0 = T_e \]

性质¶

性质1: \(T^{m+n} = T^m T^n\)
性质2: \((T^m)^n = T^{mn}\)
性质3: \(T^{(-n)} = (T^{-1})^n\)

线性变换的多项式¶

定义¶

数量 \(t\) 的 \(m\) 次多项式可以定义为

\[f(t) = a_m t^m + a_{m-1} t^{m-1} + \cdots + a_1t + a_0 \]

类似地, 线性变换 \(T\) 的 \(m\) 次多项式可以定义为

\[f(T) = a_m T^m + a_{m-1} T^{m-1} + \cdots + a_1T + a_0 \]

性质¶

性质1: 若 \(h(t) = f(t)g(t)\) , 则 \(h(T) = f(T)g(T)\)
性质2: 若 \(p(t) = f(t) + g(t)\) , 则 \(p(T) = f(T) + g(T)\)
性质3: \(f(T)g(T) = g(T)f(T)\) (同一线性变换的多项式相乘可交换)

1.3.3. 线性变换与矩阵¶

线性变换的矩阵表示¶

设 \(T\) 是线性空间 \({\mathbb V}\) 中的线性变换, \({\bm x} \in {\mathbb V}^n\) , 且 \({\bm x}_1 , {\bm x}_2 , \cdots, {\bm x}_n\) 是 \({\mathbb V}^n\) 的一个基 (原象基组), 则

\[{\bm x} = a_1\odot{\bm x}_1 \oplus a_2\odot{\bm x}_2 \oplus \cdots \oplus a_n\odot{\bm x}_n \]

\[T{\bm x} = a_1\odot(T{\bm x}_1) \oplus a_2\odot(T{\bm x}_2) \oplus \cdots \oplus a_n\odot(T{\bm x}_n) \]

故 \({\bm x}\) 在变换 \(T\) 下得到的象 \(T{\bm X}\) 可以由基象组线性表示, 而基像组仍在线性空间 \({\mathbb V}\) 中, 故可用原象组线性表示为

\[\left\{ {\begin{array}{ccc} {T{{\bm{x}}_1} = {a_{11}}\odot{{\bm{x}}_1} \oplus {a_{21}}\odot{{\bm{x}}_2} \oplus \cdots \oplus {a_{n1}}\odot{{\bm{x}}_n}}\\ {T{{\bm{x}}_2} = {a_{12}}\odot{{\bm{x}}_1} \oplus {a_{22}}\odot{{\bm{x}}_2} \oplus \cdots \oplus {a_{n2}}\odot{{\bm{x}}_n}}\\ \vdots \\ {T{{\bm{x}}_n} = {a_{1n}}\odot{{\bm{x}}_1} \oplus {a_{2n}}\odot{{\bm{x}}_2} \oplus \cdots \oplus {a_{nn}}\odot{{\bm{x}}_n}} \end{array}} \right. \]

将上述方程组矩阵化可得, 线性变换 \(T\) 在基 \({\bm x}_1 , {\bm x}_2 , \cdots, {\bm x}_n\) 下的矩阵表示为

\[T({\bm x}_1 , {\bm x}_2 , \cdots, {\bm x}_n) = (T{\bm x}_1 , T{\bm x}_2 , \cdots, T{\bm x}_n) = ({\bm x}_1 , {\bm x}_2 , \cdots, {\bm x}_n){\bm A} \]

其中

\[{\bm A} = \left[ {\begin{array}{cccc}{{a_{11}}}&{{a_{12}}}& \cdots &{{a_{1n}}}\\{{a_{21}}}&{{a_{22}}}& \cdots &{{a_{2n}}}\\ \vdots & \vdots &{}& \vdots \\{{a_{n1}}}&{{a_{n2}}}& \cdots &{{a_{nn}}}\end{array}} \right] \]

矩阵 \({\bm A}\) 的第 \(i\) 列为 \(T{\bm x}_i\) 的坐标. 当 \(\oplus\) 表示普通向量加法, \(\odot\) 表示普通数与向量乘法时, 上式退化为普通矩阵乘.

注解

举个例子, 定义线性空间 \({\mathbb R}^{2\times 2}\) 中的线性变换

\[T{\bm X} = \left[ {\begin{array}{cc} a&b\\ c&d \end{array}} \right] {\bm X} \]

求线性变换 \(T\) 在基 \({\bm E}_{11}, {\bm E}_{12}, {\bm E}_{21}, {\bm E}_{22}\) 下的矩阵.

解: 由题意有

\[\left\{ {\begin{array}{ccc} {T{{\bm{E}}_{11}} = \left[ {\begin{array}{ccc} a&b\\ c&d \end{array}} \right]\left[ {\begin{array}{ccc} 1&0\\ 0&0 \end{array}} \right] = \left[ {\begin{array}{ccc} a&0\\ c&0 \end{array}} \right] = a{{\bm{E}}_{11}} + c{{\bm{E}}_{21}}}\\ {T{{\bm{E}}_{12}} = \left[ {\begin{array}{ccc} a&b\\ c&d \end{array}} \right]\left[ {\begin{array}{ccc} 0&1\\ 0&0 \end{array}} \right] = \left[ {\begin{array}{ccc} 0&a\\ 0&c \end{array}} \right] = a{{\bm{E}}_{12}} + c{{\bm{E}}_{22}}}\\ {T{{\bm{E}}_{21}} = \left[ {\begin{array}{ccc} a&b\\ c&d \end{array}} \right]\left[ {\begin{array}{ccc} 0&0\\ 1&0 \end{array}} \right] = \left[ {\begin{array}{ccc} b&0\\ d&0 \end{array}} \right] = b{{\bm{E}}_{11}} + d{{\bm{E}}_{21}}}\\ {T{{\bm{E}}_{22}} = \left[ {\begin{array}{ccc} a&b\\ c&d \end{array}} \right]\left[ {\begin{array}{ccc} 0&0\\ 0&1 \end{array}} \right] = \left[ {\begin{array}{ccc} 0&b\\ 0&d \end{array}} \right] = b{{\bm{E}}_{12}} + d{{\bm{E}}_{22}}} \end{array}} \right. \]

由上式得到 \(T\) 在所给基下的矩阵为

\[{\bm A} = \left[ {\begin{array}{cccc} a&0&b&0\\ 0&a&0&b\\ c&0&d&0\\ 0&c&0&d \end{array}} \right] \]

满足 \(T({\bm E}_{11}, {\bm E}_{12}, {\bm E}_{21}, {\bm E}_{22}) = ({\bm E}_{11}, {\bm E}_{12}, {\bm E}_{21}, {\bm E}_{22}) {\bm A}\)

提示

零变换的矩阵为零矩阵: \({\bm O}\)
单位变换的矩阵为单位矩阵: \({\bm I}\)
数乘变换的矩阵为数量矩阵: \(m{\bm I}\)

性质¶

\((T_1 + T_2)({\bm x}_1 , {\bm x}_2 , \cdots, {\bm x}_n) = ({\bm x}_1 , {\bm x}_2 , \cdots, {\bm x}_n)({\bm A}+{\bm B})\)
\((kT_1)({\bm x}_1 , {\bm x}_2 , \cdots, {\bm x}_n) = ({\bm x}_1 , {\bm x}_2 , \cdots, {\bm x}_n)(k{\bm A})\)
\((T_1 T_2)({\bm x}_1 , {\bm x}_2 , \cdots, {\bm x}_n) = ({\bm x}_1 , {\bm x}_2 , \cdots, {\bm x}_n){\bm A}{\bm B}\)
\((T_1^{-1})({\bm x}_1 , {\bm x}_2 , \cdots, {\bm x}_n) = ({\bm x}_1 , {\bm x}_2 , \cdots, {\bm x}_n){\bm A}^{-1}\)

像与原像的坐标转换¶

设有线性空间 \({\mathbb V}^n\) 中的元素 \({\bm x}\) , 线性变换 \(T\) , 一组基 \({\bm x}_1 , {\bm x}_2 , \cdots, {\bm x}_n\) ; \({\bm x}\) 在该基下的坐标为 \((\xi_1, \xi_2, \cdots, \xi_n)^T\) , \(T\) 在该基下的的矩阵为 \({\bm A}\) ; 则 \(T{\bm x}\) 在该基下的坐标为

\[\left[ {\begin{array}{lll}{{\eta _1}}\\{{\eta _2}}\\ \vdots \\{{\eta _n}}\end{array}} \right] = {\bm{A}}\left[ {\begin{array}{lll}{{\xi _1}}\\{{\xi _2}}\\ \vdots \\{{\xi _n}}\end{array}} \right] \]

提示

\[T{\bm{x}} = T({{\bm{x}}_1},\;{{\bm{x}}_2}, \cdots ,{{\bm{x}}_n})\left[ {\begin{array}{lll}{{\xi _1}}\\{{\xi _2}}\\ \vdots \\{{\xi _n}}\end{array}} \right] = ({{\bm{x}}_1},\;{{\bm{x}}_2}, \cdots ,{{\bm{x}}_n}){\bm{A}}\left[ {\begin{array}{lll}{{\xi _1}}\\{{\xi _2}}\\ \vdots \\{{\xi _n}}\end{array}} \right] \]

线性变换在不同基下的矩阵转换¶

设有线性空间 \({\mathbb V}^n\) 中的线性变换 \(T\) , 在基 \({\bm x}_1 , {\bm x}_2 , \cdots, {\bm x}_n\) 和基 \({\bm y}_1 , {\bm y}_2 , \cdots, {\bm y}_n\) 下的矩阵分别为 \({\bm A}, {\bm B}\) , 且由基1到基2的过度矩阵为 \({\bm C}\) , 则有

\[{\bm B} = {\bm C}^{-1}{\bm A}{\bm C} \]

提示

\[\begin{array}{l}T{\bm{x}} = T({{\bm{x}}_1},\;{{\bm{x}}_2}, \cdots ,{{\bm{x}}_n}) = ({{\bm{x}}_1},\;{{\bm{x}}_2}, \cdots ,{{\bm{x}}_n}){\bm{A}}\\T{\bm{y}} = T({{\bm{y}}_1},\;{{\bm{y}}_2}, \cdots ,{{\bm{y}}_n}) = ({{\bm{y}}_1},\;{{\bm{y}}_2}, \cdots ,{{\bm{y}}_n}){\bm{B}}\\T{\bm{y}} = T({{\bm{y}}_1},\;{{\bm{y}}_2}, \cdots ,{{\bm{y}}_n}) = T({{\bm{x}}_1},\;{{\bm{x}}_2}, \cdots ,{{\bm{x}}_n}){\bm{C}}\\\;\;\;\; = ({{\bm{x}}_1},\;{{\bm{x}}_2}, \cdots ,{{\bm{x}}_n}){\bm{AC}}{\rm{ = }}({{\bm{y}}_1},\;{{\bm{y}}_2}, \cdots ,{{\bm{y}}_n}){{\bm{C}}^{{\rm{ - }}1}}{\bm{AC}}\end{array} \]

相似矩阵¶

什么是相似矩阵¶

由线性变换在不同基下的矩阵关系引出矩阵相似定义:

Definition 1.10 (相似矩阵)

设有矩阵 \({\bm A}, {\bm B}\) , 若存在 非奇异矩阵 \({\bm P}\) 使得 \({\bm B} = {\bm P}^{-1}{\bm A}{\bm P}\) , 则称 \({\bm A}\) 相似于 \({\bm B}\) , 记作 \({\bm A} \sim {\bm B}\) .

警告

矩阵合同是指 \({\bm B} = {\bm P}^{T}{\bm A}{\bm P}\)

若 \({\bm B} = {\bm P}^{-1}{\bm A}{\bm P}\) , 且 \(f(t)\) 是数域 \(K\) 上的多项式, 则有

\[f({\bm B}) = {\bm P}^{-1} f({\bm A}) {\bm P} \]

性质¶

反身性: \(A \sim A\)
对称性: 若 \({\bm A} \sim {\bm B}\) , 则 \({\bm B} \sim {\bm A}\)
传递性: 若 \({\bm A} \sim {\bm B}, {\bm B} \sim {\bm C}\) , 则 \({\bm A} \sim {\bm C}\)

线性变换多项式的矩阵¶

数量 \(t\) 的 \(m\) 次多项式可以定义为

\[f(t) = a_m t^m + a_{m-1} t^{m-1} + \cdots + a_1t + a_0 \]

类似地, 线性空间 \({\mathbb V}^n\) 中，线性变换 \(T\) 的 \(m\) 次多项式可以定义为

\[f(T) = a_m T^m + a_{m-1} T^{m-1} + \cdots + a_1T + a_0 \]

设线性空间 \({\mathbb V}^n\) 中，线性变换 \(T\) 在基 \({\bm x}_1 , {\bm x}_2 , \cdots, {\bm x}_n\) 下的矩阵为 \({\bm A}\) , 即

\[T({\bm x}_1 , {\bm x}_2 , \cdots, {\bm x}_n) = ({\bm x}_1 , {\bm x}_2 , \cdots, {\bm x}_n){\bm A} \]

则 \(f(T)\) 在该基下的的矩阵 为

\[f({\bm A}) = a_m{\bm A}^m + a_{m-1}{\bm A}^{m-1} + \cdots + a_{1}{\bm A} + a_0{\bm I} \]

上式也称为方阵 \({\bm A}\) 的多项式.

常见线性变换¶

伸缩, 旋转, 对称变换举例

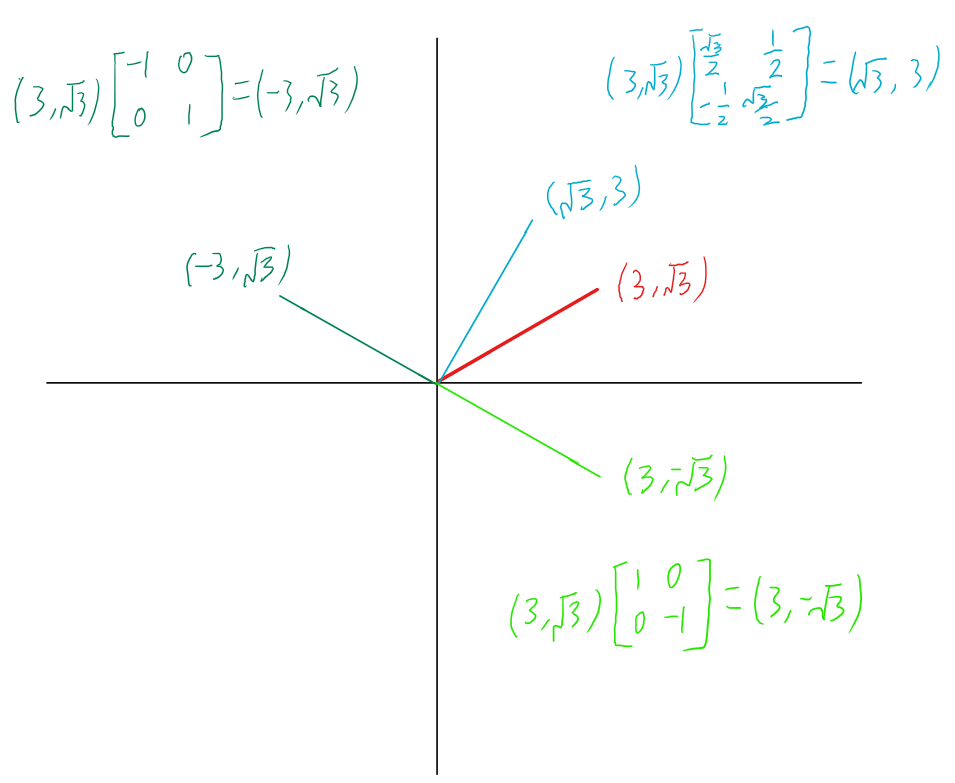
伸缩: \(\left[ {\begin{array}{rrr}k&0\\0&k\end{array}} \right]\left[ {\begin{array}{ccc}{{x_1}}\\{{x_2}}\end{array}} \right] = \left[ {\begin{array}{ccc}{k{x_1}}\\{k{x_2}}\end{array}} \right],\;\;\left[ {\begin{array}{rrr}{{k_1}}&0\\0&{{k_2}}\end{array}} \right]\left[ {\begin{array}{rrr}{{x_1}}\\{{x_2}}\end{array}} \right] = \left[ {\begin{array}{rrr}{{k_1}{x_1}}\\{{k_2}{x_2}}\end{array}} \right]\)
逆时针旋转: \(\left[ {\begin{array}{rrr}{\cos \theta }&{ - \sin \theta }\\{\sin \theta }&{\cos \theta }\end{array}} \right]\left[ {\begin{array}{ccc}{{x_1}}\\{{x_2}}\end{array}} \right] = \left[ {\begin{array}{ccc}{{x_1}\cos \theta - {x_2}\sin \theta }\\{{x_1}\sin \theta + {x_2}\cos \theta }\end{array}} \right]\)
顺时针旋转: \(\left[ {\begin{array}{rrr}{\cos \theta }&{\sin \theta }\\{ - \sin \theta }&{\cos \theta }\end{array}} \right]\left[ {\begin{array}{ccc}{{x_1}}\\{{x_2}}\end{array}} \right] = \left[ {\begin{array}{ccc}{{x_1}\cos \theta + {x_2}\sin \theta }\\{ - {x_1}\sin \theta + {x_2}\cos \theta }\end{array}} \right]\)
轴对称: \(\left[ {\begin{array}{rrr}1&0\\0&{ - 1}\end{array}} \right]\left[ {\begin{array}{ccc}{{x_1}}\\{{x_2}}\end{array}} \right] = \left[ {\begin{array}{ccc}{{x_1}}\\{ - {x_2}}\end{array}} \right],\;\;\left[ {\begin{array}{rrr}{ - 1}&0\\0&1\end{array}} \right]\left[ {\begin{array}{ccc}{{x_1}}\\{{x_2}}\end{array}} \right] = \left[ {\begin{array}{ccc}{ - {x_1}}\\{{x_2}}\end{array}} \right]\)

图 1.3 变换举例¶

变换举例, 伸缩, 旋转, 对称变换

提示

记忆旋转变换

逆时针旋转: 第一象限一个向量, 逆时针旋转一个小角度, \(x\) 坐标减小, \(y\) 坐标增大
顺时针旋转: 第一象限一个向量, 逆时针旋转一个小角度, \(x\) 坐标增大, \(y\) 坐标减小

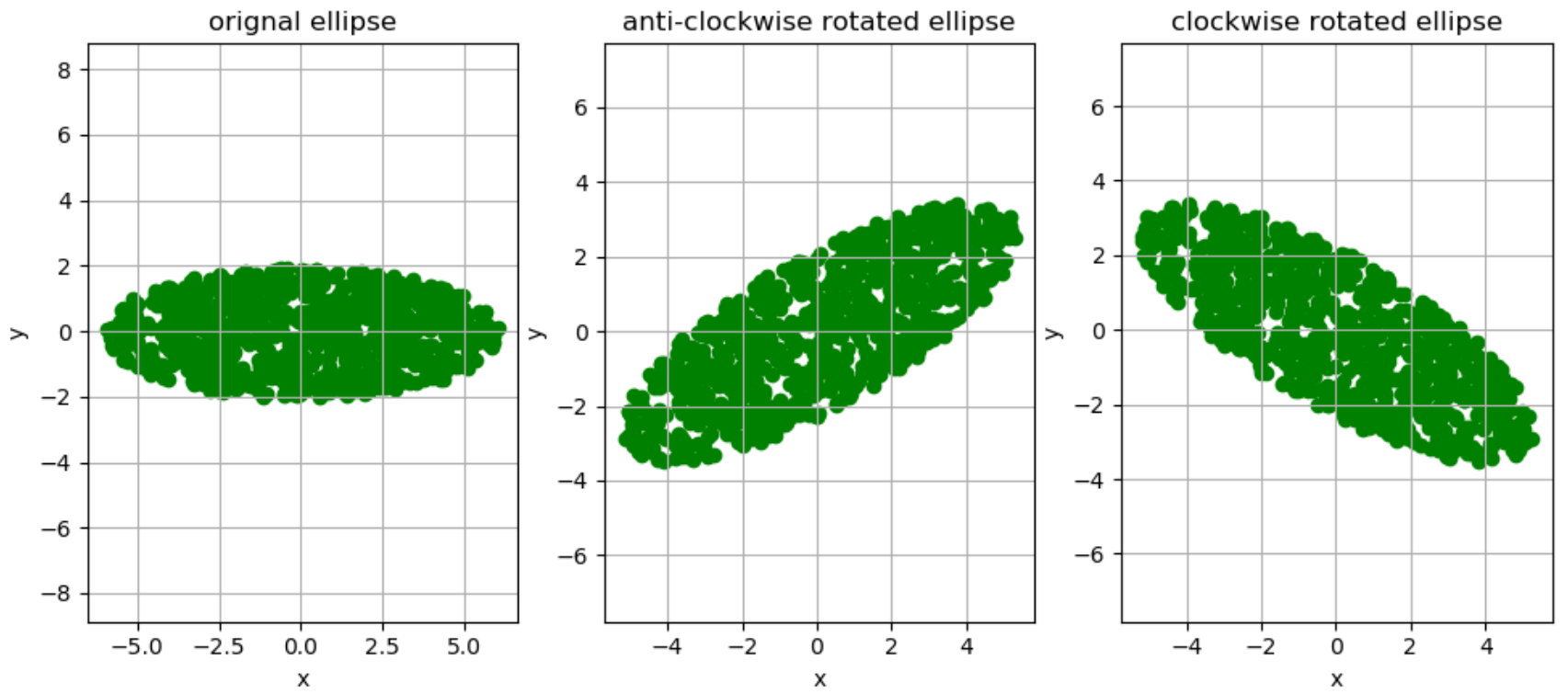
下面借助 Python 工具实现旋转变换的验证:

产生二维平面内椭圆内的随机点构成椭圆面 \(S\) ;
将椭圆面 \(S\) 分别进行逆时针与顺时针旋转;
绘制旋转前后的图像.

结果如下图

图 1.4 旋转变换举例.¶

旋转变换举例: 原始图(左), 逆时针旋转 \(30\) 度(中), 顺时针旋转 \(30\) 度(右).

实现代码, 参见文件 demo_rotation_ellipse.py .

代码 1.1 demo_rotation_ellipse.py¶

import pytool
import numpy as np
import matplotlib.pyplot as plt

# =====================generate Ellipse=====================
a = 6  # major axis
b = 2  # minor axis
x0 = 10  # center x0
y0 = 10  # center y0
N = 1000  # number of points

# angle for rotating ellipse data
theta = np.pi * 30 / 180

x, y = pytool.ellipse_surface(a, b, x0, y0, N, 'rand')

x = x - np.mean(x)
y = y - np.mean(y)

xy = np.array([x, y])
print(xy.shape)

A = xy

# ========================rotate============================
# ------------rotating matrix(Anti-clockwise)------------
M1 = [[np.cos(theta), -np.sin(theta)],
      [np.sin(theta), np.cos(theta)]]
print("M1", M1)

# -----------------------rotating--------
A1 = np.dot(M1, A)

x1 = A1[0]
y1 = A1[1]

# ------------rotating matrix(clockwise)-----------------
M2 = [[np.cos(theta), np.sin(theta)],
      [-np.sin(theta), np.cos(theta)]]
print("M2", M2)

# -----------------------rotating--------
A2 = np.dot(M2, A)

x2 = A2[0]
y2 = A2[1]

# ========================show data=========================
xmin = np.min([x, x1, x2])
xmax = np.max([x, x1, x2])
ymin = np.min([y, y1, y2])
ymax = np.max([y, y1, y2])
plt.figure()
plt.subplot(131)
plt.scatter(x, y, c='g', marker='o')
plt.grid()
plt.axis([xmin, xmax, ymin, ymax])
# plt.axis('equal')
plt.xlabel('x')
plt.ylabel('y')
plt.title('orignal ellipse')
plt.subplot(132)
plt.scatter(x1, y1, c='g', marker='o')
plt.grid()
plt.axis([xmin, xmax, ymin, ymax])
# plt.axis('equal')
plt.xlabel('x')
plt.ylabel('y')
plt.title('anti-clockwise rotated ellipse')
plt.subplot(133)
plt.scatter(x2, y2, c='g', marker='o')
plt.grid()
plt.axis([xmin, xmax, ymin, ymax])
# plt.axis('equal')
plt.xlabel('x')
plt.ylabel('y')
plt.title('clockwise rotated ellipse')
plt.show()

1.3.4. 总结¶

线性变换对向量组相关性的影响 - 线性相关向量组 –> 线性变换 –> 线性相关 - 线性无关向量组 –> 线性变换 –> 线性无关或线性相关（如零变换）
线性变换 \(T\) 与其对应矩阵 \(A\) - 它们的值域、核、秩、亏相同