4.2. 三角分解¶

三角分解 ( Triangular Decomposition ) 是把一个矩阵 \({\bm A}_{n\times n}\) 分解为一个下三角矩阵 ( Lower Triangular Matrix ) \({\bm L}\) 与一个上三角矩阵 ( Upper Triangular Matrix ) \({\bm U}\) 乘积的分解, 也可分解为一个单位下三角矩阵 ( Unit Lower Triangular Matrix ) \({\bm L}\) 与一个对角阵 ( Diagonal Matrix ) \({\bm D}\) 及一个单位上三角矩阵 ( Unit Upper Triangular Matrix ) \({\bm U}\) 乘积.

Definition 4.1 (三角分解)

称满足如下形式的矩阵分解为 三角分解 :

\[{\bm A}_{n\times n} = {\bm L}_{n\times n} {\bm U}_{n\times n} \]

\[{\bm A}_{n\times n} = {\bm L}_{n\times n} {\bm D}_{n\times n} {\bm U}_{n\times n} \]

4.2.1. 引言¶

考虑方程组 \({\bm A}{\bm x} = {\bm b}\) , 即

\[\left[ {\begin{array}{llll} {{a_{11}}}&{{a_{12}}}& \cdots &{{a_{1n}}}\\ {{a_{21}}}&{{a_{22}}}& \cdots &{{a_{2n}}}\\ \vdots & \vdots & \ddots & \vdots \\ {{a_{n1}}}&{{a_{n2}}}& \cdots &{{a_{nn}}} \end{array}} \right]\left[ {\begin{array}{l} {{x_1}}\\ {{x_2}}\\ \vdots \\ {{x_n}} \end{array}} \right] = \left[ {\begin{array}{l} {{a_{11}}{x_1} + {a_{12}}{x_2} + \cdots + {a_{1n}}{x_n}}\\ {{a_{21}}{x_1} + {a_{22}}{x_2} + \cdots + {a_{2n}}{x_n}}\\ \vdots \\ {{a_{n1}}{x_1} + {a_{n2}}{x_2} + \cdots + {a_{nn}}{x_n}} \end{array}} \right] = \left[ {\begin{array}{l} {{b_1}}\\ {{b_2}}\\ \vdots \\ {{b_n}} \end{array}} \right] \]

若 \({\bm A}\) 为下三角矩阵, 则有

\[\left[ {\begin{array}{llll} {{a_{11}}}&0& \cdots &0\\ {{a_{21}}}&{{a_{22}}}& \cdots &0\\ \vdots & \vdots & \ddots & \vdots \\ {{a_{n1}}}&{{a_{n2}}}& \cdots &{{a_{nn}}} \end{array}} \right]\left[ {\begin{array}{l} {{x_1}}\\ {{x_2}}\\ \vdots \\ {{x_n}} \end{array}} \right] = \left[ {\begin{array}{l} {{a_{11}}{x_1}}\\ {{a_{21}}{x_1} + {a_{22}}{x_2}}\\ {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots }\\ {{a_{n1}}{x_1} + {a_{n2}}{x_2} + \cdots + {a_{nn}}{x_n}} \end{array}} \right] = \left[ {\begin{array}{l} {{b_1}}\\ {{b_2}}\\ \vdots \\ {{b_n}} \end{array}} \right] \]

若 \({\bm A}\) 为上三角矩阵, 则有

\[\left[ {\begin{array}{llll} {{a_{11}}}&{{a_{12}}}& \cdots &{{a_{1n}}}\\ 0&{{a_{22}}}& \cdots &{{a_{2n}}}\\ \vdots & \vdots & \ddots & \vdots \\ 0&0& \cdots &{{a_{nn}}} \end{array}} \right]\left[ {\begin{array}{c} {{x_1}}\\ {{x_2}}\\ \vdots \\ {{x_n}} \end{array}} \right] = \left[ {\begin{array}{r} {{a_{11}}{x_1} + {a_{12}}{x_2} + \cdots + {a_{1n}}{x_n}}\\ {{a_{22}}{x_2} + \cdots + {a_{2n}}{x_n}}\\ { \vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;}\\ {{a_{nn}}{x_n}} \end{array}} \right] = \left[ {\begin{array}{c} {{b_1}}\\ {{b_2}}\\ \vdots \\ {{b_n}} \end{array}} \right] \]

可见当 \({\bm A}\) 为下三角矩阵或上三角矩阵时, 方程组可以很容易求解. 下面设法将 \({\bm A}\) 化为上/下三角矩阵.

4.2.2. 高斯消元过程¶

一般消元过程¶

以上三角矩阵为例, 记 \({\bm A}^{(1)} = A\) , 且 \({\bm A}^{(k)}_{ij} = a^{(k)}_{ij}\) 采用初等行变换:

将 \({\bm A}^{(1)}\) 的第1列元素除第一个元素 \(a^{(1)}_{11}\) 外, 其余元素都化为 \(0\) , 显然若 \(a^{(1)}_{11} \neq 0\) , 可以分别以 \(-\frac{a^{(1)}_{21}}{a^{(1)}_{11}}, -\frac{a^{(1)}_{31}}{a^{(1)}_{11}}, \cdots, -\frac{a^{(1)}_{n1}}{a^{(1)}_{11}}\) 乘以第 \(1\) 行元素, 分别加到第 \(2, 3, \cdots, n\) 行得

\[{\bm A}^{(1)} = \left[ {\begin{array}{ccccc} {{a^{(1)}_{11}}}&{{a^{(1)}_{12}}}&{{a^{(1)}_{13}}}& \cdots &{{a^{(1)}_{1n}}}\\ {{a^{(1)}_{21}}}&{{a^{(1)}_{22}}}&{{a^{(1)}_{23}}}& \cdots &{{a^{(1)}_{2n}}}\\ {{a^{(1)}_{31}}}&{{a^{(1)}_{32}}}&{{a^{(1)}_{33}}}& \cdots &{{a^{(1)}_{3n}}}\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ {{a^{(1)}_{n1}}}&{{a^{(1)}_{n2}}}&{{a^{(1)}_{n3}}}& \cdots &{{a^{(1)}_{nn}}} \end{array}} \right] \mathop {\mathop \to \limits_{i = 2, \cdots ,n} }\limits^{{r_i} - \frac{{{a^{(1)}_{i1}}}}{{{a^{(1)}_{11}}}}{r_1}} \]

\[{\bm A}^{(2)} = \left[ {\begin{array}{lllll} {{a^{(1)}_{11}}}&{{a^{(1)}_{12}}}&{{a^{(1)}_{13}}}& \cdots &{{a^{(1)}_{1n}}}\\ 0&{{a^{(1)}_{22}} - \frac{{{a^{(1)}_{21}}{a^{(1)}_{12}}}}{{{a^{(1)}_{11}}}}}&{{a^{(1)}_{23}} - \frac{{{a^{(1)}_{21}}{a^{(1)}_{13}}}}{{{a^{(1)}_{11}}}}}& \cdots &{{a^{(1)}_{2n}} - \frac{{{a^{(1)}_{21}}{a^{(1)}_{1n}}}}{{{a^{(1)}_{11}}}}}\\ 0&{{a^{(1)}_{32}} - \frac{{{a^{(1)}_{31}}{a^{(1)}_{12}}}}{{{a^{(1)}_{11}}}}}&{{a^{(1)}_{33}} - \frac{{{a^{(1)}_{31}}{a^{(1)}_{13}}}}{{{a^{(1)}_{11}}}}}& \cdots &{{a^{(1)}_{3n}} - \frac{{{a^{(1)}_{31}}{a^{(1)}_{1n}}}}{{{a^{(1)}_{11}}}}}\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0&{{a^{(1)}_{n2}} - \frac{{{a^{(1)}_{n1}}{a^{(1)}_{12}}}}{{{a^{(1)}_{11}}}}}&{{a^{(1)}_{n3}} - \frac{{{a^{(1)}_{n1}}{a^{(1)}_{13}}}}{{{a^{(1)}_{11}}}}}& \cdots &{{a^{(1)}_{nn}} - \frac{{{a^{(1)}_{n1}}{a^{(1)}_{1n}}}}{{{a^{(1)}_{11}}}}} \end{array}} \right] \]

若记 \(\left({\bm L}^{(1)}_{i1}\right)^{(-1)} = l^{(1)}_{i1} = -\frac{a^{(1)}_{i1}}{a^{(1)}_{11}}\) , \({\bm L}^{(1)}_{i1} = l^{(1)}_{i1} = \frac{a^{(1)}_{i1}}{a^{(1)}_{11}}\) , 即

\[{\left( {{\bm{L}}^{(1)}} \right)^{ - 1}} = \left[ {\begin{array}{ccccc} 1&0&0& \cdots &0\\ { - \frac{{{a^{(1)}_{21}}}}{{{a^{(1)}_{11}}}}}&1&0& \cdots &0\\ { - \frac{{{a^{(1)}_{31}}}}{{{a^{(1)}_{11}}}}}&0&1& \cdots &0\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ { - \frac{{{a^{(1)}_{n1}}}}{{{a^{(1)}_{11}}}}}&0&0& \cdots &1 \end{array}} \right],\;\;{\bm{L}}^{(1)} = \left[ {\begin{array}{ccccc} 1&0&0& \cdots &0\\ {\frac{{{a^{(1)}_{21}}}}{{{a^{(1)}_{11}}}}}&1&0& \cdots &0\\ {\frac{{{a^{(1)}_{31}}}}{{{a^{(1)}_{11}}}}}&0&1& \cdots &0\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ {\frac{{{a^{(1)}_{n1}}}}{{{a^{(1)}_{11}}}}}&0&0& \cdots &1 \end{array}} \right] \]

则有

\[{{\bm{A}}^{(2)}} = {\left( {{\bm{L}}^{(1)}} \right)^{ - 1}}{{\bm{A}}^{(1)}} = \left[ {\begin{array}{ccccc} {a_{11}^{(2)}}&{a_{12}^{(2)}}&{a_{13}^{(2)}}& \cdots &{a_{1n}^{(2)}}\\ 0&{a_{22}^{(2)}}&{a_{23}^{(2)}}& \cdots &{a_{2n}^{(2)}}\\ 0&{a_{32}^{(2)}}&{a_{33}^{(2)}}& \cdots &{a_{3n}^{(2)}}\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0&{a_{n2}^{(2)}}&{a_{n3}^{(2)}}& \cdots &{a_{nn}^{(2)}} \end{array}} \right] = \left[ {\begin{array}{ccccc} {a_{11}^{(1)}}&{a_{12}^{(1)}}&{a_{13}^{(1)}}& \cdots &{a_{1n}^{(1)}}\\ 0&{a_{22}^{(2)}}&{a_{23}^{(2)}}& \cdots &{a_{2n}^{(2)}}\\ 0&{a_{32}^{(2)}}&{a_{33}^{(2)}}& \cdots &{a_{3n}^{(2)}}\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0&{a_{n2}^{(2)}}&{a_{n3}^{(2)}}& \cdots &{a_{nn}^{(2)}} \end{array}} \right] \]

将 \({\bm A}^{(2)}\) 的第2列元素除前2个元素 \(a^{(2)}_{12}, a^{(2)}_{22}\) 外, 其余元素都化为 \(0\) , 显然若 \(a^{(2)}_{22} \neq 0\) , 可以分别以 \(-\frac{a^{(2)}_{32}}{a^{(2)}_{22}}, -\frac{a^{(2)}_{42}}{a^{(2)}_{22}}, \cdots, -\frac{a^{(2)}_{n2}}{a^{(2)}_{22}}\) 乘以第 \(2\) 行元素, 分别加到第 \(3, \cdots, n\) 行得

\[{\bm A}^{(2)} = \left[ {\begin{array}{ccccc} {a_{11}^{(2)}}&{a_{12}^{(2)}}&{a_{13}^{(2)}}& \cdots &{a_{1n}^{(2)}}\\ 0&{a_{22}^{(2)}}&{a_{23}^{(2)}}& \cdots &{a_{2n}^{(2)}}\\ 0&{a_{32}^{(2)}}&{a_{33}^{(2)}}& \cdots &{a_{3n}^{(2)}}\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0&{a_{n2}^{(2)}}&{a_{n3}^{(2)}}& \cdots &{a_{nn}^{(2)}} \end{array}} \right]\mathop {\mathop \to \limits_{i = 3, \cdots ,n} }\limits^{{r_i} - \frac{{a_{i2}^{(2)}}}{{a_{22}^{(2)}}}{r_2}} \]

\[{{\bm{A}}^{(3)}} = \left[ {\begin{array}{lllll} {a_{11}^{(2)}}&{a_{12}^{(2)}}&{a_{13}^{(2)}}& \cdots &{a_{1n}^{(2)}}\\ 0&{a_{22}^{(2)}}&{a_{23}^{(2)}}& \cdots &{a_{2n}^{(2)}}\\ 0&0&{a_{33}^{(2)} - \frac{{a_{32}^{(2)}a_{23}^{(2)}}}{{a_{22}^{(2)}}}}& \cdots &{a_{3n}^{(2)} - \frac{{a_{32}^{(2)}a_{2n}^{(2)}}}{{a_{22}^{(2)}}}}\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0&0&{a_{n3}^{(2)} - \frac{{a_{n2}^{(2)}a_{23}^{(2)}}}{{a_{22}^{(2)}}}}& \cdots &{a_{nn}^{(2)} - \frac{{a_{n2}^{(2)}a_{2n}^{(2)}}}{{a_{22}^{(2)}}}} \end{array}} \right] \]

若记 \(\left({\bm L}^{(2)}_{i2}\right)^{(-1)} = l^{(2)}_{i2} = -\frac{a^{(2)}_{i2}}{a^{(2)}_{22}}\) , \({\bm L}^{(2)}_{i2} = l^{(2)}_{i2} = \frac{a^{(2)}_{i2}}{a^{(2)}_{22}}\) , 即

\[{\left( {{{\bm{L}}^{(2)}}} \right)^{ - 1}} = \left[ {\begin{array}{ccccc} 1&0&0& \cdots &0\\ 0&1&0& \cdots &0\\ 0&{ - \frac{{a_{32}^{(2)}}}{{a_{22}^{(2)}}}}&1& \cdots &0\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0&{ - \frac{{a_{n2}^{(2)}}}{{a_{22}^{(2)}}}}&0& \cdots &1 \end{array}} \right],\;\;{{\bm{L}}^{(2)}} = \left[ {\begin{array}{ccccc} 1&0&0& \cdots &0\\ 0&1&0& \cdots &0\\ 0&{\frac{{a_{32}^{(2)}}}{{a_{22}^{(2)}}}}&1& \cdots &0\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0&{\frac{{a_{n2}^{(2)}}}{{a_{22}^{(2)}}}}&0& \cdots &1 \end{array}} \right] \]

则有

\[{{\bm{A}}^{(3)}} = {\left( {{{\bm{L}}^{(2)}}} \right)^{ - 1}}{{\bm{A}}^{(2)}} = \left[ {\begin{array}{ccccc} {a_{11}^{(3)}}&{a_{12}^{(3)}}&{a_{13}^{(3)}}& \cdots &{a_{1n}^{(3)}}\\ 0&{a_{22}^{(3)}}&{a_{23}^{(3)}}& \cdots &{a_{2n}^{(3)}}\\ 0&0&{a_{33}^{(3)}}& \cdots &{a_{3n}^{(3)}}\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0&0&{a_{n3}^{(3)}}& \cdots &{a_{nn}^{(3)}} \end{array}} \right] = \left[ {\begin{array}{ccccc} {a_{11}^{(1)}}&{a_{12}^{(1)}}&{a_{13}^{(1)}}& \cdots &{a_{1n}^{(1)}}\\ 0&{a_{22}^{(2)}}&{a_{23}^{(2)}}& \cdots &{a_{2n}^{(2)}}\\ 0&0&{a_{33}^{(3)}}& \cdots &{a_{3n}^{(3)}}\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0&0&{a_{n3}^{(3)}}& \cdots &{a_{nn}^{(3)}} \end{array}} \right] \]

重复如上步骤, 最终可将矩阵 \({\bm A}\) 化为上三角矩阵.

\[{{\bm{A}}^{(n)}} = {\left( {{{\bm{L}}^{(n - 1)}}} \right)^{ - 1}}{{\bm{A}}^{(n - 1)}} = \left[ {\begin{array}{ccccc} {a_{11}^{(n)}}&{a_{12}^{(n)}}&{a_{13}^{(n)}}& \cdots &{a_{1n}^{(n)}}\\ 0&{a_{22}^{(n)}}&{a_{23}^{(n)}}& \cdots &{a_{2n}^{(n)}}\\ 0&0&{a_{33}^{(n)}}& \cdots &{a_{3n}^{(n)}}\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0&0&0& \cdots &{a_{nn}^{(n)}} \end{array}} \right] = \left[ {\begin{array}{ccccc} {a_{11}^{(1)}}&{a_{12}^{(1)}}&{a_{13}^{(1)}}& \cdots &{a_{1n}^{(1)}}\\ 0&{a_{22}^{(2)}}&{a_{23}^{(2)}}& \cdots &{a_{2n}^{(2)}}\\ 0&0&{a_{33}^{(3)}}& \cdots &{a_{3n}^{(3)}}\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0&0&0& \cdots &{a_{nn}^{(n)}} \end{array}} \right] \]

警告

上述消元过程可以执行的充要条件是矩阵 \({\bm A}\) 的各阶顺序主子式不为零, 即

\[\Delta_k = a_{11}^{(1)} a_{22}^{(2)} \cdots a_{kk}^{(k)} \neq 0, (k = 1, 2, \cdots, n). \]

主元素选取¶

若矩阵 \({\bm A}\) 的各阶顺序主子式不全为零, 则可以通过选取主元素进行消元, 核心思想是通过初等变换, 使得矩阵的顺序主子式不为零, 主元素选取包含:

列主元素法: 在矩阵的某列中选取模值最大的作为新的对角元素, 选取范围为对角线元素以下的各元素.
行主元素法: 在矩阵的某行中选取模值最大的作为新的对角元素, 选取范围为对角线元素以后的各元素.
全主元素法: 若某列元素均较小或某行元素均较小时, 可在各行各列中选取模值最大者作为对角元素.

此时, 可以通过初等变换 \({\bm P}\) 将矩阵 \({\bm A}\) 变为各阶顺序主子式不为零等矩阵 \({\bm{PA}}\) (行) \({\bm{AP}}\) (列).

注解

如对于矩阵

\[{\bm A} = \left[ {\begin{array}{ccc} 0&2&2\\ 2&1&2\\ 0&2&1 \end{array}} \right] \]

易知 \(\Delta_1 = 0\)

采用列主元素法, 选取 \(a_{21} = 2\) 作为主元素, 即交换前两行, 记对应初等变换为 \({\bm P}_1\) , 则

\[{{\bm{P}}_1}{\bm{A}} = \left[ {\begin{array}{ccc} 0&1&0\\ 1&0&0\\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{ccc} 0&2&2\\ 2&1&2\\ 0&2&1 \end{array}} \right] = \left[ {\begin{array}{ccc} 2&1&2\\ 0&2&2\\ 0&2&1 \end{array}} \right] \]

采用行主元素法, 选取 \(a_{12} = 2\) 作为主元素, 即交换前两列, 记对应初等变换为 \({\bm P}_2\) , 则

\[{\bm{A}}{{\bm{P}}_2} = \left[ {\begin{array}{ccc} 0&2&2\\ 2&1&2\\ 0&2&1 \end{array}} \right]\left[ {\begin{array}{ccc} 0&1&0\\ 1&0&0\\ 0&0&1 \end{array}} \right] = \left[ {\begin{array}{ccc} 2&0&2\\ 1&2&2\\ 2&0&1 \end{array}} \right] \]

4.2.3. 变元求解¶

假设矩阵 \({\bm A}\) 可以分解为下三角矩阵 \({\bm L}\) 与上三角矩阵 \({\bm U}\) 的乘积, 即

\[\left[ {\begin{array}{cccc} {{a_{11}}}&{{a_{12}}}& \ldots &{{a_{1n}}}\\ {{a_{21}}}&{{a_{22}}}& \cdots &{{a_{2n}}}\\ \vdots & \vdots & \vdots & \vdots \\ {{a_{n1}}}&{{a_{n2}}}& \cdots &{{a_{nn}}} \end{array}} \right] = \left[ {\begin{array}{cccc} {{l_{11}}}&{}&{}&{}\\ {{l_{21}}}&{{l_{22}}}&{}&{}\\ \vdots & \vdots & \ddots &{}\\ {{l_{n1}}}&{{l_{n2}}}& \cdots &{{l_{nn}}} \end{array}} \right]\left[ {\begin{array}{cccc} {{u_{11}}}&{{u_{12}}}& \cdots &{{u_{1n}}}\\ {}&{{u_{22}}}& \cdots &{{u_{2n}}}\\ {}&{}& \ddots & \vdots \\ {}&{}&{}&{{u_{nn}}} \end{array}} \right] \]

则可得以下方程组

\[\left\{ {\begin{array}{l} {{a_{11}} = {l_{11}}{u_{11}}}\\ {{a_{12}} = {l_{11}}{u_{12}}}\\ \vdots \\ {{a_{1n}} = {l_{11}}{u_{1n}}} \end{array}} \right.,\;\;\left\{ {\begin{array}{l} {{a_{21}} = {l_{21}}{u_{11}}}\\ {{a_{22}} = {l_{21}}{u_{12}} + {l_{22}}{u_{22}}}\\ {\;\;\;\;\;\; \vdots }\\ {{a_{2n}} = {l_{21}}{u_{1n}} + {l_{22}}{u_{2n}}} \end{array}} \right.,\; \cdots ,\;\left\{ {\begin{array}{l} {{a_{n1}} = {l_{n1}}{u_{11}}}\\ {{a_{n2}} = {l_{n1}}{u_{12}} + {l_{n2}}{u_{22}}}\\ {\;\;\;\;\;\; \vdots }\\ {{a_{nn}} = {l_{n1}}{u_{1n}} + {l_{n2}}{u_{2n}} + \cdots + {l_{nn}}{u_{nn}}} \end{array}} \right. \]

观察易知上述方程组没有唯一解, 而当 \({\bm L}\) 为单位下三角矩阵时( \(l_{11} = l_{22} = \cdots l_{nn} = 1\) ) 或当 \({\bm U}\) 为单位上三角矩阵时( \(u_{11} = u_{22} = \cdots u_{nn} = 1\) ) , 方程组有唯一解.

提示

如对于二阶矩阵, 显然有

\[\left[ {\begin{array}{cc} {{a_{11}}}&{{a_{12}}}\\ {{a_{21}}}&{{a_{22}}} \end{array}} \right] = \left[ {\begin{array}{cc} {{l_{11}}}&{}\\ {{l_{21}}}&{{l_{22}}} \end{array}} \right]\left[ {\begin{array}{cc} {{u_{11}}}&{{u_{12}}}\\ {}&{{u_{22}}} \end{array}} \right] = \left[ {\begin{array}{cc} {{l_{11}}{u_{11}}}&{{l_{11}}{u_{12}}}\\ {{l_{21}}{u_{11}}}&{{l_{22}}{u_{22}}} \end{array}} \right] \]

得方程组

\[\left\{ {\begin{array}{ll} {{a_{11}} = {l_{11}}{u_{11}}}\\ {{a_{12}} = {l_{11}}{u_{12}}}\\ {{a_{21}} = {l_{21}}{u_{11}}}\\ {{a_{22}} = {l_{21}}{u_{12}} + {l_{22}}{u_{22}}} \end{array}} \right. \]

上述方程组显然没有唯一解, 故分解不唯一, 而当 \({\bm L}\) 为单位下三角矩阵时( \(l_{11} = l_{22} = 1\) ) 或当 \({\bm U}\) 为单位上三角矩阵时( \(u_{11} = u_{22} = 1\) ) , 方程组有唯一解. 即

\[{\bm{L}} = \left[ {\begin{array}{cc} 1&{}\\ {\frac{{{a_{21}}}}{{{a_{11}}}}}&1 \end{array}} \right],\;{\bm{U}} = \left[ {\begin{array}{cc} {{a_{11}}}&{{a_{12}}}\\ {}&{{a_{22}} - \frac{{{a_{21}}{a_{12}}}}{{{a_{11}}}}} \end{array}} \right] \]

或者

\[{\bm{L}} = \left[ {\begin{array}{cc} {{a_{11}}}&{}\\ {{a_{21}}}&{{a_{22}} - \frac{{{a_{21}}{a_{12}}}}{{{a_{11}}}}} \end{array}} \right],\;{\bm{U}} = \left[ {\begin{array}{cc} 1&{\frac{{{a_{12}}}}{{{a_{11}}}}}\\ {}&1 \end{array}} \right] \]

4.2.4. LU分解与LDU分解¶

概念与性质¶

如上所述, 易知

\[{\bm{A}} = {{\bm{A}}^{(1)}} = {{\bm{L}}^{(1)}}{{\bm{A}}^{(2)}} = {{\bm{L}}^{(1)}}{{\bm{L}}^{(2)}}{{\bm{A}}^{(3)}} = \cdots = {{\bm{L}}^{(1)}}{{\bm{L}}^{(2)}} \cdots {{\bm{L}}^{(n - 1)}}{{\bm{A}}^{(n)}} \]

容易求得

\[{\bm{L}} = {{\bm{L}}^{(1)}}{{\bm{L}}^{(2)}} \cdots {{\bm{L}}^{(n - 1)}} = \left[ {\begin{array}{ccccc} 1&{}&{}&{}&{}\\ {{l_{21}}}&1&{}&{}&{}\\ {{l_{31}}}&{{l_{32}}}&1&{}&{}\\ \vdots & \vdots & \cdots & \ddots &{}\\ {{l_{n1}}}&{{l_{n2}}}&{{l_{n3}}}& \cdots &1 \end{array}} \right] \]

令 \({\bm U} = {\bm A}^{(n)}\) , 则有 LU分解

\[{\bm{A}} = {\bm{LU}} \]

其中:

\({\bm L}^{(1)}, {\bm L}^{(2)}, \cdots, {\bm L}^{(n-1)}\) 称为 Frobenius 矩阵
\({l_{ij}} = \frac{{a_{ij}^{(j)}}}{{a_{jj}^{(j)}}}, j < i\)
\({\bm L}\) 为下三角矩阵
\({\bm U}\) 为上三角矩阵
\({\bm L}{\bm U}\) 分解一般不唯一, 当 \({\bm L}\) 为单位下三角矩阵, 或者 \({\bm U}\) 为单位上三角矩阵时, \({\bm L}{\bm U}\) 分解唯一

若矩阵 \({\bm A}\) 可以分解为单位下三角矩阵 \({\bm L}\) 和单位上三角矩阵 \({\bm U}\) 和对角矩阵 \({\bm D}\) 的乘积, 即

\[{\bm A}_{n\times n} = {\bm L}_{n\times n} {\bm D}_{n\times n} {\bm U}_{n\times n} \]

则称上述分解为矩阵 \({\bm A}\) 的 \({\bm L}{\bm D}{\bm U}\) 分解.

其中 \({\bm D} = {\rm diag}(d_1, d_2, \cdots, d_n)\) 为对角元素不为零的 \(n\) 阶对角阵, 且 \(d_k=\frac{\Delta_k}{\Delta_{k-1}}\) , \(k=1,2,\cdots, n\) , \(\Delta_k\) 为 \({\bm A}\) 的 \(k\) 阶顺序主子式, 且规定 \(\Delta_0=1\) .

提示

\(n\) 阶非奇异矩阵 \({\bm A}\) 有三角分解 LU 或 LDU 的充要条件是 \({\bm A}\) 的顺序主子式 \(\Delta_k \neq 0, (k=1,2,\cdots, n)\) ;
对于任意可逆矩阵 \({\bm A}\) , 存在置换矩阵 \({\bm P}\) 使得 \({\bm P}{\bm A}\) 的所有顺序主子式全不为零.

计算方法¶

方法1: 高斯消元法
方法2: 变元求解法

高斯消元法¶

高斯消元法: 采用上述消元过程求解即可, 若矩阵 \({\bm A}\) 的各阶顺序主子式不全为零, 则可以通过选取主元素进行消元.

注解

举个例子: 求如下矩阵的 \({\bm L}{\bm U}\) 和 \({\bm L}{\bm D}{\bm U}\) 分解

\[{\bm A} = \left[ {\begin{array}{ccc} 0&2&2\\ 2&1&2\\ 0&2&1 \end{array}} \right] \]

解: 采用列主元素法, 选取 \(a_{21} = 2\) 作为主元素, 即交换前两行, 记对应初等变换为 \({\bm P}_1\) , 则

\[{\bm A}^{(2)} = {{\bm{P}}_1}{\bm{A}} = \left[ {\begin{array}{ccc} 0&1&0\\ 1&0&0\\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{ccc} 0&2&2\\ 2&1&2\\ 0&2&1 \end{array}} \right] = \left[ {\begin{array}{ccc} 2&1&2\\ 0&2&2\\ 0&2&1 \end{array}} \right] \]

对上述矩阵进行消元, 可见 \({\bm A}^{(2)}\) 的第一列除对角元素外, 其它均为零, 无需进行消元, 下面对 \({\bm A}^{(2)}\) 的第2列进行消元, 有

\[{\left( {{{\bm{L}}^{{\rm{(2)}}}}} \right)^{{\rm{ - }}1}}{\rm{ = }}\left[ {\begin{array}{ccc} 1&0&0\\ 0&1&0\\ 0&{{\rm{ - }}1}&1 \end{array}} \right]{\rm{,}}\;{{\bm{L}}^{{\rm{(2)}}}}{\rm{ = }}\left[ {\begin{array}{ccc} 1&0&0\\ 0&1&0\\ 0&1&1 \end{array}} \right]{\rm{,}}\;{\bm{L}}_{32}^{(2)} = l_{32}^{(2)} = - \frac{{a_{32}^{(2)}}}{{a_{22}^{(2)}}} = - 1 \]

\[{\left( {{{\bm{L}}^{({\rm{2}})}}} \right)^{{\rm{ - }}1}}{{\bm{A}}^{(2)}}{\rm{ = }}\left[ {\begin{array}{ccc} 1&0&0\\ 0&1&0\\ 0&{{\rm{ - }}1}&1 \end{array}} \right]\left[ {\begin{array}{ccc} 2&1&2\\ 0&2&2\\ 0&2&1 \end{array}} \right]{\rm{ = }}\left[ {\begin{array}{ccc} 2&1&2\\ 0&2&2\\ 0&0&{{\rm{ - }}1} \end{array}} \right] = {{\bm{A}}^{(3)}} \]

至此已将矩阵 \({\bm A}\) 转为上三角矩阵, 且 \({\bm{A}} = {\bm{P}}_1^{ - 1}{{\bm{A}}^{(2)}} = {\bm{P}}_1^{ - 1}{{\bm{L}}^{({\rm{2}})}}{{\bm{A}}^{(3)}}\)

对于 \({\bm A}={\bm{LU}}\) 分解, 有

\[{\bm{L}} = {\bm{P}}_1^{ - 1}{{\bm{L}}^{({\rm{2}})}} = \left[ {\begin{array}{ccc} 0&1&0\\ 1&0&0\\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{ccc} 1&0&0\\ 0&1&0\\ 0&1&1 \end{array}} \right] = \left[ {\begin{array}{ccc} 0&1&0\\ 1&0&0\\ 0&1&1 \end{array}} \right], \]

\[{\bm{U}} = {{\bm{A}}^{(3)}} = \left[ {\begin{array}{ccc} 2&1&2\\ 0&2&2\\ 0&0&{{\rm{ - }}1} \end{array}} \right] \]

对于 \({\bm A}={\bm{LDU}}\) 分解, 有

\[{\bm{L}} = {\bm{P}}_1^{ - 1}{{\bm{L}}^{({\rm{2}})}} = \left[ {\begin{array}{ccc} 0&1&0\\ 1&0&0\\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{ccc} 1&0&0\\ 0&1&0\\ 0&1&1 \end{array}} \right] = \left[ {\begin{array}{ccc} 0&1&0\\ 1&0&0\\ 0&1&1 \end{array}} \right], \]

\[{\bm{D}} = \left[ {\begin{array}{ccc} 2&{}&{}\\ {}&2&{}\\ {}&{}&{ - 1} \end{array}} \right],\;{\bm{U}} = \left[ {\begin{array}{ccc} 1&{1/2}&1\\ 0&1&1\\ 0&0&1 \end{array}} \right] \]

则

\[{\bm{A}} = {\bm{LDU}} = \left[ {\begin{array}{ccc} 0&1&0\\ 1&0&0\\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{ccc} 2&{}&{}\\ {}&2&{}\\ {}&{}&{ - 1} \end{array}} \right]\left[ {\begin{array}{ccc} 1&{1/2}&1\\ 0&1&1\\ 0&0&1 \end{array}} \right] = \left[ {\begin{array}{ccc} 0&2&2\\ 2&1&2\\ 0&2&1 \end{array}} \right] \]

提示

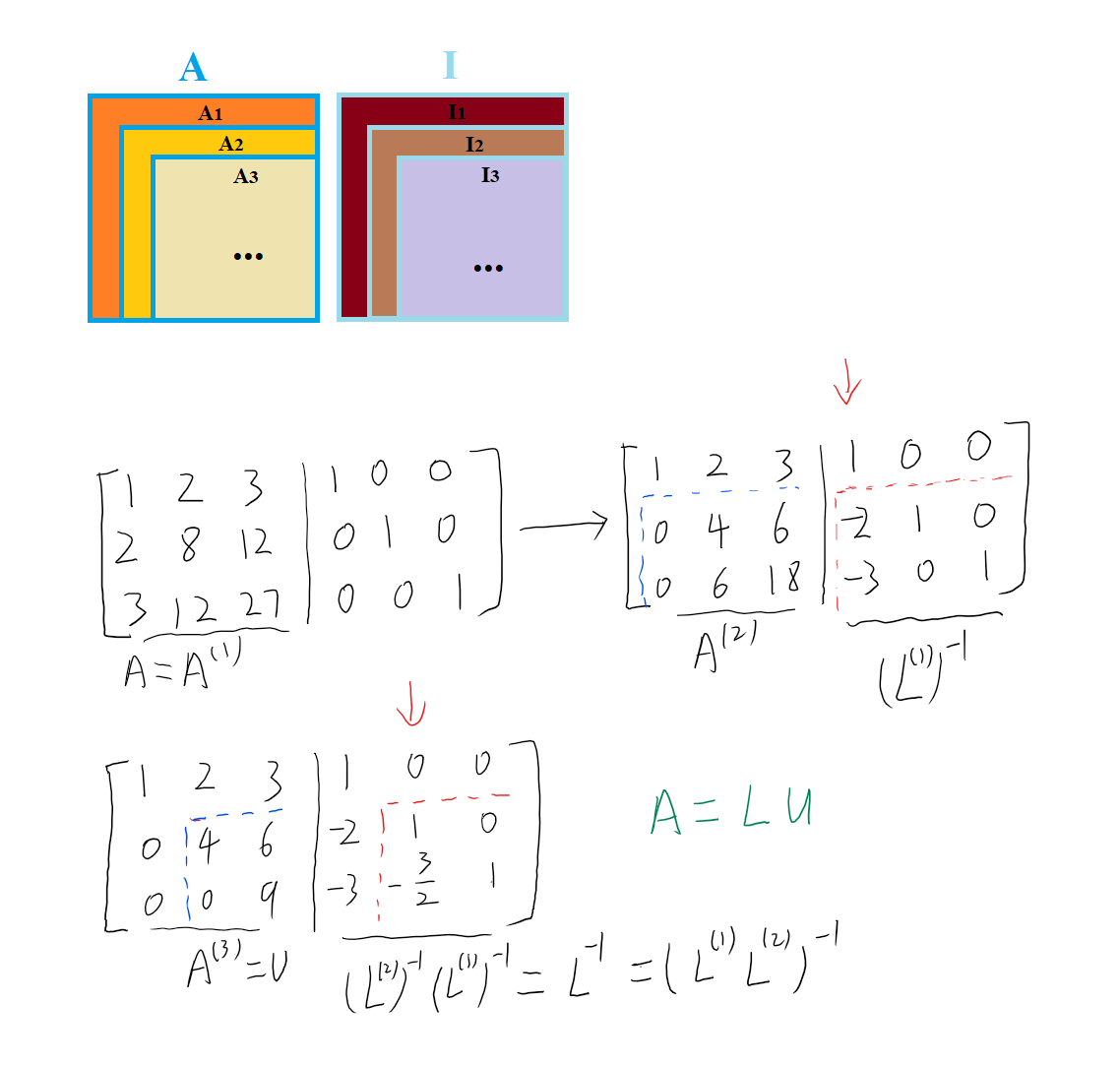
上述求解过程可通过如下方法简化:

将矩阵 \({\bm A}\) 与单位矩阵 \({\bm I}\) 组成新矩阵 \([{\bm A}|{\bm I}]\)
采用高斯消元法, 每次仅对待消元的子矩阵进行初等行变换, 如第二次消元时, 不再对第一列的元素进行初等变换
如此循环往复, 将矩阵 \({\bm A}\) 的主对角元素下的元素全部化为0, 矩阵 \({\bm A}\) 化为上三角矩阵 \({\bm U}\) , 矩阵 \({\bm I}\) 变为单位下三角矩阵的逆 \(({\bm L}^{(n-1)}\cdots {\bm L}^{(2)}{\bm L}^{(1)})^{-1} = {\bm L}^{-1}\) .

图 4.1 LU分解高斯消元简化¶

LU分解高斯消元简化, 三阶矩阵为例.

变元求解法¶

根据所求矩阵阶数, 设 \({\bm L}\) 为单位下三角矩阵, \({\bm U}\) 为上三角矩阵, 求解方程组 \({\bm A} = {\bm{LU}}\) 即可. 对于四阶矩阵, 求解方法如图 4.2 所示.

图 4.2 LU分解变元求解法¶

LU分解变元求解法, 四阶矩阵为例.

代码实现¶

在 Matlab 中可以通过函数 lu 求解.

上述例子的 matlab 代码求解如下:

>> A = [0 2 2;2 1 2; 0 2 1]
>> [L,U] = lu(A)

L =

     0     1     0
     1     0     0
     0     1     1


U =

     2     1     2
     0     2     2
     0     0    -1
>> [L,U, P] = lu(A)

   L =

        1     0     0
        0     1     0
        0     1     1


   U =

        2     1     2
        0     2     2
        0     0    -1


   P =

        0     1     0
        1     0     0
        0     0     1

4.2.5. 其它三角分解¶

根据上述介绍, 对 \({\bm {LDU}}\) 分解的形式进行一下组合和限定, 可以得到 Doolittle 分解, Crout 分解, 和 Cholesky 分解.

Crout 分解¶

设矩阵 \({\bm A}\) 有唯一的 \({\bm {LDU}}\) 分解, 将 \({\bm{LD}}\) 结合起来, 并用 \(\hat{{\bm L}}\) 表示, 则称

\[{\bm A} = {(\bm {LD}){\bm U}} = \hat{{\bm L}}{\bm U} \]

为矩阵 \({\bm A}\) 的 Crout 分解 . 可知 Crout 分解中, \({\bm U}\) 为单位上三角矩阵.

求解方法¶

上述变元求解法与高斯消元法即可求解.

Doolittle 分解¶

设矩阵 \({\bm A}\) 有唯一的 \({\bm {LDU}}\) 分解, 将 \({\bm{LD}}\) 结合起来, 并用 \(\hat{{\bm L}}\) 表示, 则称

\[{\bm A} = {{\bm L}(\bm {DU})} = {\bm L} \hat{{\bm U}} \]

为矩阵 \({\bm A}\) 的 Doolittle 分解 . 可知 Doolittle 分解中, \({\bm L}\) 为单位下三角矩阵.

求解方法¶

上述变元求解法与高斯消元法即可求解.

Cholesky 分解¶

设矩阵 \({\bm A}\) 为实对称正定矩阵, 有唯一的 \({\bm {LDU}}\) 分解, 将 \({\bm L}\) 与 \({\bm D}\) 的平方根结合起来, 记为 \({\bm G}\) 为下三角矩阵, 则称

\[{\bm A} = {{\bm G}{\bm G}^T} \]

为矩阵 \({\bm A}\) 的 Cholesky 分解 ( 或 平方根分解 , 对称三角分解 ).

易知, \({\bm G} = {\bm{L}\bar{\bm D}}\) 为下三角矩阵, 其中 \({\bm D} = {\rm diag}(d_1, d_2, \cdots, d_n)\) , \(\bar{{\bm D}} = {\rm diag}(\sqrt{d_1}, \sqrt{d_2}, \cdots, \sqrt{d_n})\) \(d_i>0\) .

提示

设矩阵 \({\bm A}\) 为实对称正定矩阵, 则有 \(\Delta_k > 0\) , 于是 \({\bm A}\) 有唯一的 \({\bm {LDU}}\) 分解, 其中, \({\bm D} = {\rm diag}(d_1, d_2, \cdots, d_n)\) , 记 \(\bar{{\bm D}} = {\rm diag}(\sqrt{d_1}, \sqrt{d_2}, \cdots, \sqrt{d_n})\) ,则有

\[{\bm A} = {\bm{L} {\bm D} {\bm U}} = {\bm{L} \bar{{\bm D}}^2 {\bm U}} \]

由 \({\bm A}^T = {\bm A}\) 知

\[{\bm U}^T {\bm D} {\bm L}^T = {\bm{L} {\bm D} {\bm U}} \]

由分解的唯一性知 \({\bm L} = {\bm U}^T\) , \({\bm U} = {\bm L}^T\)

所以有

\[{\bm A} = {\bm{L} {\bm D} {\bm U}} = {\bm{L} {\bm D} {\bm L}^T} \]

进一步地, 有

\[{\bm A} = {\bm{L} {\bm D} {\bm L}^T} = {\bm{L} \bar{{\bm D}} \bar{{\bm D}} {\bm L}^T} = {{\bm G}{\bm G}^T} \]

其中, \({\bm G} = {\bm{L}\bar{\bm D}}\) .

求解方法¶

上述变元求解法与高斯消元法即可求解,

可以先求 Doolittle 分解;
Doolittle 分解中的 \({\bm L}\) 即为 Cholesky 分解中的 \({\bm L}\) ;
Doolittle 分解中的 \(\hat{\bm U}\) 对角线元素构成 \({\bm D}\) ;
取 \({\bm L}\) 与 \({\bm D}\) 的平方根的乘积 \({\bm G} = {\bm L}\bar{\bm D}\) 即为所求.

注解

举个例子, 求以下矩阵的 Cholesky 分解

\[\left[ {\begin{array}{ccc} 5&2&{ - 4}\\ 2&1&2\\ { - 4}&{ - 2}&5 \end{array}} \right]. \]

解: 先求矩阵的 Doolittle 分解, 设 \({\bm L}\) 和 \(\hat{{\bm U}}\) 如下

\[\left[ {\begin{array}{ccc} 5&2&{ - 4}\\ 2&1&2\\ { - 4}&{ - 2}&5 \end{array}} \right] = \left[ {\begin{array}{ccc} 1&{}&{}\\ {{l_{21}}}&1&{}\\ {{l_{31}}}&{{l_{32}}}&1 \end{array}} \right]\left[ {\begin{array}{ccc} {{u_{11}}}&{{u_{12}}}&{{u_{13}}}\\ {}&{{u_{22}}}&{{u_{23}}}\\ {}&{}&{{u_{33}}} \end{array}} \right] \]

求解得到 \(l_{21}=\frac{2}{5}, l_{31}=-\frac{4}{5}, l_{32}=-2\) , \(u_{11}=5, u_{12}=2, u_{13}=-4\) , \(u_{22}=\frac{1}{5}, u_{23}=-\frac{2}{5}, u_{33}=1\) , 则有

\[{\bm{L}} = \left[ {\begin{array}{ccc} 1&{}&{}\\ {\frac{2}{5}}&1&{}\\ {\frac{{ - 4}}{5}}&{ - 2}&1 \end{array}} \right],\;{\bm{\hat U}} = \left[ {\begin{array}{ccc} 5&2&{ - 4}\\ {}&{\frac{1}{5}}&{\frac{{ - 2}}{5}}\\ {}&{}&1 \end{array}} \right] \]

易知 \({\bm D} = {\rm diag}(5, 1/5, 1)\) , \(\bar{\bm D} = {\rm diag}(\sqrt 5, 1/{\sqrt 5}, 1)\) , 从而有

\[{\bm G} = {\bm L}\bar{\bm D} = \left[ {\begin{array}{ccc} 1&{}&{}\\ {\frac{2}{5}}&1&{}\\ {\frac{{ - 4}}{5}}&{ - 2}&1 \end{array}} \right]\left[ {\begin{array}{ccc} {\sqrt 5 }&{}&{}\\ {}&{\frac{1}{{\sqrt 5 }}}&{}\\ {}&{}&1 \end{array}} \right] = \left[ {\begin{array}{ccc} {\sqrt 5 }&0&0\\ {\frac{{2\sqrt 5 }}{5}}&{\frac{1}{{\sqrt 5 }}}&{}\\ {\frac{{ - 4\sqrt 5 }}{5}}&{\frac{{ - 2\sqrt 5 }}{5}}&1 \end{array}} \right] \]

代码实现¶

在 Matlab 中可以通过函数 chol 求解.

>> A = [5 2 -4; 2 1 -2; -4 -2 5]

A =

  5     2    -4
  2     1    -2
 -4    -2     5

>> G = chol(A, 'lower')

G =

    2.2361         0         0
    0.8944    0.4472         0
   -1.7889   -0.8944    1.0000

>> G*G'

ans =

    5.0000    2.0000   -4.0000
    2.0000    1.0000   -2.0000
   -4.0000   -2.0000    5.0000