4.5. 奇异值分解¶
4.5.1. 概念¶
矩阵的奇异值¶
设 \({\bm A}\in{\mathbb C}_r^{m\times n} (r>0)\) , \({\bm A}^H{\bm A}\) 的特征值为
则称 \(\sigma_i = \sqrt{\lambda_i}, (i=1, 2, \cdots, n)\) 为 \({\bm A}\) 的 奇异值 (Singular Value); 当矩阵 \({\bm A}\) 为零矩阵时, 奇异值全为零.
\({\bm A}\) 的奇异值的个数等于 \({\bm A}\) 的列数;
\({\bm A}\) 的非零奇异值的个数等于 \({\bm A}\) 的秩;
设 \({\bm A}\in{\mathbb C}_r^{m\times n} (r>0)\) , 则存在 \(m\) 阶酉矩阵 \({\bm U}\) 和 \(n\) 阶酉矩阵 \({\bm V}\) , 使得
其中, \({\bm \Sigma} = {\rm diag}(\sigma_1, \sigma_2, \cdots, \sigma_r)\) , \(\sigma_i (i=1, 2, \cdots, r)\) 为矩阵 \({\bm A}\) 的全部非零特征值.
奇异值分解¶
奇异值分解 ( Singular Value Decomposition ) 是把一个矩阵 \({\bm A}_{m \times n}\) 分解为一个酉矩阵 ( unitary matrix) \({\bm U}_{m\times m}\) , 矩形对角矩阵 \({\bm S}_{m\times n}\) 与一个酉矩阵 \({\bm V}_{n\times n}\) 共轭转置乘积的分解.
称满足如下形式的矩阵分解为 奇异值分解 :
其中, \({\bm S}_{m\times n} = \left[ {\begin{array}{lll} {\bm{\Sigma }}_{r\times r}&{\bm{O}}_{r\times (n-r)}\\ {\bm{O}}_{(m-r)\times r}&{\bm{O}}_{(m-r)\times(n-r)} \end{array}} \right]\) .
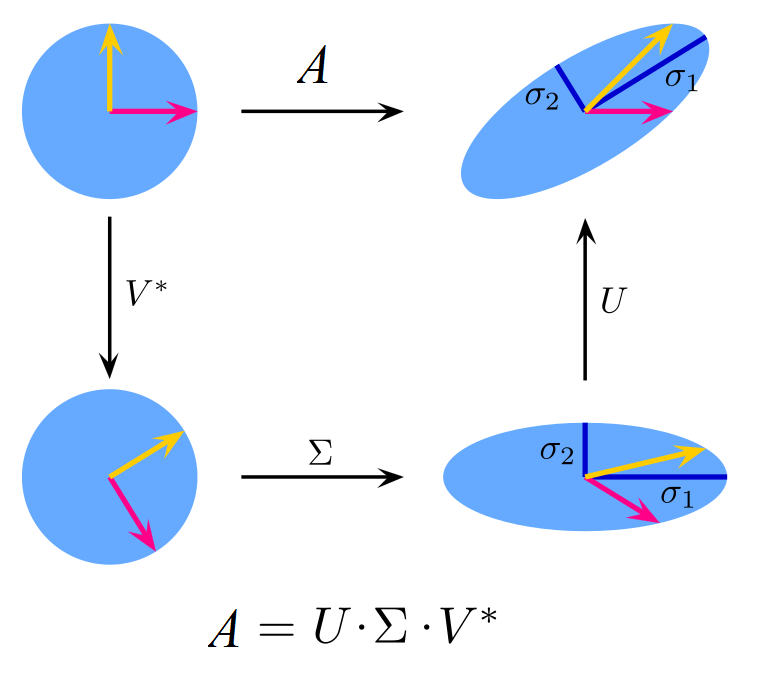
图 4.3 所示为奇异值分解示意图.
提示
矩阵 \({\bm A}\) 的奇异值由 \({\bm A}\) 唯一确定;
矩阵 \({\bm A}\) 的奇异值分解不唯一, 因为 \({\bm U, V}\) 一般不唯一;
矩阵 \({\bm U}\) 是 \({\bm A}{\bm A}^H\) 的特征向量
矩阵 \({\bm V}\) 是 \({\bm A}^H{\bm A}\) 的特征向量
注解
奇异值分解证明
4.5.2. 求解方法¶
设有矩阵 \({\bm A}\in{\mathbb C}_r^{m\times n} (r>0)\) , 求其奇异值分解的步骤如下:
计算矩阵 \({\bm A}^H{\bm A}\) 及其特征值和特征向量, 秩 \(r\) ;
根据特征值 \(\lambda_i\) , 求奇异值 \(\sigma_i\) , 并写出矩阵 \({\bm \Sigma}_{r}\times{r}\) 及矩形对角阵 \({\bm S}_{m \times n}\) ;
根据特征向量, 标准化特征向量并将特征向量按列依奇异值顺序排成矩阵 \({\bm V}\) , 取前 \(r\) 列构成 \({\bm V}_1\) ;
根据 \({\bm U}_1 = {\bm A}{\bm V}_1{\bm{\Sigma}}^{-1}\) 计算 \({\bm U}_1\) ;
取与 \({\bm U}_1\) 正交的矩阵 \({\bm U}_2\) , 合并得到 \({\bm U} = [{\bm U}_1 | {\bm U}_2]\) ;
最终求得矩阵 \({\bm A}\) 的奇异值分解 \({\bm A} = {\bm U} {\bm S} {\bm V}^H\) .
实例¶
求如下矩阵的 SVD分解
解: 由题意有
求得 \({{\bm{A}}^H}{\bm{A}}\) 特征值与特征向量分别为 \(\lambda_1 = 9, \lambda_2 = 1\) , 对应特征向量 \({\bm x}_1 = (1, -1)^T\) , \({\bm x}_2 = (1, 1)^T\)
从而有奇异值 \(\sigma_1 = 3, \sigma_2 = 1\) , 于是有
\[{\bm{\Sigma }} = \left[ {\begin{array}{ccc} {{\sigma _1}}&{}\\ {}&{{\sigma _2}} \end{array}} \right],\;\;{\bm{S}} = \left[ {\begin{array}{ccc} {{\sigma _1}}&0\\ 0&{{\sigma _2}}\\ 0&0 \end{array}} \right] = \left[ {\begin{array}{ccc} 3&0\\ 0&1\\ 0&0 \end{array}} \right] \]根据特征向量, 标准化特征向量并将特征向量按列依奇异值顺序排成矩阵, 由于秩 \(r = 2\) , 所以
\[{\bm V}_1 = {\bm V} = \left[ {\begin{array}{ccc} {\frac{1}{{\sqrt 2 }}}&{\frac{1}{{\sqrt 2 }}}\\ {\frac{1}{{\sqrt 2 }}}&{\frac{{ - 1}}{{\sqrt 2 }}} \end{array}} \right] \]根据 \({\bm U}_1 = {\bm A}{\bm V}_1{\bm{\Sigma}}^{-1}\) 计算 \({\bm U}_1\)
\[{\bm U}_1 = {\bm A}{\bm V}{\bm{\Sigma}}^{-1} = \left[ {\begin{array}{ccc} { - 1}&0\\ 0&1\\ 2&2 \end{array}} \right]\left[ {\begin{array}{ccc} {\frac{1}{{\sqrt 2 }}}&{\frac{1}{{\sqrt 2 }}}\\ {\frac{1}{{\sqrt 2 }}}&{\frac{{ - 1}}{{\sqrt 2 }}} \end{array}} \right]{\left[ {\begin{array}{ccc} 3&0\\ 0&1 \end{array}} \right]^{ - 1}} = \left[ {\begin{array}{ccc} {\frac{{ - 1}}{{3\sqrt 2 }}}&{\frac{{ - 1}}{{\sqrt 2 }}}\\ {\frac{1}{{3\sqrt 2 }}}&{\frac{{ - 1}}{{\sqrt 2 }}}\\ {\frac{4}{{3\sqrt 2 }}}&0 \end{array}} \right] \]取与 \({\bm U}_1\) 正交的矩阵 \({\bm U}_2\) , 合并得到 \({\bm U} = [{\bm U}_1 | {\bm U}_2]\)
\[{{\bm{U}}_2} = \left[ {\begin{array}{ccc} {\frac{2}{3}}\\ {\frac{{ - 2}}{3}}\\ {\frac{1}{3}} \end{array}} \right],\;{\bm{U}} = \left[ {\begin{array}{ccc} {\frac{{ - 1}}{{3\sqrt 2 }}}&{\frac{{ - 1}}{{\sqrt 2 }}}&{\frac{2}{3}}\\ {\frac{1}{{3\sqrt 2 }}}&{\frac{{ - 1}}{{\sqrt 2 }}}&{\frac{{ - 2}}{3}}\\ {\frac{4}{{3\sqrt 2 }}}&0&{\frac{1}{3}} \end{array}} \right] \]最终求得矩阵 \({\bm A}\) 的奇异值分解 \({\bm A} = {\bm U} {\bm S} {\bm V}^H\) .
代码实现¶
matlab代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 | >> A=[-1 0;0 1;2 2]
A =
-1 0
0 1
2 2
>> [U, S, V]=svd(A)
U =
-0.2357 -0.7071 0.6667
0.2357 -0.7071 -0.6667
0.9428 -0.0000 0.3333
S =
3.0000 0
0 1.0000
0 0
V =
0.7071 0.7071
0.7071 -0.7071
|
例子2
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 | >> A=[1 0 1;0 1 1; 0 0 0]
A =
1 0 1
0 1 1
0 0 0
>> [U, S, V]=svd(A)
U =
0.7071 -0.7071 0
0.7071 0.7071 0
0 0 1.0000
S =
1.7321 0 0
0 1.0000 0
0 0 0
V =
0.4082 -0.7071 0.5774
0.4082 0.7071 0.5774
0.8165 0.0000 -0.5774
>> U*S*V
ans =
0.2113 -1.3660 0.2989
0.7887 -0.3660 1.1154
0 0 0
>> U*S*V'
ans =
1.0000 -0.0000 1.0000
0.0000 1.0000 1.0000
0 0 0
|