6.1. 投影矩阵¶

6.1.1. 投影算子与投影矩阵¶

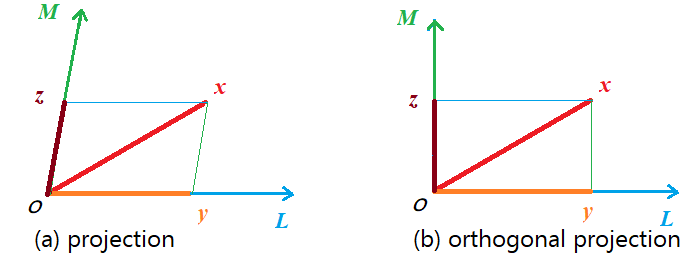
什么是投影¶

Definition 6.1 (投影)

设 \(\mathbb L\) 和 \(\mathbb M\) 均为 \({\mathbb C}^n\) 的子空间, 且 \(\mathbb L \oplus \mathbb M = {\mathbb C}^n\) , \(\forall {\bm x} \in {\mathbb C}^n\) 可分解为

\[{\bm x} = {\bm y} + {\bm z} , {\bm y}\in \mathbb L , {\bm z} \in \mathbb M \]

称 \({\bm y}\) 是 \({\bm x}\) 沿着 \(\mathbb M\) 到 \(\mathbb L\) 的投影 .

图 6.1 二维空间中的投影示意¶

二维空间中的投影示意

投影算子与投影矩阵¶

Definition 6.2 (投影算子与投影矩阵)

将 \(\forall {\bm x} \in {\mathbb C}^n\) 沿着 \(\mathbb M\) 到 \(\mathbb L\) 的投影变换称为沿着 \(\mathbb M\) 到 \(\mathbb L\) 的 投影算子 , 记为 \(P_{\mathbb L, \mathbb M}\) , 即

\[P_{\mathbb L, \mathbb M}{\bm x} = {\bm y}. \]

投影算子 \(P_{\mathbb L, \mathbb M}\) 在 \({\mathbb C}^n\) 中的基 \({\bm e}_1, {\bm e}_2, \cdots, {\bm e}_n\) 下的矩阵称为 投影矩阵 .

线性投影算子¶

Definition 6.3 (线性投影算子)

若对于 \(\forall {\bm x}_1, {\bm x}_2 \in {\mathbb C}^n\) 和 \(\lambda, \mu \in {\mathbb C}\) , 恒有

\[P_{\mathbb L, \mathbb M}(\lambda {\bm x}_1 + \mu {\bm x}_2) = \lambda P_{\mathbb L, \mathbb M}{\bm x}_1 + \mu P_{\mathbb L, \mathbb M}{\bm x}_2 \]

则称 \(P_{L,M}\) 为 线性算子 .

正交投影算子与正交投影矩阵¶

Definition 6.4 (正交投影算子与正交投影矩阵)

设 \(L\) 是 \({\mathbb C}^n\) 的子空间, 称沿着 \({\mathbb L}^{\perp}\) 到 \(\mathbb L\) 的投影算子 \(P_{\mathbb L, \mathbb L^{\perp}}\) 为 正交投影算子 , 简记为 \(P_{\mathbb L}\) .

正交投影算子 \(P_{\mathbb L, \mathbb L^{\perp}}\) 在 \({\mathbb C}^n\) 中的基 \({\bm e}_1, {\bm e}_2, \cdots, {\bm e}_n\) 下的矩阵称为 正交投影矩阵 .

性质¶

矩阵 \({\bm P}\) 为投影矩阵 \(\leftrightarrow\) \({\bm P}\) 为幂等矩阵.
矩阵 \({\bm P}\) 为正交投影矩阵 \(\leftrightarrow\) \({\bm P}\) 为幂等Hermite矩阵.

提示

若 \({\bm P}^2 = {\bm P}{\bm P} = {\bm P}\) , 则称 \({\bm P}\) 为 幂等矩阵 .