5.1. 特征值估计

5.1.1. 特征值的界

定理1: 设 \({\bm A} = (a_{ij})_{n\times n} \in {\mathbb R}^{n\times n}\) , 令 \(M = \mathop {{\rm{max}}}\limits_{1 \le i,j \le n} \frac{1}{2}|{a_{ij}} - {a_{ji}}|\) , 若 \(\lambda\) 表示 \({\bm A}\) 的任一特征值, 则 \(\lambda\) 的虚部 \({\rm Im}(\lambda)\) 满足不等式

\[|{Im(\lambda)}| \leq M\sqrt{\frac{n(n-1)}{2}}. \]

定理2: 设 \({\bm A}\in {\mathbb C}^{n\times n}\) , 则 \({\bm A}\) 的任一特征值 \(\lambda\) 满足

\[|\lambda| \leq \|{\bm A}\|_{m_{\infty}}, \\ |{\rm Re}(\lambda)| \leq \frac{1}{2}\|{\bm A} + {\bm A}^H\|_{m_{\infty}}, \\ |{\rm Im}(\lambda)| \leq \frac{1}{2}\|{\bm A} - {\bm A}^H\|_{m_{\infty}} . \]

定理3: 设 \({\bm A} = (a_{ij})_{n\times n} \in {\mathbb C}^{n\times n}\) 的特征值为 \(\lambda_1, \lambda_2, \cdots, \lambda_n\) , 则

\[\sum_{i=1}^n{ |\lambda_i|^2 \leq \sum_{i,j=1}^n{|a_{ij}|^2} = \|{\bm A}\|_F^2 } , \]

当且仅当 \({\bm A}^H {\bm A} = {\bm A}{\bm A}^H\) 时, 等号成立.

5.1.2. 特征值的包含区域

盖尔圆

什么是盖尔圆

Definition 5.1 (盖尔圆(一般教材定义))

设 \({\bm A} = (a_{ij})_{n\times n} \in {\mathbb C}^{n\times n}\) , 称不等式

\[|z - a_{ii}| \leq R_i , R_i = R_i({\bm A}) = \sum_{j=1,j\neq i}^n |a_{ij}| \]

在复平面上所确定的区域为矩阵 \({\bm A}\) 的第 \(i\) 个 盖尔圆 (Gerschgorin) , 记为 \(G_i\) , \({\bm R}_i\) 为不包括 \(a_{ii}\) 的行和, 称为盖尔圆 \(G_i\) , \((i = 1, 2, \cdots, n)\) 的半径.

Definition 5.2 (盖尔圆(我的定义))

实际上, 在上述定义中, 若令半径为

\[|z - {a_{ii}}| \le {R_i},{R_i} = {R_i}({\bm{A}}) = \min \left( {\sum\limits_{j = 1,j \ne i}^n | {a_{ij}}|{\rm{,}}\;\sum\limits_{i = 1,i \ne j}^n | {a_{ij}}|} \right) \]

显然确定特征值范围会变得更为简单, 不知道为什么不这样定义.

注解

半径 \(R_i\) 也可以按列求和得到, 这是因为 \({\bm A}\) 与 \({\bm A}^T\) 的特征值相同.

定理与结论

  • 盖尔圆定理1: 矩阵 \({\bm A} = (a_{ij})_{n\times n} \in {\mathbb C}^{n\times n}\) 的一切特征值都在它的 \(n\) 个盖尔圆的并集内.

  • 盖尔圆定理2: 矩阵 \({\bm A} = (a_{ij})_{n\times n} \in {\mathbb C}^{n\times n}\) 的联通部分由几个盖尔圆组成, 该部分就包含几个特征值 (盖尔圆相重时重复计数, 特征值相同时重复计数).

注解

结论:

  • 若矩阵 \({\bm A}\) 的盖尔圆 \(G_i\) 关于实轴对称, 则特征值 \(\lambda_i\) 为实数.

  • 若矩阵 \({\bm A}\) 的盖尔圆 \(G_i\) 各自孤立不连通, 则 \({\bm A}\) 有 \(n\) 个互不相同的特征值.

特征值的隔离问题

设矩阵 \({\bm A} = (a_{ij})_{n\times n} \in {\mathbb C}^{n\times n}\) , 构造对角矩阵 \({\bm D} = {\rm diag}(d_1, d_2, \cdots, d_n)\) , 其中 \(d_i > 0, i = 1, 2, \cdots, n\) , 由于矩阵

\[{\bm B} = {\bm D}{\bm A}{\bm D}^{-1} = \left(\frac{d_i}{d_j}a_{ij}\right)_{n\times n} \]

相似于 \({\bm A}\) , 所以矩阵 \({\bm B}, {\bm A}\) 的特征值集合相同.

提示

  • 取 \(d_i < 1, d_k = 1, k \neq i\) , 可使第 \(i\) 个盖尔圆的半径减小

  • 取 \(d_i > 1, d_k = 1, k \neq i\) , 可使第 \(i\) 个盖尔圆的半径增大

举个例子

应用盖尔圆定理隔离如下矩阵的特征值

\[{\bm{A}} = \left[ {\begin{array}{ccc} {20}&3&1\\ 2&{10}&2\\ 8&1&0 \end{array}} \right] \]

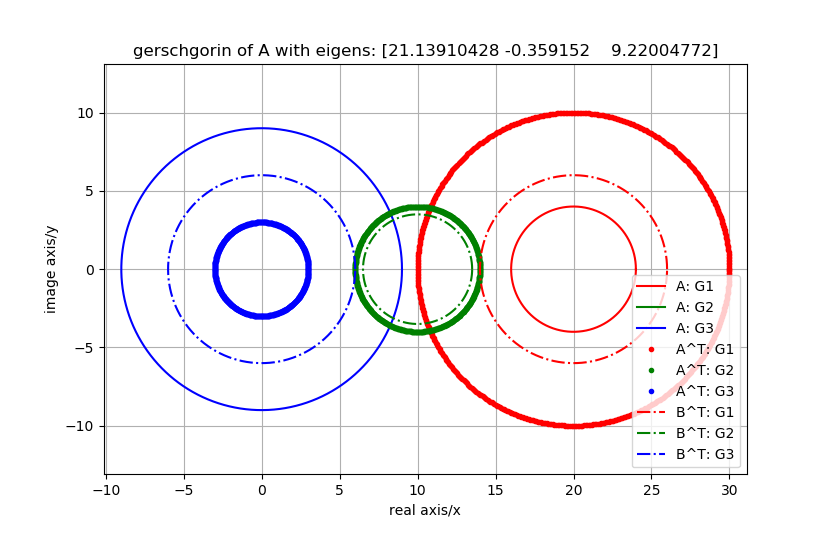
解: 矩阵 \({\bm A}\) 的三个盖尔圆为 \(G_1: |z-20| \leq 4\) , \(G_2: |z-10| \leq 4\) , \(G_3: |z-0| \leq 9\) , 如图所示

易知盖尔圆 \(G_2, G_3\) 相交, \(G_1\) 孤立, 构造矩阵 \(D = {\rm diag}(1, 1, 1/2)\) 使得 \(G_3\) 的半径减小, 则有

\[{\bm{B}}{\rm{ = }}{\bm{DA}}{{\bm{D}}^{ - 1}} = \left[ {\begin{array}{ccc} 1&{}&{}\\ {}&1&{}\\ {}&{}&{1/2} \end{array}} \right]\left[ {\begin{array}{ccc} {20}&3&1\\ 2&{10}&2\\ 8&1&0 \end{array}} \right]\left[ {\begin{array}{ccc} 1&{}&{}\\ {}&1&{}\\ {}&{}&2 \end{array}} \right] = \left[ {\begin{array}{ccc} {20}&3&1\\ 2&{10}&4\\ 4&{1/2}&0 \end{array}} \right] \]

矩阵 \({\bm B}^T\) 的三个盖尔圆为 \(G_1: |z-20| \leq 4\) , \(G_2: |z-10| \leq 4\) , \(G_3: |z-0| \leq 9\) , 如 fig-demo_Gerschgorin_exp1 所示, 它们相互孤立,

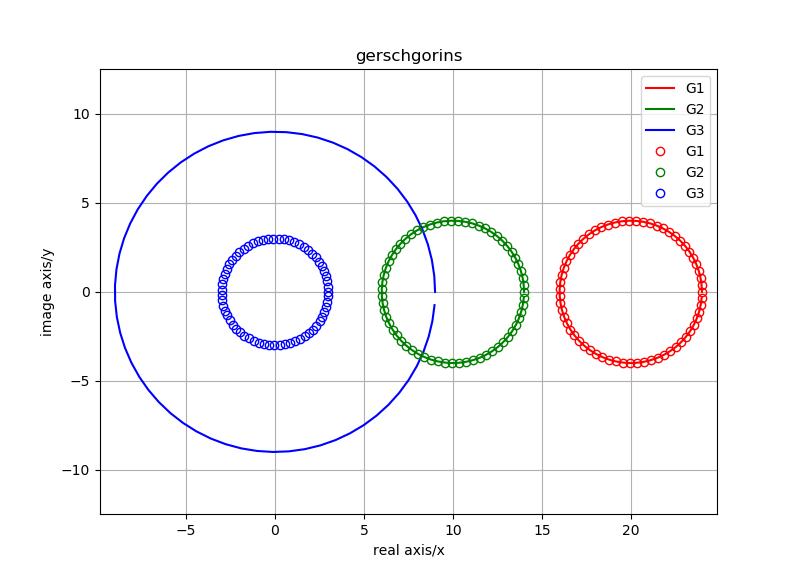
Gerschgorin

图 5.1 矩阵 \({\bm A}, {\bm A}^T, {\bm B}^T\) 的盖尔圆

矩阵 \({\bm A}, {\bm A}^T, {\bm B}^T\) 的盖尔圆示意图.

实际上若采用盖尔圆定义2, 可以很容易得到 fig-demo_Gerschgorin 所示结果

Gerschgorin

图 5.2 矩阵 \({\bm A}\) 的盖尔圆

矩阵 \({\bm A}\) 的盖尔圆示意图, 每个盖尔圆的半径取为元素所在行元素和, 与元素所在列元素和中最小的那个.

上述结果实验代码为

代码 5.1 demo_Gerschgorin.py
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
import numpy as np
import pytool

A = [[20, 3, 1], [2, 10, 2], [8, 1, 0]]

A = np.array(A)
D = np.diag((1, 1, 1 / 2))
B = np.dot(D, A)
B = np.dot(B, np.linalg.inv(D))

Cis = []
Ris = []
Cis1, Ris1 = pytool.gerschgorin(A)
Cis2, Ris2 = pytool.gerschgorin(A.transpose())
Cis3, Ris3 = pytool.gerschgorin(B.transpose())

Cis = Cis + Cis1
Ris = Ris + Ris1

Cis = Cis + Cis2
Ris = Ris + Ris2

Cis = Cis + Cis3
Ris = Ris + Ris3

colorlines = ['-r', '-g', '-b', '.r', '.g', '.b', '-.r', '-.g', '-.b']

evalues, evectors = np.linalg.eig(A)

Title = "gerschgorin of A with eigens: " + str(evalues)
Legend = ['A: G1', 'A: G2', 'A: G3', 'A^T: G1',
          'A^T: G2', 'A^T: G3', 'B^T: G1', 'B^T: G2', 'B^T: G3']

pytool.plot_circles(
    Cis=Cis, Ris=Ris, colorlines=colorlines, dTheta=0.01, title=Title, legend=Legend)

应用

  • 判定矩阵是否可逆: 矩阵的行列式的值等于矩阵特征值的乘积, 由于行列式不为零的矩阵可逆, 所以可逆矩阵的特征值不等于零, 借助盖尔圆判定特征值的取值