4.2. 距离多普勒成像¶
4.2.1. 距离多普勒方法¶
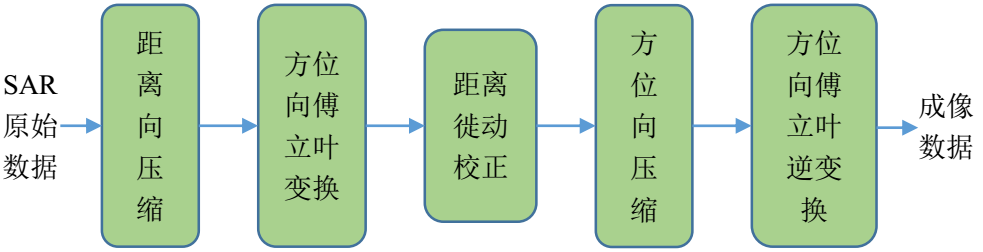
图 4.29 Framework of Range Doppler Algorithm¶
提示
对于大斜视SAR, 距离压缩中包含二次距离压缩 (Second Rage Compression, SRC), 距离徙动校正也不一样.
小斜视下的RDA¶
SAR原始数据¶
SAR 原始数据是指SAR系统接收到的数据, 数据先被解调至基带, 距离频率中心被置零, 解调后的基带信号为 (参见: Section-SARSignalSystemOverviewSARRadar 小结, 式.2.35 )
距离压缩¶
将SAR基带信号的距离维FFT变换 \(S_r(\eta, f_\tau)\) 与距离向匹配滤波器 \(H_r(f_{\tau})\) 相乘;
进行距离维逆FFT完成距离维压缩.
匹配滤波器的生成与实现方式不同, 距离压缩的方式也不同. 如采用复制脉冲尾部补零经FFT后的复共轭作为滤波器.
SAR回波信号 \(s(\eta, \tau)\) 的距离维傅里叶变换为
其中, \(G\) 为常数, \(W_r(f_\tau)=w_r(f_\tau/K_r)\) 是距离频谱的包络.
匹配滤波的目的在于消除上式中的第二个指数项, 故取距离向匹配滤波器为
对滤波器输出进行距离向IFFT, 得到距离向压缩输出为
其中, 压缩脉冲包络 \(p_r(\tau)\) 为窗函数 \(W_r(f_{\tau})\) 的傅里叶逆变换: 对于矩形窗, \(p_r(\tau)\) 为 \(\rm sinc\) 函数, 对于锐化窗(kasier), \(p_r(\tau)\) 为旁瓣较低的 \(\rm sinc\) 函数. \(G\) 为包括散射系数在内的总增益, 常假定为1.
方位向傅里叶变换¶
小斜视下, 波束指向接近零多普勒方向, 且 \(R_0 \gg V_r\eta\) , 可将距离近似为抛物线
代入距离向压缩输出表达 式.4.3 得
方位向的时频关系为 \(f_{\eta} = -K_a\eta\) , 其中记方位向调频率 \(K_a \thickapprox \frac{2V_r^2}{\lambda R_0}\) , 代入上式, 方位向FFT后的信号变为
其中, \(W_a(f_{\eta} - f_{\eta_c})\) 为方位向天线方向图 \(w_a(\eta-\eta_c)\) 的频域形式. 第一个指数项含有目标固有的相位信息(干涉极化)与图像强度无关. 第二项指数项为具有线性调频特性的频域方位调制. 距离徙动补偿项为
距离徙动校正¶
距离徙动校正 (RCMC) 有两种实现方式.
一种是在距离多普勒域进行距离插值, 可以基于 \(\rm sinc\) 函数进行插值处理. 需要校正的 RCM 为方位频率 \(f_\eta\) 的函数, 也是 \(R_0\) 的函数:
距离徙动校正因子:
另一种是基于RCM在有限区域内不随距离改变, 从而可以通过 FFT --> 线性相位相乘 --> IFFT 实现, 相位乘法器为
但这种需要对数据进行分块, 复杂度高, 一般不采用.
基于 \(\rm sinc\) 插值进行RCMC后的信号变为
有关实验请参考 距离徙动校正 小节.
方位压缩¶
将方位向FFT后的 \(S_a(f_{\eta}, \tau)\) (或RCMC后的 \(S_{rcmc}(f_{\eta}, \tau)\) ) 与方位向匹配滤波器 \(H_a(f_{\eta})\) 相乘;
进行方位维逆FFT完成方位维压缩.
方位向压缩在于消除方位向FFT(或RCMC)后的信号的第二个指数项成分, 因而匹配滤波器为其复共轭:
实现方式如下
匹配滤波后的输出变为
经过方位向IFFT后的压缩信号为
其中, \(p_a\) 为方位向冲击响应的幅度, 与 \(p_r\) 一样为 \({\rm sinc}\) 函数. 至此, 目标已经被校正到 \(\eta = 0, \tau=2R_0/c\) 处.
提示
在非零斜视角下, 使用抛物线近似距离使得相位精度不能被保证, 可以使用双曲相位形式的匹配滤波器, 即不进行近似.
多视处理¶
多视处理可以减少相干斑点噪声, 其主要思路是在方位向做平均滤波, 当然也可以在距离向上做滤波.
大斜视下的RDA¶
在低斜视时, 距离等式近似为时间的抛物线方程式, 抛物线模型相当于时域中的线性调频信号, 变换到频域后的信号也具有线性调频形式 [1]. 在大斜视角时, 距离等式应该采用更为精确的双曲线模型, 此时时频间呈非线性关系, 用于距离徙动补偿和方位匹配滤波器的距离应采用新的距离方程, 大斜视引入较强的距离和方位耦合(散焦), [1] 可以通过二次距离压缩来校正.
提示
下述中, 将徙动因子 \(D(f_\eta, V_r)\) 展开并忽略 \(f_\eta\) 二阶及以上项, 则退化为低斜视角下的表达式.
二次距离压缩¶
在含有交叉耦合的信号的距离多普勒域信号中的调频率由 \(K_r\) 变为了 \(K_m\) [1] p170. 其中,
二次压缩滤波器中的调频率为
首先使用调频率为 \(K_r\) 的滤波器进行匹配滤波实现初级压缩, 再使用调频率为 \(K_{src}\) 的滤波器进行次级的匹配滤波实现二次压缩, 因而叫二次距离压缩. 二次距离压缩的滤波器为
该滤波器与距离 \(R_0\) 和方位向频率 \(f_\eta\) 有关. 在距离频域中, SRC滤波器可以并入距离压缩滤波器中, 合并的滤波器为
提示
二次距离压缩的实现方式
二次距离压缩的实现方式有三种:
方式一: 在距离多普勒域中, 随RCMC插值一同进行
方式二: 通过二维频域中的相位相乘实现
方式三: 在距离频率 - 方位时域中进行
多普勒相位补偿¶
对于斜视SAR, 还需要做多普勒相位补偿 (Doppler Phase Compensation, DPC), 补偿滤波器为
其中, \(f_{\eta}\) 为方位向频率, \(Y_c\) 为场景中心在方位向坐标轴上的投影, \(V_s\) 为SAR平台速度.
4.2.2. 实验与分析¶
真实数据实验¶
实验数据¶
实验所采用数据为 RADARSAT1 卫星上的合成孔径雷达获取的温哥华地区的图像. 具体介绍参见 RADARSAT 产品介绍 小节.
实验说明¶
分析RDA算法中二次距离压缩与距离徙动补偿的影响.
实验代码¶
Python实现代码, 参见文件 demo_RADARSAT1.py .
实验结果¶
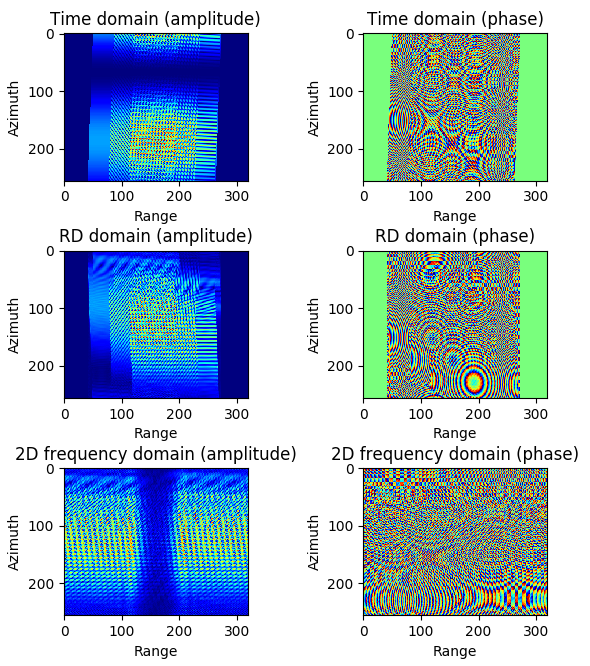
RADARSAT1 获取的史丹利公园的SAR数据幅度与相位
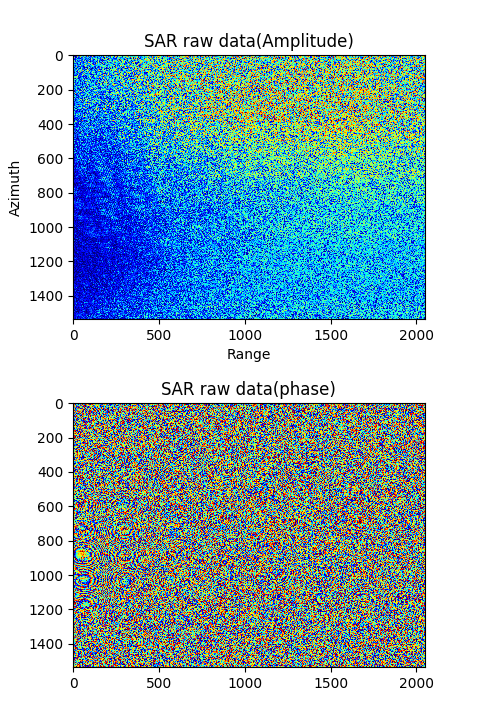
图 4.38 SAR raw data amplitude and phase of Stanley Park.¶
SAR raw data amplitude and phase of Stanley Park.
RDA 成像结果 (以下结果均含多普勒相位补偿操作)

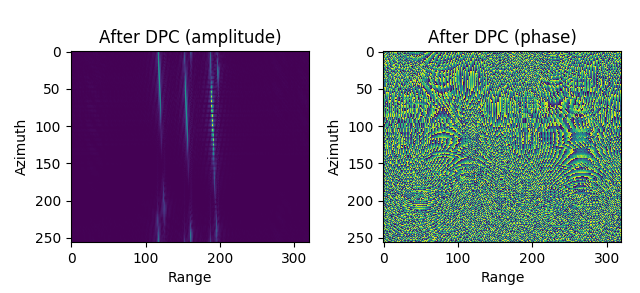
图 4.39 Imaging result of RDA (without SRC, without RCMC)¶
Imaging result of RDA (without SRC, without RCMC)

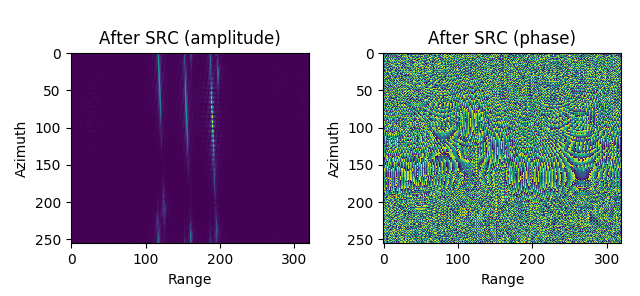
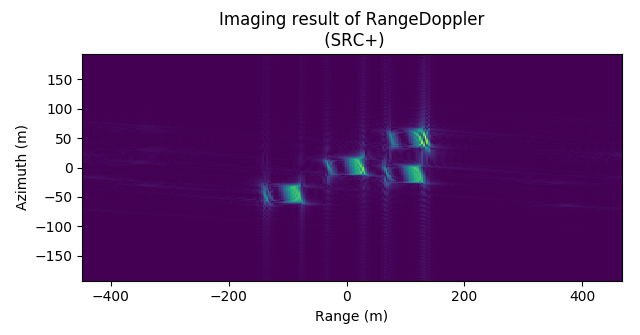
图 4.40 Imaging result of RDA (with SRC, without RCMC)¶
Imaging result of RDA (with SRC, without RCMC)

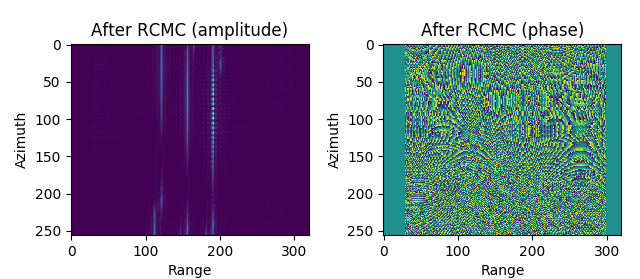
图 4.41 Imaging result of RDA (without SRC, with RCMC(sinc 32))¶
Imaging result of RDA (without SRC, with RCMC(sinc 32))

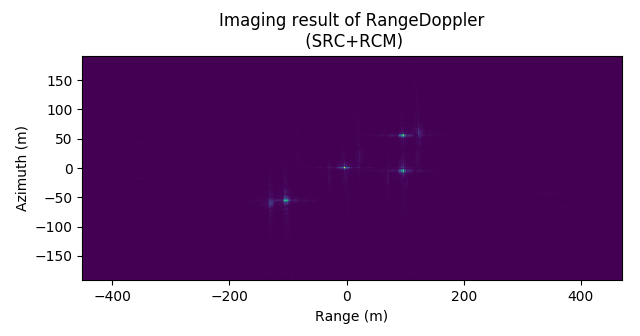
图 4.42 Imaging result of RDA (with SRC, with RCMC(sinc 32))¶
Imaging result of RDA (with SRC, with RCMC(sinc 32))