4.5. 压缩感知成像

4.5.1. 压缩感知SAR成像

越来越多的基于压缩感知的SAR成像方法被提出 [3][4][5] .

匹配追踪用于量子模拟 [1]

SAR imaging process can be formulated as

${\bm s} = {\bm A}{\bm g} + {\bm n},$

where, ${\bm s}$ is the $m = MN\times 1$ recieved SAR raw data vector in phase history domain, $\bm g$ is the $n = HW \times 1$ reflection vector of scene. $\bm A$ represents the the mapping from scene to SAR raw data. $\bm n$ is the noise vector.

If $\bm g$ is not sparse enough, assume that exist a basis ${\bm D} = ({\bm d}_1, {\bm d}_2, \cdots, {\bm d}_n)$ that satisfies ${\bm g} = {\bm D}{\bm x}$ , where, $\bm x$ is a $K$ sparse $n\times 1$ vector, and $\bm D$ is the so called dictionary matrix of size $n\times n$ .

Our goal is minimize

$\mathop {\rm min}\limits_{\bm x}\|{\bm x}\|_p, \ \ s.t. \ {\bm s} = {\bm A}{\bm D}{\bm x} + {\bm n},$

i.e.

$\mathop {\rm min}\limits_{\bm{x}} = \|{\bm s} - {\bm A}{\bm D}{\bm x}\|_2 + \lambda \|{\bm x}\|_p,$

where, $\lambda$ is the balance factor, and $|\cdot|_p, (0<p<1)$ is the $\ell_p$ norm.

Let ${\bm \Phi} = {\bm A}{\bm D}$ , then we have

$\mathop {\rm min}\limits_{\bm{x}} = \|{\bm s} - {\bm \Phi}{\bm x}\|_2 + \lambda \|{\bm x}\|_p.$

Note that, if ${\bm s, \Phi, x} \in {\mathbb C}$ , the problem changes to

${\mathop{\rm Re}\nolimits} ({\bm{s}}) + j{\rm Im}({\bm{s}}) = {\rm Re}({\bm \Phi}{\bm x}) + j{\mathop{\rm Im}\nolimits} ({\bm \Phi}{\bm x})$

so we have:

$\left[ {\begin{array}{ccc} {{\mathop{\rm Re}\nolimits} ({\bm{s}})}\\ {{\mathop{\rm Im}\nolimits} ({\bm{s}})} \end{array}} \right] = \left[ {\begin{array}{ccc} {{\mathop{\rm Re}\nolimits} ({\bm{\Phi }})}&{ - {\mathop{\rm Im}\nolimits} ({\bm{\Phi }})}\\ {{\rm Im}({\bm{\Phi }})}&{{\mathop{\rm Re}\nolimits} ({\bm{\Phi }})} \end{array}} \right]\left[ {\begin{array}{ccc} {{\mathop{\rm Re}\nolimits} ({\bm{x}})}\\ {{\mathop{\rm Im}\nolimits} ({\bm{x}})} \end{array}} \right]$

提示

对于非稀疏场景, 无需先对场景进行稀疏表示, 再进行观测; 然而在重构信号时, 由于信号非稀疏, 需要假设其在某一字典下稀疏.

ABC

4.5.2. 实验与分析

仿真数据

实验说明

• 仿真场景大小: $32 \times 32$

• 回波矩阵大小: $32 \times 32$

• 稀疏表示字典: 无, DCT , DWT

• 优化方法: Lasso , OMP

仿真点目标场景图及仿真生成点SAR原始数据幅度与相位图如下:

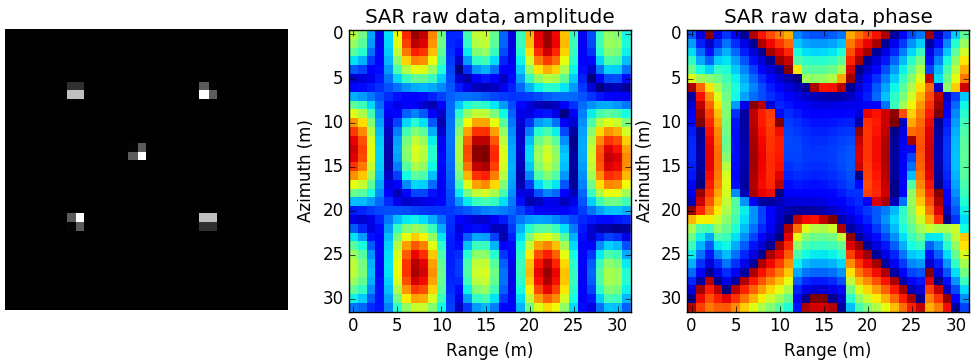
图 4.61 仿真点目标场景图, 仿真SAR原始数据幅度相位图

仿真船只场景图及仿真生成点SAR原始数据幅度与相位图如下:

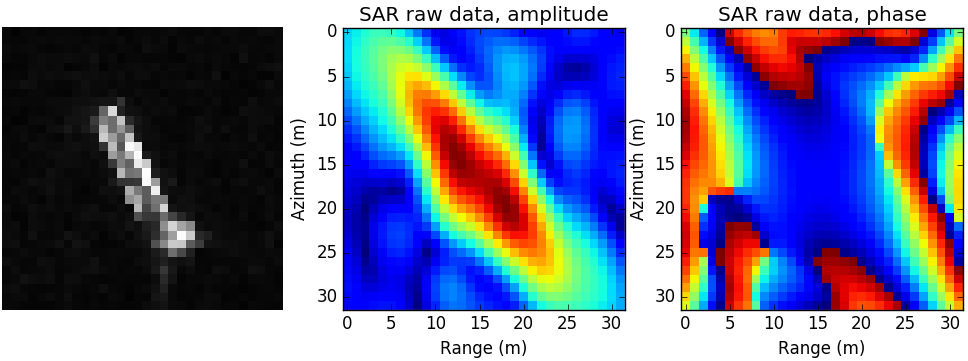
图 4.62 仿真船只场景图及仿真生成点SAR原始数据幅度与相位图如下

仿真荷花场景图及仿真生成点SAR原始数据幅度与相位图如下:

图 4.63 仿真荷花场景图及仿真生成点SAR原始数据幅度与相位图如下

实验代码

实验结果

1. OMP优化, 不采用字典进行稀疏表示, 和采用DCT字典进行稀疏表示的结果如下:

点目标结果

图 4.64 Compressive Sensing based and RDA Imaging Results of points.

船只结果:

图 4.65 Compressive Sensing based and RDA Imaging Results of ship.

荷花结果:

图 4.66 Compressive Sensing based and RDA Imaging Results of lotus.

2. Lasso优化, 不采用字典进行稀疏表示, 和采用DCT字典进行稀疏表示的结果如下:

点目标结果

图 4.67 Compressive Sensing based and RDA Imaging Results of points.

船只结果:

图 4.68 Compressive Sensing based and RDA Imaging Results of ship.

荷花结果:

图 4.69 Compressive Sensing based and RDA Imaging Results of lotus.

注解

由实验结果可知:

• 场景的稀疏性决定了重构的性能, 越稀疏重构越精确

• 字典的选择很重要

真实数据

实验说明

由于压缩感知方法占用内存空间大, 该数据为RADARSAT1一景数据中的一小块区域, 区域大小为 $128\times 128$ .

实验代码

实验结果