9.1. 基础分析实验

9.1.1. 实验说明

通过点目标仿真, 分析理解调频率, 分辨率等概念.

Python实现代码, 参见文件 demo_AirboneSAR_Points.py .

实验参数

实验参数如 表 9.1 所示, 类似文献 [1] 中138页的点目标仿真实验中的参数, 部分参数不一致.

表 9.1 仿真的机载SAR平台参数

参数

符号

数值

单位

平台高度

\(H\)

10

\(km\)

雷达有效速度

\(V\)

150

\(m/s\)

场景中心斜距

\(R_c\)

20

\(km\)

雷达载频

\(f_0\)

5.3

\(GHz\)

发射脉冲时宽

\(T_p\)

2.5

\(μs\)

距离向调频率

\(K_r\)

-20.0e12, +20.0e12

\(Hz/s\)

距离向采样率

\(F_{r}\)

60.0

\(MHz\)

距离向采样点数

\(N_{r}\)

320

方位向采样率

\(F_{a}\)

100

\(Hz\)

方位向采样点数

\(N_{a}\)

256

距离向天线孔径

\(L_{r}\)

12.0

\(m\)

方位向天线孔径

\(L_{a}\)

3.0

\(m\)

下视角

\(\theta_{d}\)

30

\(°\)

波束距离向宽度

\(\theta_{b}\)

1.32, 1.32, 1.32

\(°\)

波束斜视角

\(\theta_{s}\)

0.0, 3.5, 21.9

\(°\)

波束中心偏移时间

\(\eta_{c}\)

0.0, -8.1, -49.7

\(s\)

多普勒中心频率

\(f_{\eta_c}\)

0.0, 320, 1975

\(Hz\)

根据上表参数, 可以计算出如下参数

  • 场景中心斜距: \(R_c = H / {\rm sin}\theta_d ≈ 20000.0m\)

  • 最短斜距: \(R_0 = R_c {\rm cos} \theta_s ≈ 18556.7m\)

  • 斜距分辨率: \(\Delta_r = \frac{c}{2B_r} = \frac{c}{2|K_r|T_p} ≈ 2.99m\)

  • 地距分辨率: \(\Delta_x = \Delta_r /{\rm cos}\theta_i ≈ 3.46m\)

  • 方位向距离分辨率: \(\Delta_a=\Delta_y = L_a/2 = 1.5m\)

  • 场景中心坐标: \((x_c, y_c)\), \(x_c = {\sqrt{R_0^2 - H^2}}\), \(y_c = R_c{\rm sin}\theta_s\)

    • \(\theta_s = 0, x_c=17320.50m, y_c=0m\)

    • \(\theta_s = 3.5, x_c=17286.62m, y_c=1221.45m\)

    • \(\theta_s = 21.9, x_c=15640.55m, y_c=7462.73m\)

  • 近地点斜距: \(R_{near} = H/{\rm sin}(\theta_d+\theta_b/2)\)

    • \(\theta_s = 0, R_{near}=19609.59m\)

    • \(\theta_s = 3.5, R_{near}=19610.05m\)

    • \(\theta_s=21.9, R_{near}=19609.59m\)

  • 远地点斜距: \(R_{far} = H/{\rm sin}(\theta_d-\theta_b/2)\)

    • \(\theta_s = 0, R_{far}=20409.03m\)

    • \(\theta_s = 3.5, R_{far}=20409.03m\)

    • \(\theta_s=21.9, R_{far}=20409.03m\)

  • 刈幅宽度 (swath size): \(S_x = (H/{\rm tan}(\theta_d-\theta_b/2) - H/{\rm tan}(\theta_d+\theta_b/2)){\rm cos}\theta_s = 921.9{\rm cos}\theta_s\)

    • \(\theta_s = 0, S_x=923.05m\)

    • \(\theta_s = 3.5, S_x=921.91m\)

    • \(\theta_s = 21.9, S_x=880.48m\)

  • 方位向成像宽度: \(S_y = VT_{sa} = 384.0m\)

  • 成像区域: \((x_{min}, x_{max}, y_{min}, y_{max})\)

    • \(\theta_s = 0, SA=(-461.53, 461.53, -192.0, 192.0)\)

    • \(\theta_s = 3.5, SA=(-460.96, 460.95, -192.0, 192.0)\)

    • \(\theta_s = 21.9, SA=(-440.58, 439.91, -192.0, 192.0)\)

9.1.2. 调频方向分析

设置目标位于场景中心处, 即相对坐标 \((0, 0)\), 目标强度为 1, 观察不同调频方向, 不同斜视角下的时域(原始信号), 距离多普勒域(原始信号在方位维做FFT), 频域(原始信号在距离和方位上均做FFT)的幅度相位.

零斜视角, \(\theta_s=0.0^°\), 正调频

The property of point target in Range Doppler domain (positive frequency modulation).

图 9.1 The property of point target in different domain (positive frequency modulation).

零斜视角, \(\theta_s=0.0^°\), 负调频

The property of point target in Range Doppler domain (negative frequency modulation).

图 9.2 The property of point target in different domain (negative frequency modulation).

斜视角 \(\theta_s=3.5^°\) , 正调频

The property of point target in Range Doppler domain (positive frequency modulation).

图 9.3 The property of point target in different domain (positive frequency modulation).

斜视角 \(\theta_s=3.5^°\) , 负调频

The property of point target in Range Doppler domain (negative frequency modulation).

图 9.4 The property of point target in different domain (negative frequency modulation).

斜视角 \(\theta_s=21.9^°\) , 正调频

The property of point target in Range Doppler domain (positive frequency modulation).

图 9.5 The property of point target in different domain (positive frequency modulation).

斜视角 \(\theta_s=21.9^°\) , 负调频

The property of point target in Range Doppler domain (negative frequency modulation).

图 9.6 The property of point target in different domain (negative frequency modulation).

9.1.3. 分辨率分析

设置目标为 \((0.0, 0.0), (-6, -6), (-6, 6), (6, -6), (6, 6), (9, 9)\), 目标强度均为1, 进行如下设置.

  • 方位向设置

    • 采样率: \(F_{sa} = 100Hz\) 和 \(F_{sa} = 200Hz\)

    • 采样点: \(N_{sa} = 256\) 和 \(N_{sa} = 1024\)

    • 天线孔径: \(L_{a} = 6.0m\), \(L_{a} = 3.0m\) 和 \(L_{a} = 1.5m\)

  • 距离向设置

    • 采样率: \(F_{sr} = 60.0e6Hz\)

    • 采样点: \(N_{sr} = 320\) 和 \(N_{sr} = 1280\)

    • 调频率: \(K_{r} = -20.0e12Hz/s\)

    • 脉宽: \(Tp = 2.5e-6s\) 和 \(Tp = 5.0e-6s\)

方位向的分辨率由方位向天线孔径长度与方位向采样率决定, 其中, \(L_a\) 直接决定方位向分辨率上限 \(ΔR_a\), \(F_{sa}\) 决定了能多大程度地恢复方位向分辨率为 \(ΔR_a\) 场景数据. 即使是过采样, 恢复后的最大分辨率仍然为 \(ΔR_a\), 但若是欠采样, 恢复后的分辨率将小于 \(ΔR_a\).

距离向的分辨率由距离向带宽和采样率决定, 其中, \(Br = |K_r|T_P\) 决定了距离向分辨率上限 \(ΔR_r\), \(F_{sr}\) 决定了能多大程度地恢复方位向分辨率为 \(ΔR_a\) 场景数据. 即使是过采样, 恢复后的最大分辨率仍然为 \(ΔR_r\), 但若是欠采样, 恢复后的分辨率将小于 \(ΔR_r\).

Imaging result of RDA.

图 9.7 Imaging result of RDA.

Imaging result of RDA. \(F_{sa}=100Hz\), \(N_{sa}=256\), \(L_a=6m\), \(F_{sr}=60e6Hz\), \(N_{sr}=320\), \(K_r=10e12Hz/s\), \(T_p=2.5e-6s\)

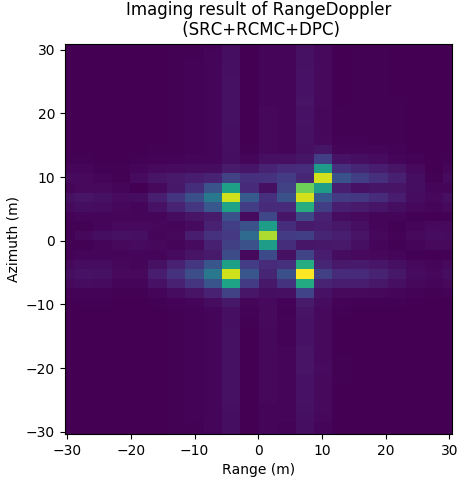
Imaging result of RDA.

图 9.8 Imaging result of RDA.

Imaging result of RDA. \(F_{sa}=100Hz\), \(N_{sa}=256\), \(L_a=3m\), \(F_{sr}=60e6Hz\), \(N_{sr}=320\), \(K_r=20e12Hz/s\), \(T_p=2.5e-6s\)

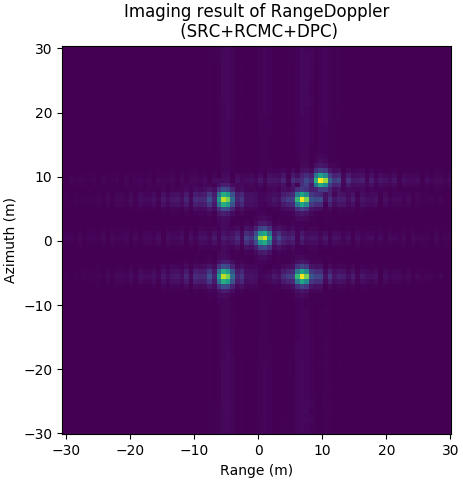
Imaging result of RDA.

图 9.9 Imaging result of RDA.

Imaging result of RDA. \(F_{sa}=200Hz\), \(N_{sa}=1024\), \(L_a=1.5m\), \(F_{sr}=240e6Hz\), \(N_{sr}=1280\), \(K_r=40e12Hz/s\), \(T_p=25e-6s\)

9.1.4. 距离徙动校正

设置斜视角 \(\theta_s = 8.5^°\), 调频率 \(K_r=20e12, L_a=3.0, L_r=12\), 方位向采样率 \(F_{sa}=100Hz\), 距离向采样率 \(F_{sr}=60MHz\), 目标位置 \((0, 0)\), 目标强度均为1. 分析距离徙动校正的效果, 分析不同大小的 \(\rm{sinc}\) 插值核 \(r=4, 8, 32\) 的影响.

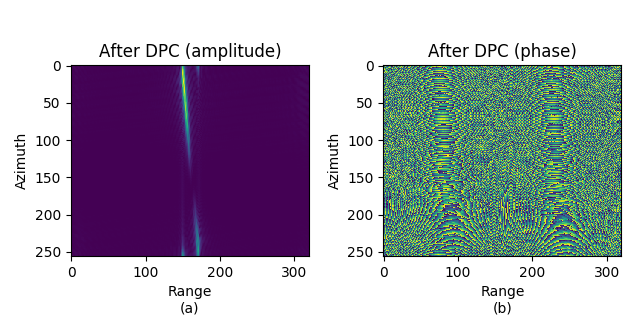
图 9.10 显示的是二次距离压缩及多普勒相位补偿后的结果, 即为进行距离徙动校正, 图 9.11, 图 9.12, 图 9.13 为 \(\rm{sinc}\) 插值核大小分别为 \(r=4, 8, 32\) 的时的距离徙动校正后的结果. 可见, 经过插值核越大, 距离徙动校正越精确.

After RC SRC, DPC

图 9.10 After RC SRC, DPC

After RC SRC, DPC

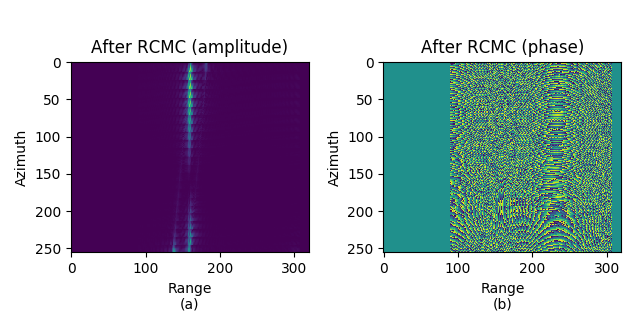
After RC SRC, DPC, RCMC

图 9.11 After RC SRC, DPC, RCMC. \(\rm sinc\) interpolation, \(r=4\).

After RC SRC, DPC, RCMC. \(\rm sinc\) interpolation, \(r=4\).

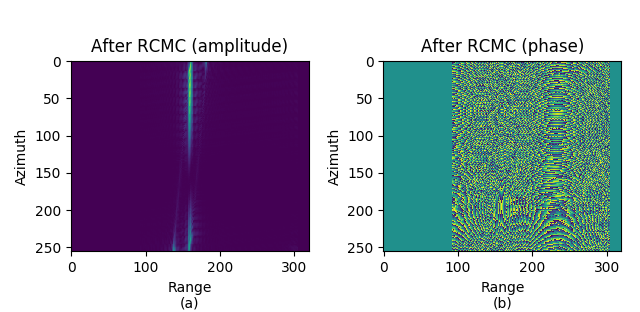
After RC SRC, DPC, RCMC.

图 9.12 After RC SRC, DPC, RCMC. \(\rm sinc\) interpolation, \(r=8\).

After RC SRC, DPC, RCMC. \(\rm sinc\) interpolation, \(r=8\).

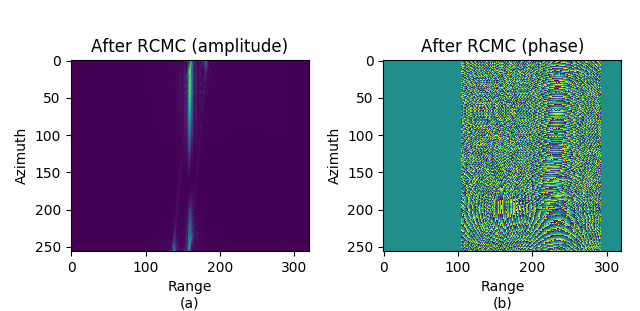
After RC SRC, DPC, RCMC.

图 9.13 After RC SRC, DPC, RCMC. \(\rm sinc\) interpolation, \(r=32\).

After RC SRC, DPC, RCMC. \(\rm sinc\) interpolation, \(r=32\).

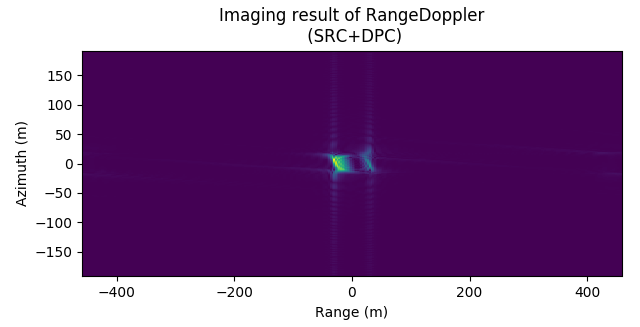
图 9.14 给出了无距离徙动校正条件下, 距离多普勒成像算法的成像结果, 由图可见, 距离徙动现象很明显, 同一目标分布在不同距离与方位单元. 图 9.15, 图 9.16, 图 9.17 为 \({\rm sinc}\) 插值核分别为 \(4,8,32\) 的条件下, 距离多普勒算法的成像结果, 对比 图 9.14 - 图 9.17, 可以发现, 基于 \(\rm sinc\) 插值的距离徙动算法校正效果明显, 且插值核越大, 距离徙动校正越精确.

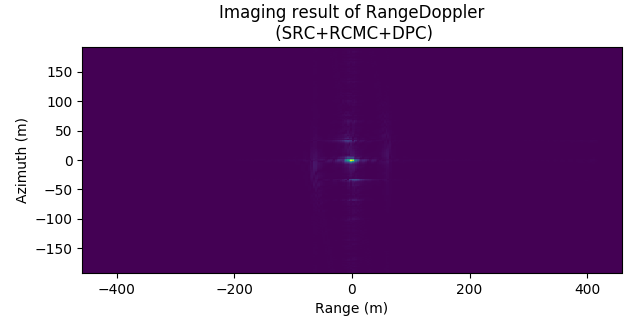
Imaging results of RDA (Without RCMC)

图 9.14 Imaging result of RDA.

Imaging result of RDA. Without RCMC.

Imaging results of RDA

图 9.15 Imaging result of RDA. \(\rm sinc\) interpolation (\(r=4\)).

Imaging result of RDA. \(\rm sinc\) interpolation (\(r=4\)).

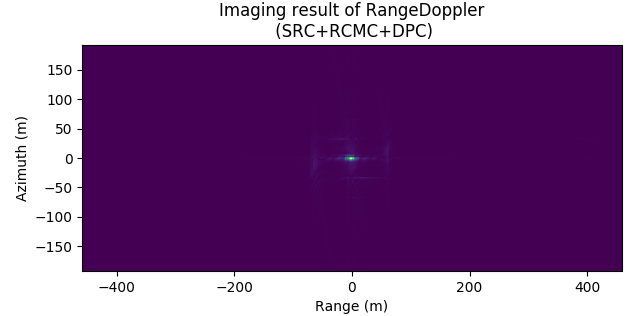
Imaging results of RDA

图 9.16 Imaging result of RDA. \(\rm sinc\) interpolation (\(r=8\)).

Imaging result of RDA. \(\rm sinc\) interpolation (\(r=8\)).

Imaging results of RDA

图 9.17 Imaging result of RDA. \(\rm sinc\) interpolation (\(r=32\)).

Imaging result of RDA. \(\rm sinc\) interpolation (\(r=32\)).