2.4. SAR回波信号及其性质

2.4.1. SAR回波信号

假设, 在距离向雷达发射信号为:

\[s_t(\tau) = p(\tau){\rm exp}(j2\pi f_0 \tau), \]

其中, \(f_0\) 为中心频率, \(\tau\) 是距离向时间, 也称快时间. \(p(\tau)\) 为线性调频信号，通常为

\[p(\tau) = w_r(\tau){\rm exp}(j\pi K_r \tau^2), \]

其中, \(K_r\) 为距离向调频率, \(T_p\) 为脉冲持续时间, \(w_r(\tau)={\rm rect}\left(\frac{\tau}{T_p}\right)\) 为脉冲包络.

在方位向, 接收信号的强度可以表示为方位时间的函数 1 :

\[w_a(\eta) = P^2_a\left(\theta(\eta)\right) = {\rm sinc}^2\left(\frac{0.886\theta(\eta)}{\beta_{bw}}\right), \]

其中, \(\theta(\eta)\) 为方位向 \(\eta\) 时刻斜距平面内测得的 (slant range) 与视线的夹角 (即 \(\eta\) 时刻目标与波束中心线的夹角, 不是斜视角, 显然目标处于波束中心时, 信号强度最大), \({\beta_{bw}} = 0.886\lambda/L_a\) 为方位向波束宽度, \(L_a\) 为天线方位向宽度.

以零多普勒时间 ( Zero Doppler Time ) 为参考, 记 \(\eta_c\) 为波束中心经过目标的时刻, 在斜视角不为零时, \(\eta_c\) 不为零 ( 前视时 \(\eta_c < 0\) , 后视时 \(\eta_c > 0\) )

\[\eta_c = - \frac{R_0{\rm tan}\theta_{r,c}}{V_r} = -\frac{R(\eta_c){\rm sin}\theta_{r,c}}{V_r} = - \frac{R_0{\rm tan}\theta_{s,c}}{V_g} = -\frac{R(\eta_c){\rm sin}\theta_{s,c}}{V_g}. \]

其中, \(R(\eta_c)\) 为目标被波束中心线照射时, 雷达与目标的斜距, \(\theta_{s,c}\) 为 \(\eta_c\) 时刻 \(\theta_s\) 的值.

注解

多普勒中心频率是指 \(\eta =\eta_c\) 时刻的多普勒频率

\[\begin{aligned} f_{\eta_c} &= -\frac{2}{\lambda}\frac{{\rm d}R(\eta)}{{\rm d}\eta}\Big |_{\eta=\eta_c} \\ &= -\frac{2V_r^2\eta_c}{\lambda R(\eta_c)} \\ &= \frac{2V_r {\rm sin}\theta_{r,c}}{\lambda} \\ &= \frac{2V_s {\rm sin}\theta_{s,c}}{\lambda}, \end{aligned} \]

其中, \(\theta_{s,c}, \theta_{r,c}\) 分别为 \(\eta_c\) 时刻, 基于轨道几何与直线几何的斜视角(参见《合成孔径雷达成像算法与实现》p84). 且 \(\theta_s, \theta_r\) 与方位向慢时间的关系为

\[\begin{aligned} {\sin}\theta_s &= \frac{Y_g}{R(\eta)}=-\frac{V_g\eta}{R(\eta)} \\ {\sin}\theta_r &= \frac{Y_r}{R(\eta)}=-\frac{V_r\eta}{R(\eta)} \end{aligned} \]

其中, \(V_g, \theta_s, Y_g\) 为地球弯曲几何中的变量, \(V_r, \theta_r, Y_r\) 为直线几何中的变量, 且有 \(\theta_r=\frac{V_r}{V_g}\theta_s=\frac{V_s}{V_r}\theta_s\). 对于机载SAR, 两种几何模型之间的差异可以忽略, 等效为直线几何.

低斜视角时, \(f_{\eta_c} \thickapprox -K_a\eta_c\).

这种情况下 \(\theta(\eta) = \theta_s -\theta_{s,c}\) , 且有

\[w_a(\eta-\eta_c) = P^2_a(\theta_s -\theta_{s,c}) \thickapprox P^2_a\left( {\rm arctan}\left(\frac{V_g(\eta-\eta_c)}{R_0}\right) \right). \]

其中, \(V_g\) 为波束覆盖面沿着地球表面移动的速度, 设 \(V_s\) 为SAR平台沿轨道的运行的速度, 即平台实际物理速度; \(V_r\) 为等效雷达速度, 即按两点间直线距离计算出的等效的速度, 则

\[V_r \thickapprox \sqrt{V_sV_g}, V_g < V_r < V_s. \]

时刻 \(\eta\) 雷达与目标的斜距可表示为:

\[R^2(\eta) = R_0^2 + V_r^2\eta^2. \]

接收的回波信号为二维的线性调频信号, 点目标回波表达式为:

(2.34)\[\begin{aligned} s(\eta, \tau) &= g(\eta, \tau) w_a(\eta-\eta_c) w_r\left(\tau-2R(\eta)/c\right) \\ &\quad {\rm exp}\left(2\pi f_0 (\tau-2R(\eta)/c) + \pi K_r\left(\tau-2R(\eta)/c\right)^2 \right\} \end{aligned} \]

2.4.2. 回波信号解调

载频不含目标信息, 解调便是将天线接收的信号中的载频成分移除. 在雷达接收系统中, 常采用正交解调的方法, 其原理图见 图 2.72 . 天线接收的信号 ① 分别与 \({\rm cos}(2πf_c t)\), \(-{\rm sin}(2πf_c t)\) 相乘将有用信号与载频信号分离, 得到信号 ② 和 ③; 分离开的信号经低通滤波滤出高频(载频)信号, 从而得到有用信号 ④ 和 ⑤; 信号 ④ 和 ⑤ 分别作为实部虚部合成复数信号 ⑥, ⑦ 为 ⑥ 的离散化采样形式.

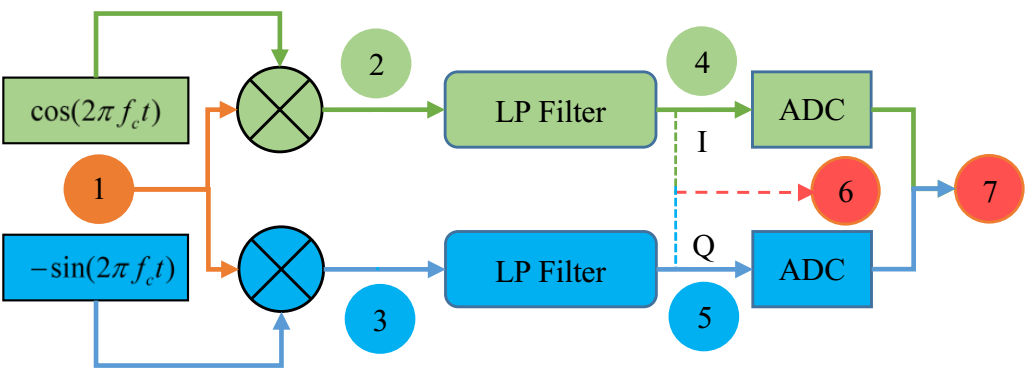
图 2.72 SAR IQ Demodulation

① \({\rm cos}\left(2\pi f_c\tau - \frac{4\pi f_c R(\eta)}{c} + \pi K_r \left(\tau-\frac{2R(\eta)}{c}\right)^2\right) = {\rm cos}\left(2\pi f_c \tau+ \phi(\eta, \tau)\right)\)

② \(\frac{1}{2}{\rm cos}[\phi(\eta, \tau)] + \frac{1}{2}{\rm cos}[4\pi f_c\tau+ \phi(\eta, \tau)]\)

③ \(\frac{1}{2}{\rm sin}[\phi(\eta, \tau)] + \frac{1}{2}{\rm sin}[4\pi f_c\tau+ \phi(\eta, \tau)]\)

④ \(\frac{1}{2}{\rm cos}[\phi(\eta, \tau)]\)

⑤ \(\frac{1}{2}{\rm sin}[\phi(\eta, \tau)]\)

⑥ \(\frac{1}{2}{\rm exp}\{j\phi(\eta, \tau)\} = \frac{1}{2}{\rm exp}\left\{-j\frac{4\pi f_c R(\eta)}{c} + j\pi K_r \left(\tau-\frac{2R(\eta)}{c}\right)^2\right\}\)

式.2.34 解调后的SAR信号可以表示为:

(2.35)\[\begin{aligned} s(\eta, \tau) &= g(\eta, \tau) w_a(\eta-\eta_c) w_r\left(\tau-2R(\eta)/c\right) \\ &\quad {\rm exp}\left\{ -j4\pi f_0 R(\eta)/c + j\pi K_r\left(\tau-2R(\eta)/c\right)^2 \right\} \end{aligned} \]

其中系数 \(g(\eta, \tau)=G^{\prime}{\rm exp}(j\phi)\) 为复常数, \(G^{\prime}\) 为强度. 然后对距离向信号进行采样，可以得到SAR原始数据. 上式表示的是从场景反射系数 \(g(\eta, \tau)\) 的点目标接收到的经解调后的SAR基带信号, 也是SAR系统进行记录与下传的信号, 称为 SAR原始数据 (SAR raw data), SAR信号数据 (SAR signal data), SAR相位历史数据 (SAR phase history data ).

若场景中含 \(N\) 个目标, 则接收到的SAR数据为各目标回波的叠加

\[s(\eta, \tau) = \sum_{i=1}^N s_i(\eta, \tau) \]

若考虑系统噪声, 则有

\[s(\eta, \tau) = \sum_{i=1}^N s_i(\eta, \tau) + n(\eta, \tau) \]

提示

方位向多普勒带宽, 调频率及目标照射时间，参见 1 p93 页.

2.4.3. SAR 冲击响应

SAR的回波信号可以看作是地面反射率 \(g(\eta, \tau)\) 与雷达系统冲激响应 \(h(\eta, \tau)\) 进行二维卷积, 即:

(2.36)\[\begin{aligned} s(\eta, \tau) &=g(\eta, \tau) \otimes h(\eta, \tau) + n( \eta, \tau) \\ &= \iint g(u, v)⋅h(\eta -u, \tau -v){\rm d}u{\rm d}v + n( \eta, \tau) \\ &= g(\eta, \tau) w_a(\eta-\eta_c) w_r\left(\tau-2R(\eta)/c\right)\\ &\quad {\rm exp}\left\{ -j4\pi f_0 R(\eta)/c + j\pi K_r\left(\tau-2R(\eta)/c\right)^2 \right\} + n(\eta, \tau) \end{aligned} \]

其中, \(n(\tau, \eta)\) 为系统噪声. 雷达二维冲激响应为

(2.37)\[\begin{aligned} h(\eta, \tau) &= w_a(\eta-\eta_c) w_r\left(\tau-2R(\eta)/c\right) \\ &\quad {\rm exp}\left\{ -j4\pi f_0 R(\eta)/c + j\pi K_r\left(\tau-2R(\eta)/c\right)^2 \right\} \end{aligned} \]

因此不管是点目标还是面目标都可以通过SAR的接收信号的一般模型求得回波表达式, SAR 的成像处理过程, 其实际上也是一个通过解卷积从回波信号中最大程度地、无失真地提取地表的后向散射系数的二维分布.

冲激响应 \(h(\eta, \tau)\) 可以表示成距离向上的冲激响应 \(h_r(\eta, \tau)\) 和方位向上的冲激响应 \(h_a(\eta, \tau)\) 之积, 即

\[h(\eta, \tau) = h_a(\eta,\tau) h_r(\eta,\tau) = h_r(\eta,\tau) h_a(\eta,\tau) \]

则 式.2.36 可以表示为地面反射系数与两个方向上的冲激响应的一维级联卷积

(2.38)\[\begin{aligned} s(\eta, \tau) &= g(\eta, \tau) \otimes h(\eta,\tau) \\ &= g(\eta, \tau) * h_a(\eta,\tau)* h_r(\eta,\tau)\\ &= g(\eta, \tau) * h_r(\eta,\tau)* h_a(\eta,\tau) \end{aligned} \]

其中, \(\otimes\) 表示二维卷积, \(*\) 表示一维卷积.

方位向上的冲激响应为

(2.39)\[\begin{aligned} h_a(\eta, \tau) &= w_a(\eta-\eta_c) \\ &\quad {\rm exp}\left\{ -j4\pi f_0 R(\eta)/c \right\} \end{aligned} \]

距离向上的冲激响应为

(2.40)\[\begin{aligned} h_r(\eta, \tau) &= w_r\left(\tau-2R(\eta)/c\right) \\ &\quad {\rm exp}\left\{j\pi K_r\left(\tau-2R(\eta)/c\right)^2 \right\} \end{aligned} \]

若用 \(S, G, H\) 分别表示SAR回波的频域信号, 地面目标后向散射系数的频域信号, 二维冲激响应的频域信号, 则

(2.41)\[S = GH. \]

式.2.41 说明, 可以通过频域相乘来简化和加速SAR回波仿真过程. 其过程可以简要叙述为

注解

频域SAR信号模拟生成

输入: 时域场景反射系数矩阵 \({\bm G}_{H\times W}\), 时域二维冲激响应矩阵 \({\bm H}\)

输出: 时域SAR回波信号矩阵 \({\bm S}_{N_a\times N_r}\)

Step 1: 对时域场景反射系数矩阵 \({\bm G}_{H\times W}\) 做二维傅里叶变换, 得到其频域二维形式 \(G = {\rm FFT}({\bm G})\)

Step 2: 对时域二维冲激响应矩阵 \({\bm H}\) 做二维傅里叶变换, 得到其频域二维形式 \(H = {\rm FFT}(\bm H)\) Step3: 通过频域相乘得到频域SAR回波信号 \(S = GH\)

Step4: 通过逆傅里叶变换得到时域SAR回波信号矩阵 \({\bm S} = {\rm IFFT}(S)\)

2.4.4. 小斜视SAR回波信号的频谱

在小斜视模式下, 方位 \(\eta\) 时刻, 雷达与目标间的瞬时斜距可以近似表示为

\[R(\eta) = \sqrt{R_0^2 + V_r^2 \eta^2} \approx \]

距离维频谱

方位维频谱

距离多普勒域频谱

二维频谱

Footnotes

1(1,2)

参见 《合成孔径雷达成像——算法与实现》p91 页.