4.3. 调频变标成像¶
4.3.1. 调频变标原理¶
Chirp Scaling
4.3.2. 调频变标成像¶
CSA方法概览¶
注解
Chirp Scaling 算法
输入: SAR原始回波数据矩阵 \({\bm S}\), SAR平台参数
输出: SAR复数图像
Step1. 对时域回波数据 \({\bm S}\) 作方位FFT, 变换到距离多普勒域 \({\rm FFT}({\bm S})\)
Step2. 通过相位相乘实现调频变标操作, 变标方程为 式.4.9
Step3. 对Step2中结果做FFT变换到二维频域
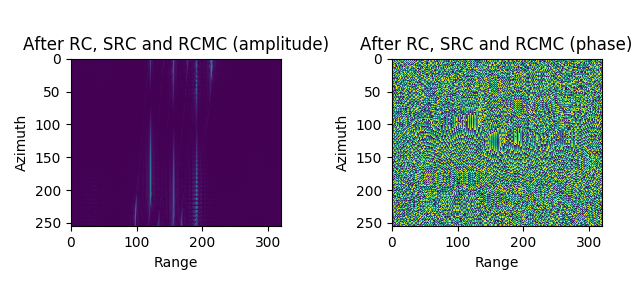
Step4. 完成距离压缩, 二次距离压缩和一致RCMC
Step5. 做距离向 IFFT 将数据变换回距离多普勒域
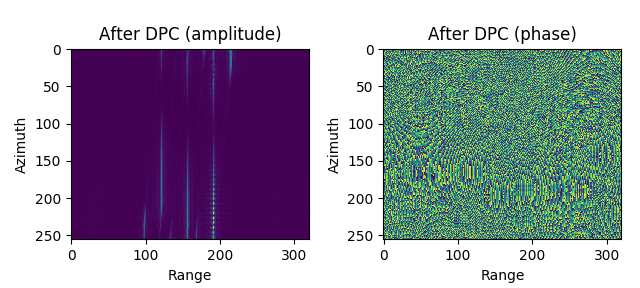
Step6. 与随距离变化的匹配滤波器(含相位校正)相乘, 实现方位压缩
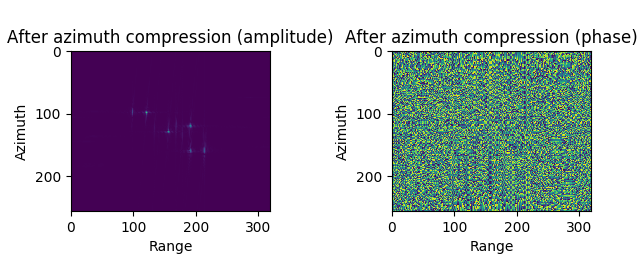
Step7. 通过方位向IFFT将数据变换回二维时域, 即复数SAR图像.
调频变标¶
线性调频变标方程为
其中, \({\tau^\prime} = \tau- \frac{2R_{ref}}{cD(f_{\eta}, V_{r_{ref}})}\), \(K_m = \frac{K_r}{1-K_r\frac{cR_0 f^2_{\eta}}{2V_r^2f_0^3 D^3(f_{\eta, V_r})}}\), \(D(f_{\eta}, V_r) = \sqrt{1-\frac{c^2f_{\eta}^2}{4V_r^2f_0^2}}\), 方位频率 \(f_{\eta}\) 处的时间平移是距离时间的函数
非线性调频变标方程 [1] p209
距离压缩与距离徙动校正¶
距离匹配滤波器仍为 式.4.2 所示的匹配滤波器
有关二次距离压缩的内容参见 距离多普勒成像 中的 大斜视下的RDA.
整体RCM为
一致RCM为
方位向处理¶
[1] p209
方位向包含三部分处理: 方位向匹配滤波, 附加相位校正, 方位向IFFT.
通过距离向IFFT完成距离向的处理, 得到距离多普勒域信号
4.3.3. 实验与分析¶
真实数据实验¶
实验数据¶
实验所采用数据为 RADARSAT1 卫星上的合成孔径雷达获取的温哥华地区的图像. 具体介绍参见 RADARSAT 产品介绍 小节.
实验说明¶
分析RDA算法中二次距离压缩与距离徙动补偿的影响.
实验代码¶
Python实现代码, 参见文件 demo_RADARSAT1.py .
实验结果¶
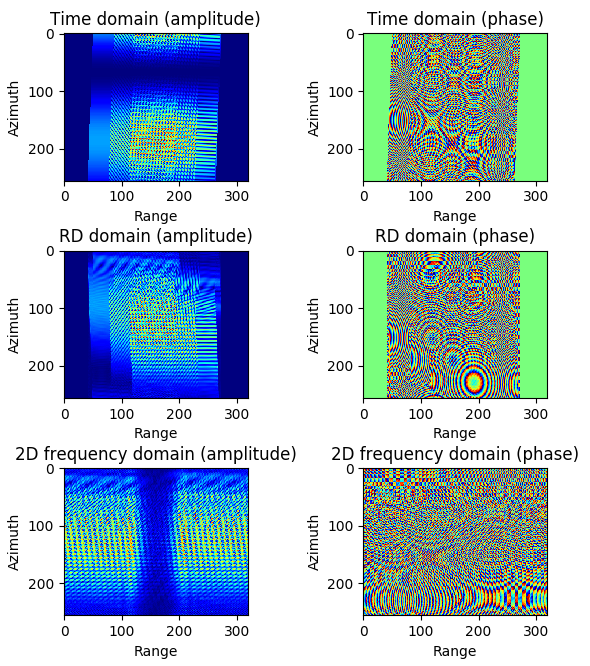
RADARSAT1 获取的史丹利公园的SAR数据幅度与相位
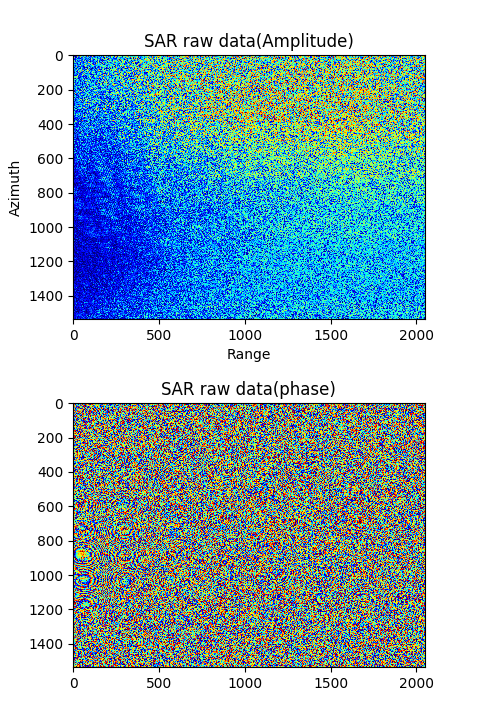
图 4.50 SAR raw data amplitude and phase of Stanley Park.¶
SAR raw data amplitude and phase of Stanley Park.
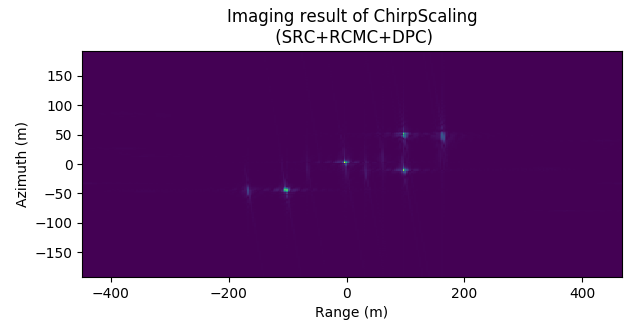
CSA 成像结果

图 4.51 Imaging result of CSA (without SRC, without RCMC)¶
Imaging result of CSA (without SRC, without RCMC)

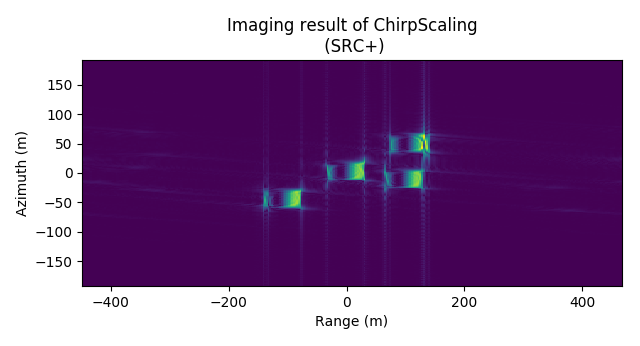
图 4.52 Imaging result of CSA (with SRC, without RCMC)¶
Imaging result of CSA (with SRC, without RCMC)

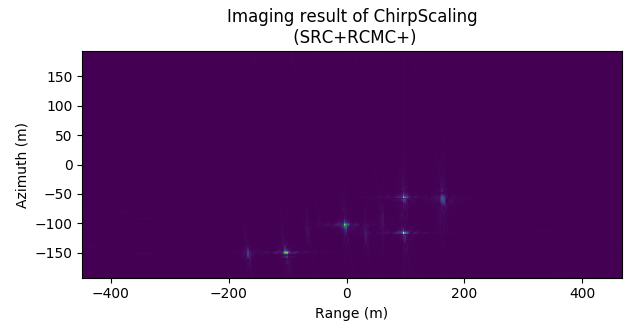
图 4.53 Imaging result of CSA (without SRC, with RCMC)¶
Imaging result of CSA (without SRC, with RCMC)