4.4. 正则化成像方法

4.4.1. 正则化成像

SAR imaging process can be formulated as

${\bm s} = {\bm A}{\bm g},$

where, ${\bm s}$ is the $MN\times 1$ recieved SAR raw data vector in phase history domain, $\bm g$ is the $HW \times 1$ reflection vector of scene, and $\bm A$ represents the the mapping from scene to SAR raw data.

Given $\bm s, \bm A$ , regularization methods try to reconstruct $\bm g$ by minmizing

$\mathop {\rm min}\limits_{\bm{g}} {\left\| {{\bm{Ag}} - {\bm{s}}} \right\|_2} + \lambda |{\bm{g}}{|_p},$

where, $\lambda$ is the balance factor, and $|\cdot|_p$ is the $\ell_p$ norm.

Note that, if ${\bm s, A, g} \in {\mathbb C}$ , the problem changes to

${\mathop{\rm Re}\nolimits} ({\bm{s}}) + j{\rm Im}({\bm{s}}) = {\rm Re}({\bm{Ag}}) + j{\mathop{\rm Im}\nolimits} ({\bm{Ag}})$

so we have:

$\left[ {\begin{array}{ccc} {{\mathop{\rm Re}\nolimits} ({\bm{s}})}\\ {{\mathop{\rm Im}\nolimits} ({\bm{s}})} \end{array}} \right] = \left[ {\begin{array}{ccc} {{\mathop{\rm Re}\nolimits} ({\bm{A}})}&{ - {\mathop{\rm Im}\nolimits} ({\bm{A}})}\\ {{\rm Im}({\bm{A}})}&{{\mathop{\rm Re}\nolimits} ({\bm{A}})} \end{array}} \right]\left[ {\begin{array}{ccc} {{\mathop{\rm Re}\nolimits} ({\bm{g}})}\\ {{\mathop{\rm Im}\nolimits} ({\bm{g}})} \end{array}} \right]$

4.4.2. 实验与分析

实验说明

• 仿真场景大小: $32 \times 32$

• 回波矩阵大小: $32 \times 32$

• 稀疏表示字典: 无, DCT , DWT

• 优化方法: Lasso , OMP

仿真点目标场景图及仿真生成点SAR原始数据幅度与相位图如下:

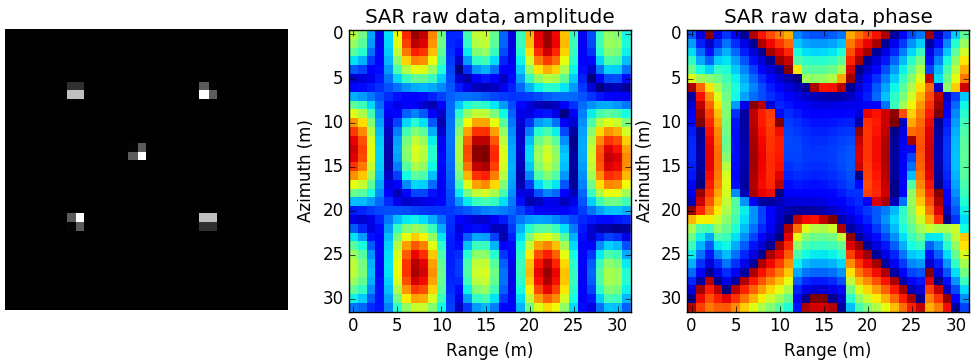
图 4.55 仿真点目标场景图, 仿真SAR原始数据幅度相位图

仿真船只场景图及仿真生成点SAR原始数据幅度与相位图如下:

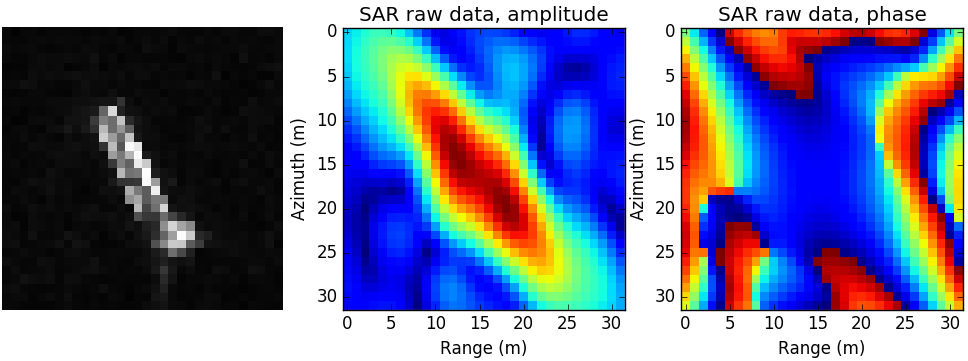
图 4.56 仿真船只场景图及仿真生成点SAR原始数据幅度与相位图如下

仿真荷花场景图及仿真生成点SAR原始数据幅度与相位图如下:

图 4.57 仿真荷花场景图及仿真生成点SAR原始数据幅度与相位图如下

实验代码

iprs2.0 demo_regular_sar.py

实验结果

点目标结果

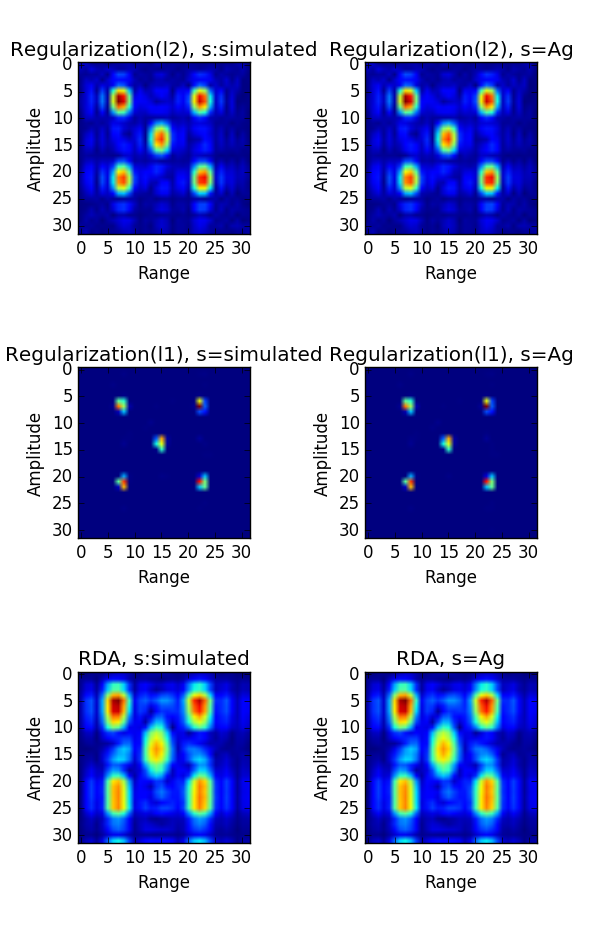
图 4.58 Imaging result of $\ell_1, \ell_2$ regularization and RDA. $\lambda=0.001$ , max iter 1000

图 4.59 Imaging result of $\ell_1, \ell_2$ regularization and RDA. $\lambda=0.001$ , max iter 1000

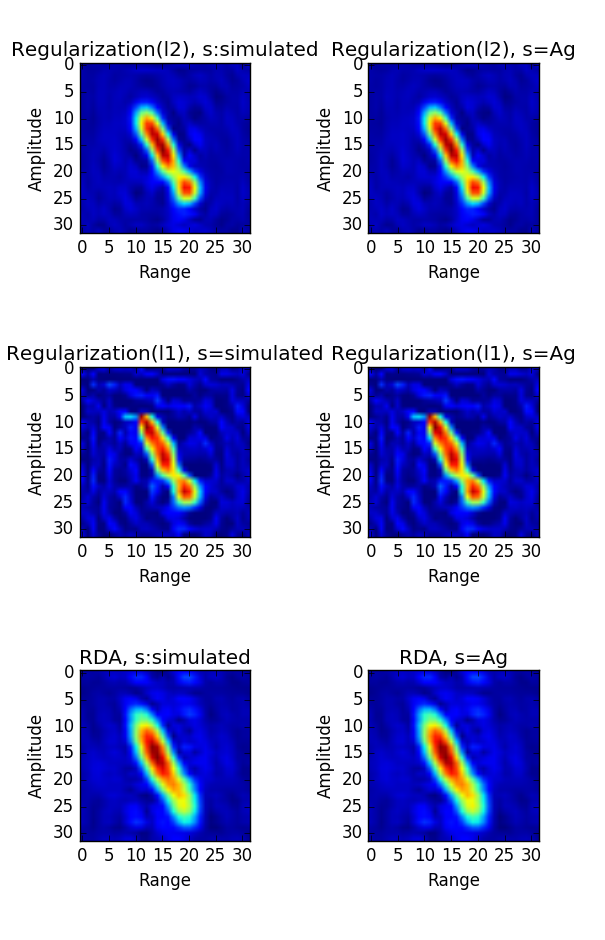
图 4.60 Imaging result of $\ell_1, \ell_2$ regularization and RDA. $\lambda=0.001$ , max iter 1000

• 运行时间:

• 重构误差: