结构分析
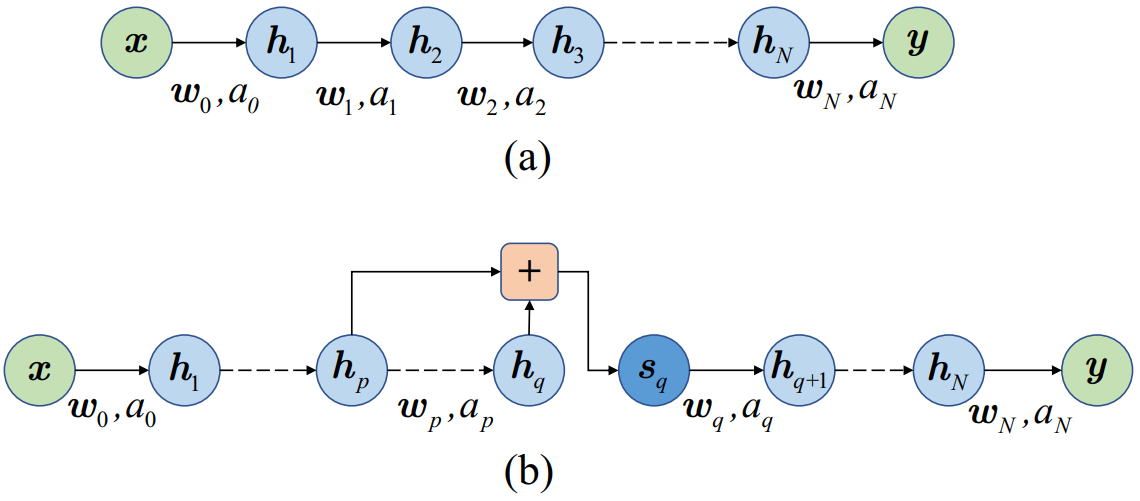
如 图 2.35 所示, \({\bm w}_n, a_n\) 分别表示第 \(n\) 层的权重与激活函数, \({\bm x}\) 为输入, \({\bm y}\) 为神经网络输出. 图 2.35 (a) 所示为无跳跃连接的网络结构, 图 2.35 (b) 所示为前向跳跃连接结构示意图, 其中, 第 \(p\) 层的输出跳跃连接至第 \(q\) 层的输出, 加和后送入下一层. 网络的前向传播过程可以表示为 式.2.20.
(2.20)\[\begin{aligned}
{\bm y} &= a_N({\bm w}_N{\bm h}_N) \\
&\ \ \vdots \\
{\bm h}_{q+1} &= a_q({\bm w}_q{\bm s}_q) \\
{\bm s}_q &= {\bm h}_p + {\bm h}_q \\
&\ \ \vdots \\
{\bm h}_{p+1} &= a_p({\bm w}_p{\bm h}_p) \\
&\ \ \vdots \\
{\bm h}_2 &= a_1({\bm w}_1{\bm h}_1) \\
&\ \ \vdots \\
{\bm h}_1 &= a_0({\bm w}_0{\bm x})
\end{aligned}
\]
梯度传播分析
利用链式求导法则, 图 2.35 (a) 所示传统神经网络的梯度传播过程可以表示为 式.2.21
(2.21)\[\begin{aligned}
\frac{\partial L}{\partial {\bm w}_N} &= \frac{\partial L}{\partial {\bm y}}\times \frac{\partial {\bm y}}{\partial {\bm w}_N}\\
\frac{\partial L}{\partial {\bm w}_{N-1}} &= \frac{\partial L}{\partial {\bm y}}\times \frac{\partial {\bm y}}{\partial {\bm h}_N}\times \frac{\partial {\bm h}_N}{\partial {\bm w}_{N-1}}\\
&\ \ \vdots \\
\frac{\partial L}{\partial {\bm w}_q} &= \frac{\partial L}{\partial {\bm y}}\times \frac{\partial {\bm y}}{\partial {\bm h}_N}\times \frac{\partial {\bm h}_N}{\partial {\bm h}_{N-1}}\times \cdots \times \frac{\partial {\bm h}_{q+1}}{\partial {\bm w}_q}\\
&\ \ \vdots \\
\frac{\partial L}{\partial {\bm w}_p} &= \frac{\partial L}{\partial {\bm y}}\times \frac{\partial {\bm y}}{\partial {\bm h}_N}\times \frac{\partial {\bm h}_N}{\partial {\bm h}_{N-1}}\times \cdots \times \frac{\partial {\bm h}_{q+1}}{\partial {\bm h}_q}\times \cdots \times \frac{\partial {\bm h}_{p+1}}{\partial {\bm w}_p}\\
&\ \ \vdots \\
\frac{\partial L}{\partial {\bm w}_1} &= \frac{\partial L}{\partial {\bm y}}\times \frac{\partial {\bm y}}{\partial {\bm h}_N}\times \frac{\partial {\bm h}_N}{\partial {\bm h}_{N-1}}\times \cdots \times \frac{\partial {\bm h}_2}{\partial {\bm w}_1}\\
\frac{\partial L}{\partial {\bm w}_0} &= \frac{\partial L}{\partial {\bm y}}\times \frac{\partial {\bm y}}{\partial {\bm h}_N}\times \frac{\partial {\bm h}_N}{\partial {\bm h}_{N-1}}\times \cdots \times \frac{\partial {\bm h}_2}{\partial {\bm h}_1}\times \frac{\partial {\bm h}_1}{\partial {\bm w}_0}\\
\end{aligned}
\]
同样地, 根据链式求导法则, 图 2.35 (b) 所示含跳跃连接的神经网络的梯度传播过程可以表示为 式.2.22
(2.22)\[\begin{aligned}
\frac{\partial L}{\partial {\bm w}_N} &= \frac{\partial L}{\partial {\bm y}}\times \frac{\partial {\bm y}}{\partial {\bm w}_N}\\
\frac{\partial L}{\partial {\bm w}_{N-1}} &= \frac{\partial L}{\partial {\bm y}}\times \frac{\partial {\bm y}}{\partial {\bm h}_N}\times \frac{\partial {\bm h}_N}{\partial {\bm w}_{N-1}}\\
&\ \ \vdots \\
\frac{\partial L}{\partial {\bm w}_q} &= \frac{\partial L}{\partial {\bm y}}\times \frac{\partial {\bm y}}{\partial {\bm h}_N}\times \frac{\partial {\bm h}_N}{\partial {\bm h}_{N-1}}\times \cdots \times \frac{\partial {\bm h}_{q+1}}{\partial {\bm w}_q}\\
\frac{\partial L}{\partial {\bm w}_{q-1}} &= \frac{\partial L}{\partial {\bm y}}\times \frac{\partial {\bm y}}{\partial {\bm h}_N}\times \frac{\partial {\bm h}_N}{\partial {\bm h}_{N-1}}\times \cdots \times \frac{\partial {\bm h}_{q+1}}{\partial {\bm s}_{q}}\times \frac{\partial {\bm s}_{q}}{\partial {\bm h}_{q}}\times \frac{\partial {\bm h}_{q}}{\partial {\bm w}_{q-1}}\\
&\ \ \vdots \\
\frac{\partial L}{\partial {\bm w}_p} &= \frac{\partial L}{\partial {\bm y}}\times \frac{\partial {\bm y}}{\partial {\bm h}_N}\times \frac{\partial {\bm h}_N}{\partial {\bm h}_{N-1}}\times \cdots \times \frac{\partial {\bm h}_{q+1}}{\partial {\bm s}_{q}}\times \frac{\partial {\bm s}_{q}}{\partial {\bm h}_{p+1}} \times \frac{\partial {\bm h}_{p+1}}{\partial {\bm w}_p}\\
&\ \ \vdots \\
\frac{\partial L}{\partial {\bm w}_{p-1}} &= \frac{\partial L}{\partial {\bm y}}\times \frac{\partial {\bm y}}{\partial {\bm h}_N}\times \frac{\partial {\bm h}_N}{\partial {\bm h}_{N-1}}\times \cdots \times \frac{\partial {\bm h}_{q+1}}{\partial {\bm s}_{q}}\times \frac{\partial {\bm s}_{q}}{\partial {\bm h}_p} \times \frac{\partial {\bm h}_{p}}{\partial {\bm w}_{p-1}}\\
&\ \ \vdots \\
\frac{\partial L}{\partial {\bm w}_1} &= \frac{\partial L}{\partial {\bm y}}\times \frac{\partial {\bm y}}{\partial {\bm h}_N}\times \frac{\partial {\bm h}_N}{\partial {\bm h}_{N-1}}\times \cdots \times \frac{\partial {\bm h}_{q+1}}{\partial {\bm s}_{q}}\times \frac{\partial {\bm s}_{q}}{\partial {\bm h}_2} \times \frac{\partial {\bm h}_2}{\partial {\bm w}_1}\\
&\ \ \vdots \\
\frac{\partial L}{\partial {\bm w}_0} &= \frac{\partial L}{\partial {\bm y}}\times \frac{\partial {\bm y}}{\partial {\bm h}_N}\times \frac{\partial {\bm h}_N}{\partial {\bm h}_{N-1}}\times \cdots \times \frac{\partial {\bm h}_{q+1}}{\partial {\bm s}_{q}}\times \frac{\partial {\bm s}_{q}}{\partial {\bm h}_1} \times \frac{\partial {\bm h}_1}{\partial {\bm w}_0}\\
\end{aligned}
\]
当 \(k=p+1, p+2, \cdots, q\) 时, \(\frac{\partial {\bm s}_q}{\partial {\bm h}_k}=\frac{\partial {\bm s}_q}{\partial {\bm h}_q}\times \frac{\partial {\bm h}_q}{\partial {\bm h}_{q-1}} \times \cdots \times \frac{\partial {\bm h}_{k+1}}{\partial {\bm h}_k}\).
当 \(k=1, 2, \cdots, p\) 时, \(\frac{\partial {\bm s}_q}{\partial {\bm h}_k}=\frac{\partial {\bm s}_q}{\partial {\bm h}_p}\times \frac{\partial {\bm h}_p}{\partial {\bm h}_k} = \left(\frac{\partial {\bm h}_q}{\partial {\bm h}_p} + 1\right)\times \frac{\partial {\bm h}_p}{\partial {\bm h}_k} = \left(\frac{\partial {\bm h}_q}{\partial {\bm h}_{q-1}}\times \cdots \times \frac{\partial {\bm h}_{p+1}}{\partial {\bm h}_p} + 1\right)\times \frac{\partial {\bm h}_p}{\partial {\bm h}_{p-1}}\times \cdots \times \frac{\partial {\bm h}_{k+1}}{\partial {\bm h}_k}\).
注解
由 式.2.21 和 式.2.22 可知, 与传统不含跳跃连接的神经网络相比, 从第 \(p\) 层输出跳跃连接至第 \(q\) 层输出的跳跃神经网络的梯度在第 \(p+1\) 层到第 \(N\) 层保持不变, 在第 \(1\) 层到第 \(p\) 层的变大, 且增量为 \(\frac{\partial L}{\partial {\bm y}}\times \frac{\partial {\bm y}}{\partial {\bm h}_N}\times \frac{\partial {\bm h}_N}{\partial {\bm h}_{N-1}}\times \cdots \times \frac{\partial {\bm h}_{q+1}}{\partial {\bm s}_{q}}\times \frac{\partial {\bm h}_p}{\partial {\bm h}_{p-1}}\times \cdots \times \frac{\partial {\bm h}_{k+1}}{\partial {\bm h}_k}\), (\(k=1,2, \cdots, p\)).