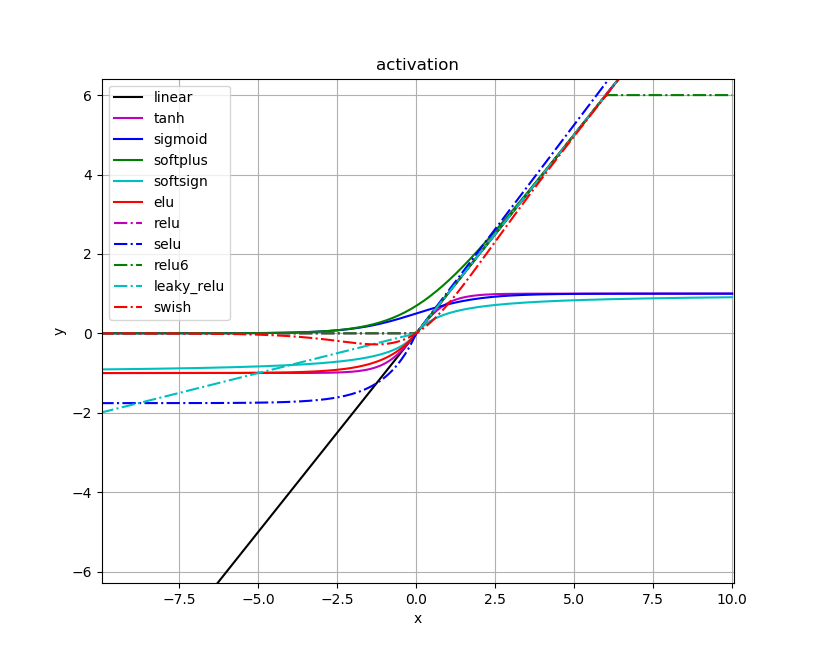
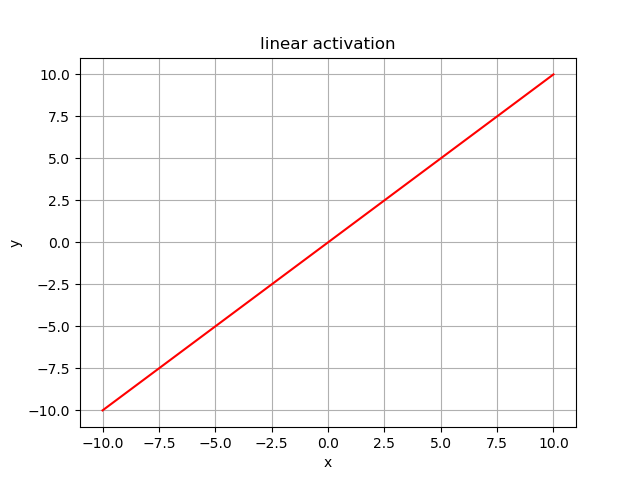
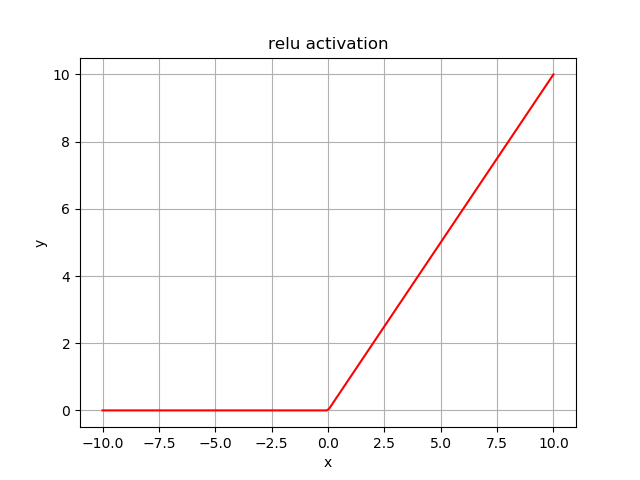
2.1. 激活函数单元¶
2.1.1. 什么是激活函数¶
2.1.2. 为什么要有激活函数¶
2.1.3. 经典激活函数分类¶
思维导图补充
tanh¶
函数表达式: \(y = {\rm tanh}(x) = {{e^{2x} - 1} \over {e^{2x} + 1}}\)
函数特性: 非线性, 存在梯度弥散
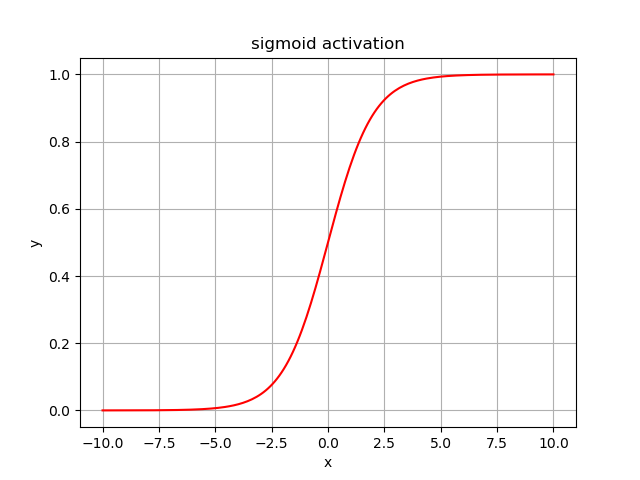
Sigmoid¶
函数表达式: \(y = {e^x \over {e^x + 1}}\)
函数特性: 非线性, 存在梯度弥散
softsign¶
函数表达式: \(\frac{x} {({\rm abs}(x) + 1)}\)
函数特性: 非线性
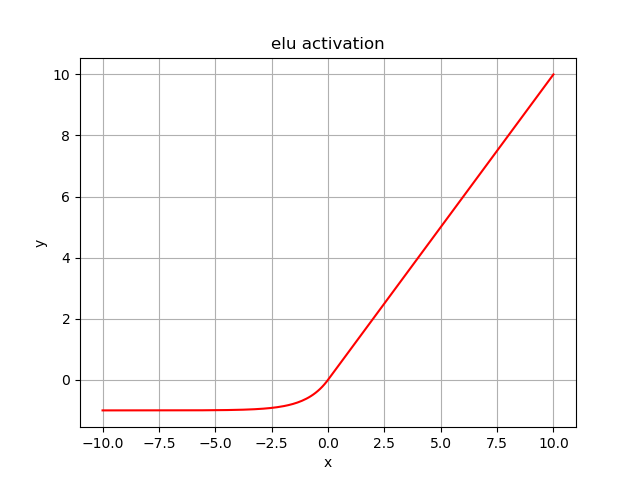
elu¶
函数表达式: \(y = \left\{ {\begin{array}{ccc}{x,\;\;\;\;\;\;\;\;\;x \ge 0}\\{{e^x} - 1,\;\;\;x < 0}\end{array}} \right.\)
函数特性: 非线性
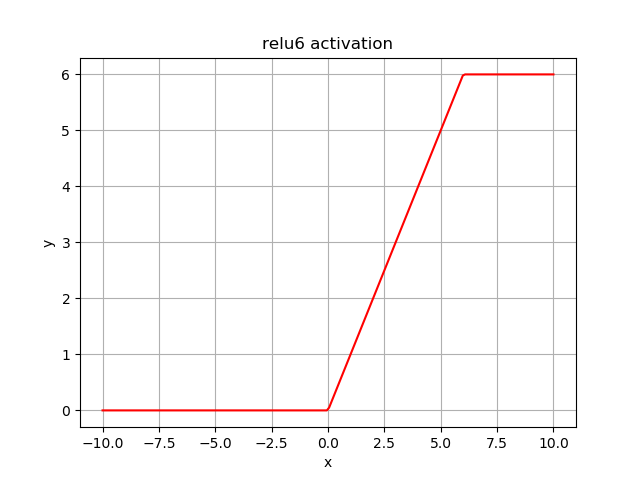
relu6¶
Convolutional Deep Belief Networks on CIFAR-10. A. Krizhevsky
函数表达式: \({\rm min}({\rm max}(x, 0), 6)\)
函数特性: 非线性+线性
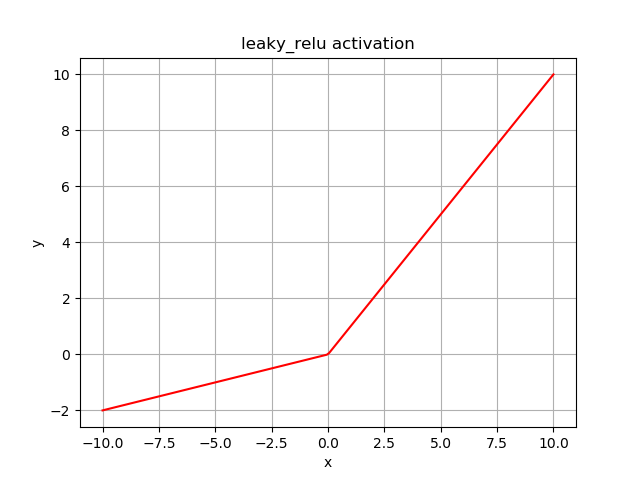
leaky relu¶
函数表达式: \(y = \left\{ {\begin{array}{ccc}{x,\;\;\;\;\;\;x \ge 0}\\{\alpha x,\;\;\;x < 0}\end{array}} \right.\)
函数特性: 非线性+线性
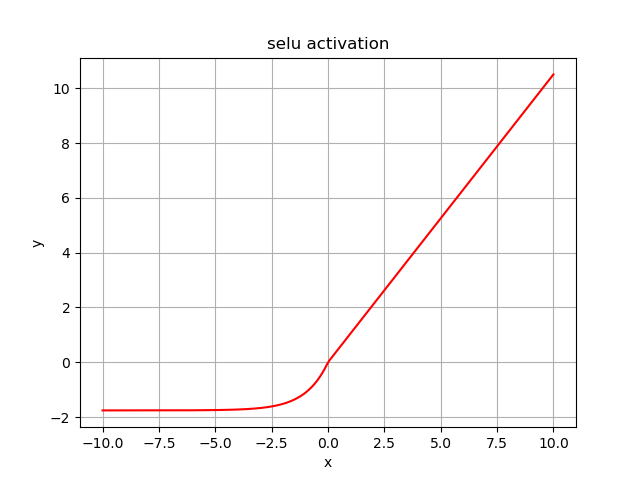
selu¶
函数表达式: \(y = \lambda \left\{ {\begin{array}{ccc}{x,\;\;\;\;\;\;\;\;\;\;\;\;\;x \ge 0}\\{\alpha ({e^x} - 1),\;\;\;\;x < 0}\end{array}} \right.\)
函数特性: 非线性, 自归一化
crelu¶
函数表达式: \(y = e^x \over (e^x + 1)\)
函数特性: 非线性, 存在梯度弥散
Swish¶
Searching for Activation Functions” (Ramachandran et al. 2017)
函数表达式: \(y = x\cdot {\rm sigmoid}(\beta x) = {e^{(\beta x)} \over {e^{(\beta x)} + 1}} \cdot x\)
函数特性: 非线性, 存在梯度弥散