2.2. 卷积单元

2.2.1. 经典卷积运算

经典二维卷积

设有 \(N_i\) 个二维卷积输入 \({\bm I} \in {\mathbb R}^{N_i × C_i \times H_i \times W_i}\), \(C_k \times C_i\) 个二维卷积核 \({\bm K} \in {\mathbb R}^{C_k \times C_i \times H_k \times W_k}\), \(N_o\) 个卷积输出记为 \({\bm O} \in {\mathbb R}^{N_o × C_o \times H_o \times W_o}\), 在经典卷积神经网络中, 有 \(C_k = C_o, N_o = N_i\), \({\bm K}\) 与 \(\bm I\) 间的二维卷积运算可以表示为

(2.12)\[\begin{aligned} {\bm O}_{n_o, c_o, :, :} &= \sum_{c_i=0}^{C_i-1} {\bm I}_{n_o, c_i, :,:} * {\bm K}_{c_o, c_i, :,:} \\ &= \sum_{c_i=0}^{C_i-1}{\bm Z}_{n_o, c_o, c_i, :, :} \end{aligned} \]

其中, \(*\) 表示经典二维卷积运算, 卷积核 \({\bm K}_{c_o, c_i, :,:}\) 与输入 \({\bm I}_{n_o, c_i, :,:}\) 的卷积结果记为 \({\bm Z}_{n_o, c_o, c_i, :, :}\in {\mathbb R}^{H_o \times W_o}\), 则

(2.13)\[{\bm Z}_{n_o, c_o, c_i, h_o, w_o} = \sum_{h=0}^{H_k-1}\sum_{w=0}^{W_k-1} {\bm I}_{n_o, c_i, h_o + h - 1, w_o + w - 1} \cdot {\bm K}_{c_o, c_i, h, w}. \]

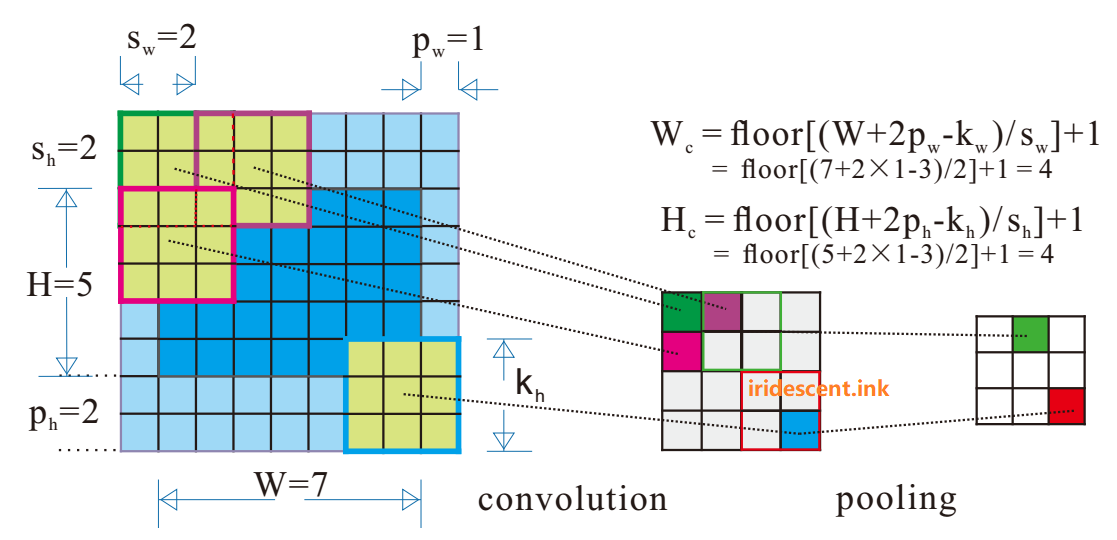
记卷积过程中, 高度与宽度维上填补(padding)大小为 \(H_p \times W_p\), 卷积步长为 \(H_s \times W_s\), 则卷积输出大小满足

(2.14)\[\begin{array}{ll} H_{o} &= \left\lfloor\frac{H_{i} + 2 \times H_p - H_k}{H_s} + 1\right\rfloor \\ W_{o} &= \left\lfloor\frac{W_{i} + 2 \times W_p - W_k}{W_s} + 1\right\rfloor \end{array} \]

警告

卷积神经网络中的卷积操作, 实际上是相关操作, 因为在运算过程中, 未对卷积核进行翻转操作, 卷积与相关的关系参见 卷积与相关 小节.

如 图 2.31 所示为二维卷积操作示意图.

卷积示意图

图 2.31 卷积示意图

卷积示意图

卷积与转置卷积

Deconvolution and Checkerboard Artifacts

经典膨胀二维卷积运算

设有 \(N_i\) 个二维卷积输入 \({\bm I} \in {\mathbb R}^{N_i × C_i \times H_i \times W_i}\), \(C_k \times C_i\) 个二维卷积核 \({\bm K} \in {\mathbb R}^{C_k \times C_i \times H_k \times W_k}\), 高度与宽度维上填补(padding)大小为 \(H_p×W_p\), 膨胀(dilation)大小为 \(H_d×W_d\), 卷积步长为 \(H_s×W_s\), 在经典膨胀二维卷积神经网络中, 有 \(C_k = C_o, N_o = N_i\), 则卷积后的输出为 \({\bm O} \in {\mathbb R}^{N_o × C_{o}\times H_{o} \times W_{o}}\), 其中

(2.15)\[\begin{array}{ll} H_{o} &= \left\lfloor\frac{H_{i} + 2 \times H_p - H_d \times (H_k - 1) - 1}{H_s} + 1\right\rfloor \\ W_{o} &= \left\lfloor\frac{W_{i} + 2 \times W_p - W_d \times (W_k - 1) - 1}{W_s} + 1\right\rfloor \end{array} \]

对比 式.2.14 和 式.2.15, 可以发现当膨胀大小为 \(H_d×W_d = 1×1\) 时, 膨胀卷积退化为经典卷积.

更多二维卷积示意图参见 A technical report on convolution arithmetic in the context of deep learning.

2.2.2. 经典二维转置卷积运算

二维转置卷积是一种解卷积方法,

设有二维卷积核 \({\bm K} \in {\mathbb R}^{C_o\times H_k \times W_k}\), 二维卷积输入 \({\bm I} \in {\mathbb R}^{N_i × C_{i}\times H_{i} \times W_{i}}\), 高度与宽度维上填补(padding)大小为 \(H_p×W_p\), 膨胀(dilation)大小为 \(H_d×W_d\), 卷积步长为 \(H_s×W_s\), 则卷积后填补(output-padding)大小为 \(H_{op}×W_{op}\), 则卷积后的输出为 \({\bm Y} \in {\mathbb R}^{N × C_{o}\times H_{o} \times W_{o}}\), 其中

(2.16)\[\begin{array}{ll} H_{o} &= (H_{i} - 1) \times H_s - 2 \times H_p + H_d \times (H_k - 1) + H_{op} + 1 \\ W_{o} &= (W_{i} - 1) \times W_s - 2 \times W_p + W_d \times (W_k - 1) + W_{op} + 1 \end{array} \]

2.2.3. 新型卷积

平衡卷积

(2.17)\[{\bm Z}_{n_o, c_i, h_o, w_o} = \sum_{h=0}^{H_k-1}\sum_{w=0}^{W_k-1} \left[{\bm I}_{n_o, c_i, h_o + h - 1, w_o + w - 1} + {\bm K}_{c_o, c_i, h, w} - {\bm I}_{n_o, c_i, h_o + h - 1, w_o + w - 1} \cdot {\bm K}_{c_o, c_i, h, w}\right]. \]

2.2.4. 实验分析

卷积与相关

实验说明

以二维卷积为例, 设有矩阵 \({\bm a}, {\bm b}\),

\[{\bm a} = \left[ {\begin{array}{ccc} 1&2&3\\ 4&5&6\\ 7&8&9 \end{array}} \right] \]
\[{\bm b} = \left[ {\begin{array}{ccc} 1&2\\ 3&4 \end{array}} \right] \]

则有卷积 \({\bm a}*{\bm b}\)

\[{\bm a}*{\bm b} = \left[ {\begin{array}{cccc} 1&4&7&6\\ 7&{23}&{33}&{24}\\ {19}&{53}&{63}&{42}\\ {21}&{52}&{59}&{36} \end{array}} \right] \]

互相关 \({\bm a}\star{\bm b}\)

\[{\bm a}\star{\bm b} = \left[ {\begin{array}{cccc} 4&{11}&{18}&9\\ {18}&{37}&{47}&{21}\\ {36}&{67}&{77}&{33}\\ {14}&{23}&{26}&9 \end{array}} \right] \]

实验结果

在 Matlab 环境中, 输入如下代码, 求解卷积 \({\bm a} * {\bm b}\) 与相关 \({\bm a}\star{\bm b}\)

代码 2.10 2D convolution and cross-correlation Matlab
 0
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
a = [1 2 3;4 5 6;7 8 9];
b = [1 2;3 4];

disp(a)
disp(b)

% convolution
disp(conv2(a, b))

% cross-correlation
disp(xcorr2(a, b))

MATLAB中的2D卷积和相关结果为

 1     2     3
 4     5     6
 7     8     9

 1     2
 3     4

 1     4     7     6
 7    23    33    24
19    53    63    42
21    52    59    36

 4    11    18     9
18    37    47    21
36    67    77    33
14    23    26     9

在 Python 环境中, 输入如下代码, 求解卷积 \({\bm a} * {\bm b}\)

代码 2.11 2D convolution in PyTorch
 0
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
import torch as th

a = th.tensor([[1., 2, 3], [4, 5, 6], [7, 8, 9]])
b = th.tensor([[1., 2], [3, 4]])

a = a.unsqueeze(0)  # 1x3x3
a = a.unsqueeze(0)  # 1x1x3x3
b = b.unsqueeze(0)  # 1x2x2
b = b.unsqueeze(0)  # 1x1x2x2

print(a, a.size())
print(b, b.size())

c = th.conv2d(a, b, stride=1, padding=1)

print(c)

PyTorch中的2D卷积结果为

tensor([[[[1., 2., 3.],
          [4., 5., 6.],
          [7., 8., 9.]]]]) torch.Size([1, 1, 3, 3])
tensor([[[[1., 2.],
          [3., 4.]]]]) torch.Size([1, 1, 2, 2])
tensor([[[[ 4., 11., 18.,  9.],
          [18., 37., 47., 21.],
          [36., 67., 77., 33.],
          [14., 23., 26.,  9.]]]])

注解

对比结果可以发现, PyTorch中的2D卷积实际上是2D相关操作, 与此类似, Tensorflow等深度神经网络框架中的卷积均为相关操作. 但这并不影响网络的性能, 这是因为卷积核是通过网络学习的, 通过学习得到的卷积核可以看作是翻转后卷积核.