2.3. 池化单元¶
2.3.1. 经典二维池化运算¶
与经典二维卷积一样, 池化后的特征图大小为
(2.18)¶\[\begin{array}{ll}
H_{o} &= \left\lfloor\frac{H_{i} + 2 \times P_h - K_h}{S_h} + 1\right\rfloor \\
W_{o} &= \left\lfloor\frac{W_{i} + 2 \times P_w - K_w}{S_w} + 1\right\rfloor
\end{array}
\]
2.3.2. 膨胀二维池化运算¶
(2.19)¶\[\begin{array}{ll}
H_{o} &= \left\lfloor\frac{H_{i} + 2 \times P_h - D_h \times (K_h - 1) - 1}{S_h} + 1\right\rfloor \\
W_{o} &= \left\lfloor\frac{W_{i} + 2 \times P_w - D_w \times (K_w - 1) - 1}{S_w} + 1\right\rfloor
\end{array}
\]
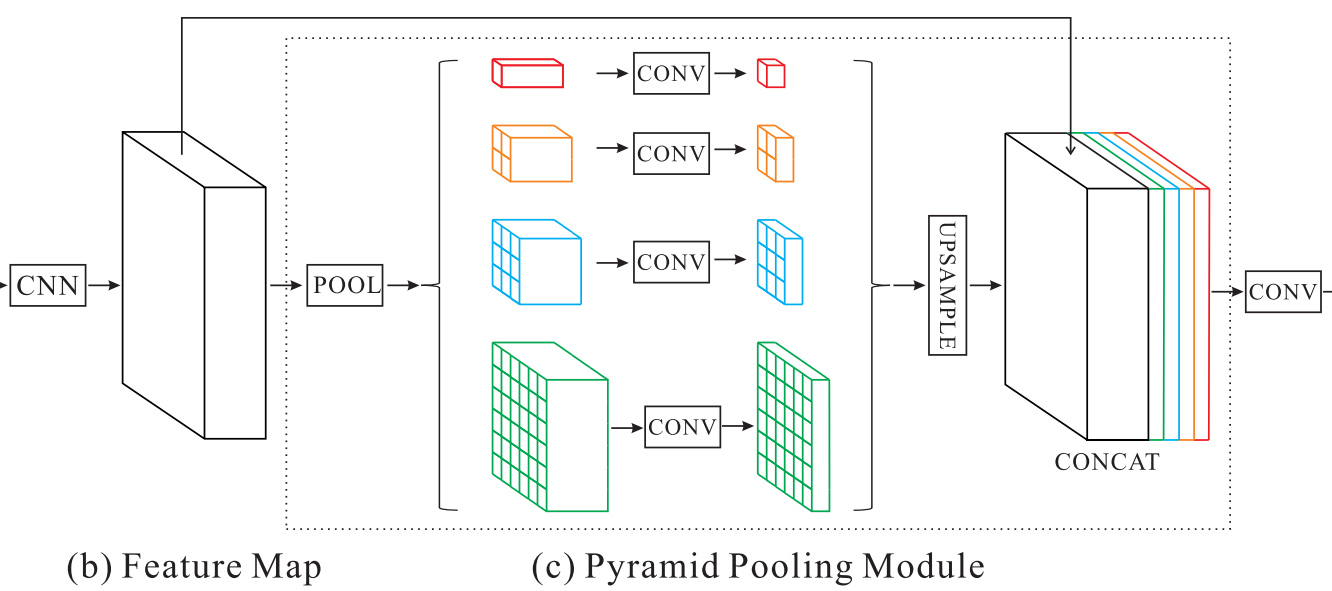
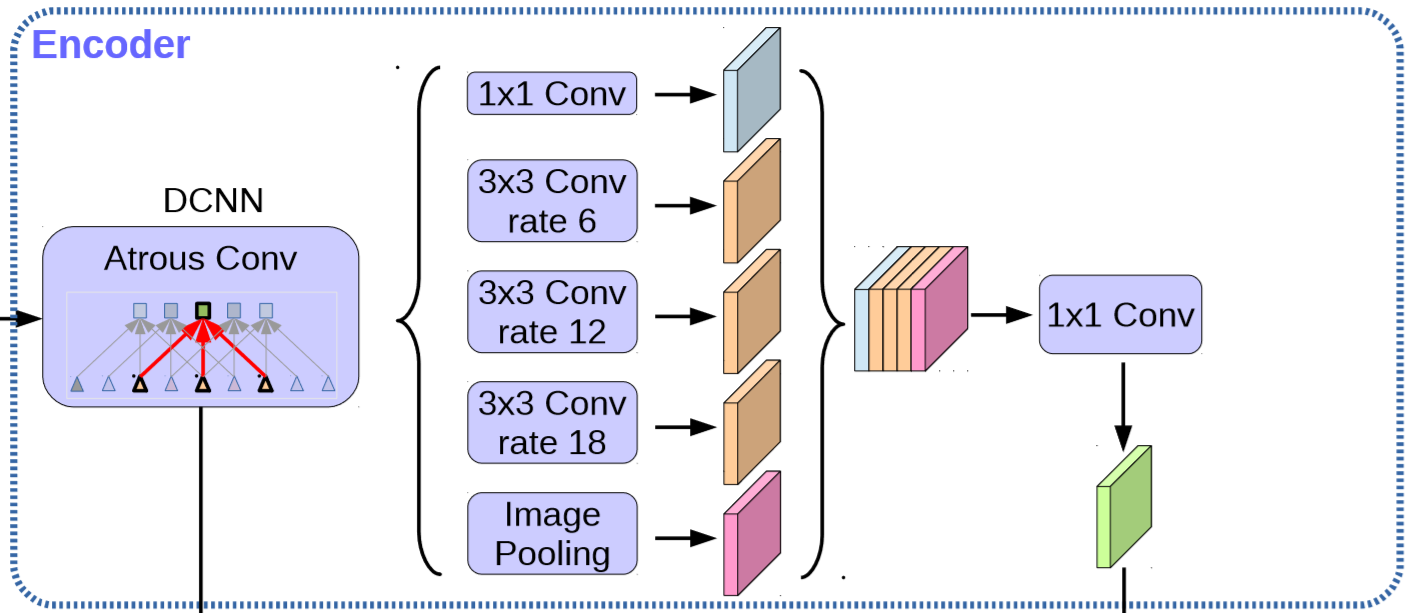
2.3.3. 金字塔池化¶
空间金字塔池化¶
空间金字塔池化(Spatial Pyramid Pooling, SPP)由何凯明等人于2015年提出 [1], 如 图 2.32 所示, 对于任意大小的特征图输出, 通过使用不同池化窗口和步长, 对特征图进行池化, 将特征图划分成具有不同尺度的固定大小特征图, 特征图拉成列向量并连接, 得到固定的输出维度, 实现了多尺度网络的训练以及识别,进而提升了图像分类和目标检测的精度.