2.7. 残差单元

2.7.1. 经典残差块分析

残差块结构

梯度传播分析

利用链式求导法则, 图 2.36 (a) 所示传统神经网络的梯度传播过程可以表示为 式.2.23

(2.23)\[\begin{aligned} \frac{\partial L}{\partial {\bm w}_3} &= \frac{\partial L}{\partial {\bm y}}\times \frac{\partial {\bm y}}{\partial {\bm w}_3}\\ \frac{\partial L}{\partial {\bm w}_2} &= \frac{\partial L}{\partial {\bm y}}\times \frac{\partial {\bm y}}{\partial {\bm h}_3}\times \frac{\partial {\bm h}_3}{\partial {\bm w}_2}\\ \frac{\partial L}{\partial {\bm w}_1} &= \frac{\partial L}{\partial {\bm y}}\times \frac{\partial {\bm y}}{\partial {\bm h}_3}\times \frac{\partial {\bm h}_3}{\partial {\bm h}_2}\times \frac{\partial {\bm h}_2}{\partial {\bm w}_1}\\ \frac{\partial L}{\partial {\bm w}_0} &= \frac{\partial L}{\partial {\bm y}}\times \frac{\partial {\bm y}}{\partial {\bm h}_3}\times \frac{\partial {\bm h}_3}{\partial {\bm h}_2}\times \frac{\partial {\bm h}_2}{\partial {\bm h}_1}\times \frac{\partial {\bm h}_1}{\partial {\bm w}_0}\\ \end{aligned} \]
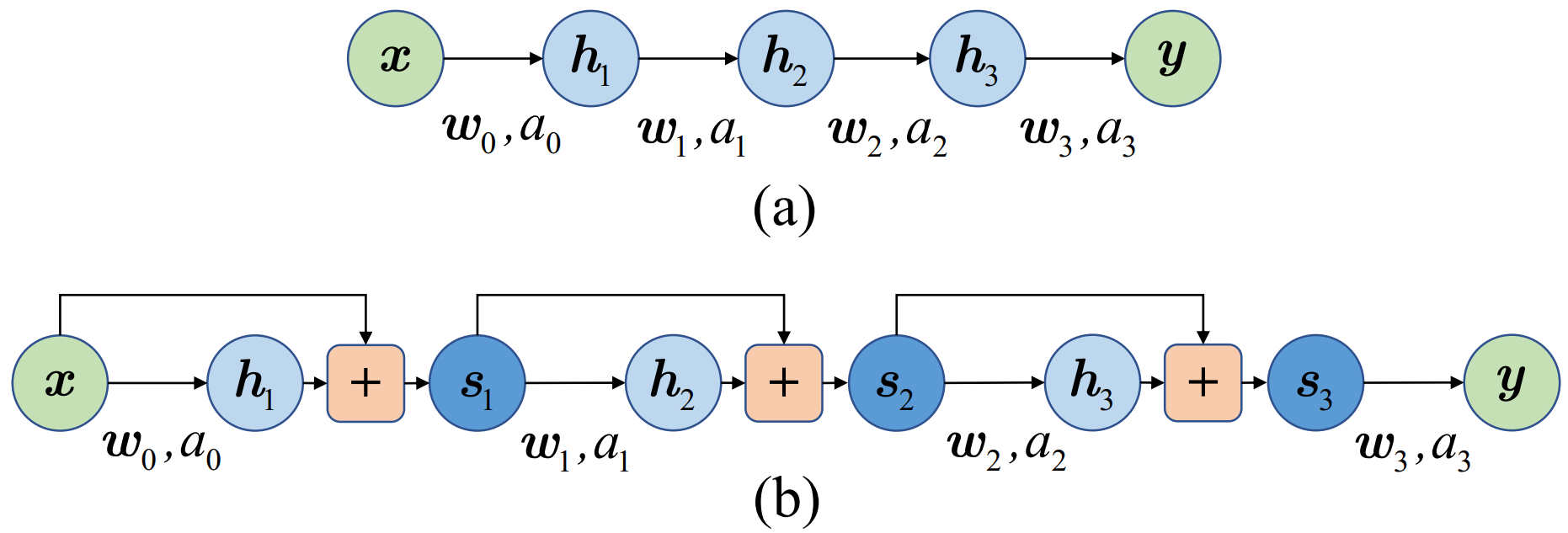
经典神经网络与残差网络结构对比

图 2.36 经典神经网络与残差网络结构对比. (a) 含三个隐藏层的神经网络结构示意图; (b) 含三个残差块的神经网络示意图.

同样地, 根据链式求导法则, 图 2.36 (b) 所示残差神经网络的梯度传播过程可以表示为 式.2.24

(2.24)\[\begin{aligned} \frac{\partial L}{\partial {\bm w}_3} &= \frac{\partial L}{\partial {\bm y}}\times \frac{\partial {\bm y}}{\partial {\bm w}_3}\\ \frac{\partial L}{\partial {\bm w}_2} &= \frac{\partial L}{\partial {\bm y}}\times \frac{\partial {\bm y}}{\partial {\bm s}_3}\times \frac{\partial {\bm s}_3}{\partial {\bm w}_2}\\ \frac{\partial L}{\partial {\bm w}_1} &= \frac{\partial L}{\partial {\bm y}}\times \frac{\partial {\bm y}}{\partial {\bm s}_3}\times \frac{\partial {\bm s}_3}{\partial {\bm s}_2}\times \frac{\partial {\bm s}_2}{\partial {\bm w}_1}\\ \frac{\partial L}{\partial {\bm w}_0} &= \frac{\partial L}{\partial {\bm y}}\times \frac{\partial {\bm y}}{\partial {\bm s}_3}\times \frac{\partial {\bm s}_3}{\partial {\bm s}_2}\times \frac{\partial {\bm s}_2}{\partial {\bm s}_1}\times \frac{\partial {\bm s}_1}{\partial {\bm w}_0}\\ \end{aligned} \]

又 \(\frac{\partial {\bm s}_n}{\partial {\bm w}_{n-1}} = \frac{\partial {\bm h}_n}{\partial {\bm w}_{n-1}}\), \(\frac{\partial {\bm s}_n}{\partial {\bm s}_{n-1}} = \frac{\partial {\bm h}_n}{\partial {\bm s}_{n-1}} + 1\), 代入 式.2.24 中得

(2.25)\[\begin{aligned} \frac{\partial L}{\partial {\bm w}_3} &= \frac{\partial L}{\partial {\bm y}}\times \frac{\partial {\bm y}}{\partial {\bm w}_3}\\ \frac{\partial L}{\partial {\bm w}_2} &= \frac{\partial L}{\partial {\bm y}}\times \frac{\partial {\bm y}}{\partial {\bm s}_3}\times \frac{\partial {\bm h}_3}{\partial {\bm w}_2}\\ \frac{\partial L}{\partial {\bm w}_1} &= \frac{\partial L}{\partial {\bm y}}\times \frac{\partial {\bm y}}{\partial {\bm s}_3}\times \left(\frac{\partial {\bm h}_3}{\partial {\bm s}_2} + 1 \right)\times \frac{\partial {\bm h}_2}{\partial {\bm w}_1}\\ \frac{\partial L}{\partial {\bm w}_0} &= \frac{\partial L}{\partial {\bm y}}\times \frac{\partial {\bm y}}{\partial {\bm s}_3}\times \left(\frac{\partial {\bm h}_3}{\partial {\bm s}_2} + 1 \right)\times \left(\frac{\partial {\bm h}_2}{\partial {\bm s}_1} + 1 \right)\times \frac{\partial {\bm h}_1}{\partial {\bm w}_0}\\ \end{aligned} \]