2.2. 几何法¶
2.2.1. 初始规划¶
2.2.2. 障碍物躲避¶
人工设置多个圆形障碍区域, 要求算法改变初始规划的路线, 使得新规划的路线自动避开障碍区域.
设有待规划区域 \(\mathscr R\), \(N\) 个原始路径有序点集 \({\mathcal P} = \{P_n\}_{n=1}^N\), \(M\) 个障碍圆区域 \({\mathscr O} = \{{\mathcal O}_m\}_{m=1}^M\), 其中, \(P_n=(x_n, y_n)^T\), 障碍物是由方程 \({\mathcal O}_m : (x-x_{c_m})^2 + (y-y_{c_m})^2 \le r_{c_m}\) 确定的圆形区域.
最短圆弧法¶
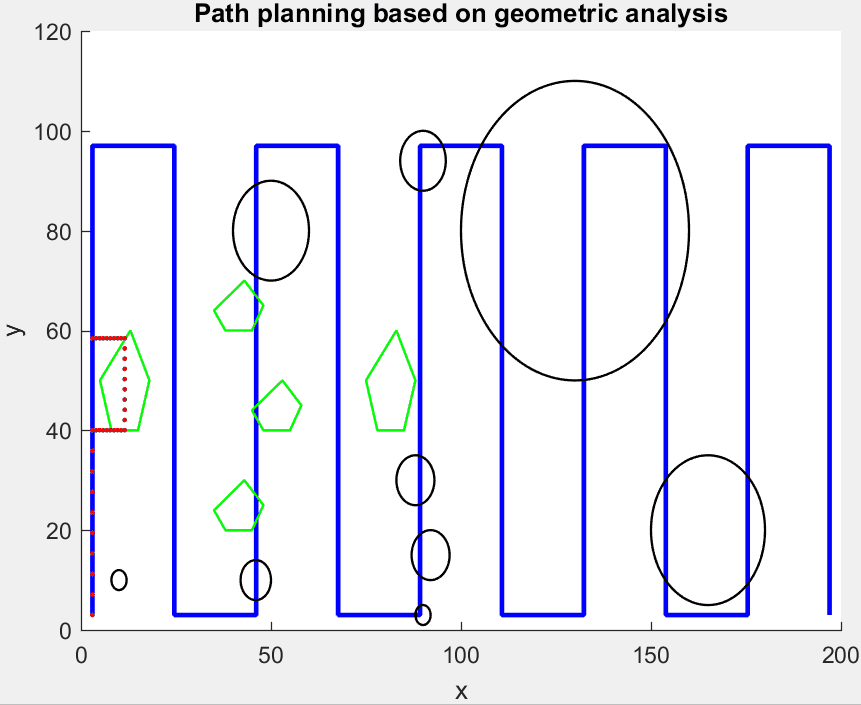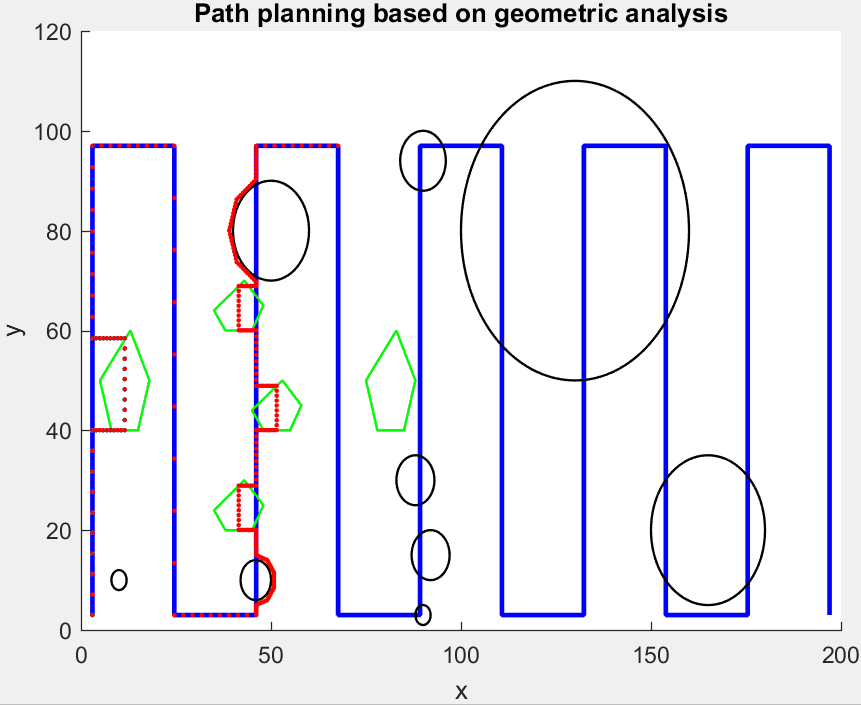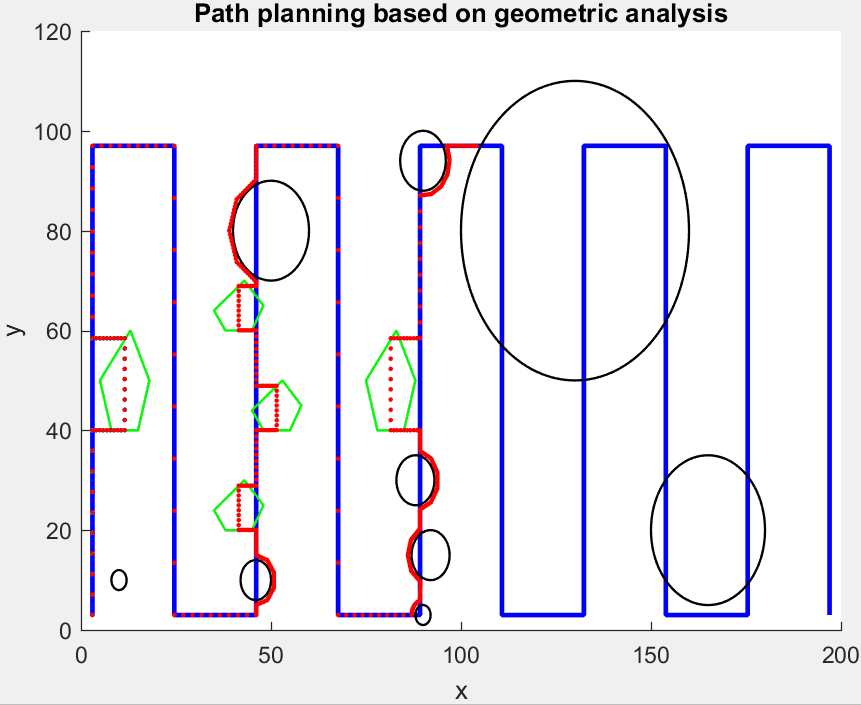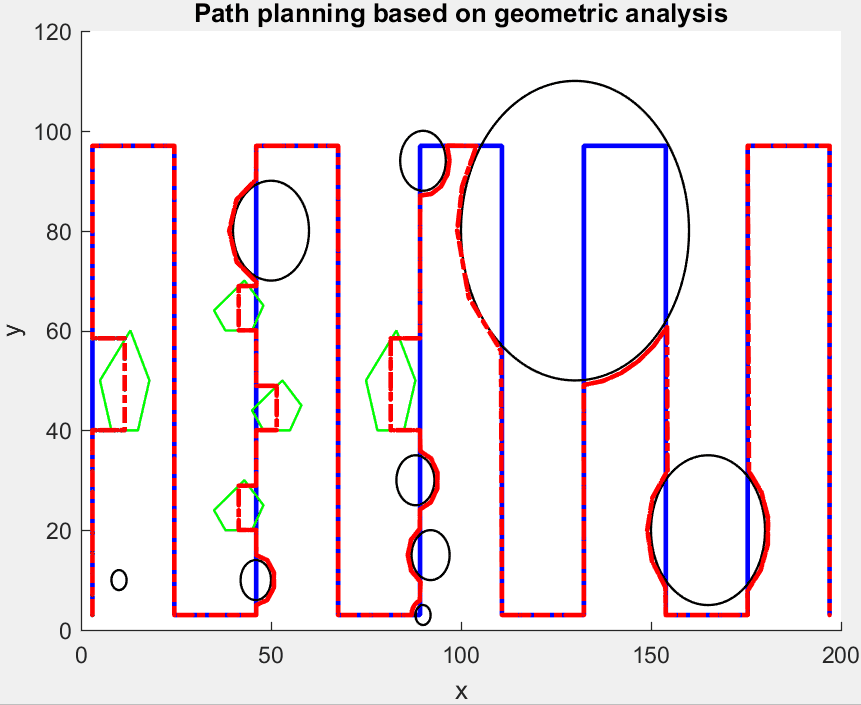
该方法的主要思想是将原始经过障碍圆区域的路径, 转变为与障碍圆圆周相距一安全距离 \(d\) 的一段最短圆弧, 如 图 2.74 所示, 蓝色为原始路径, 黑色圆表示障碍物, 红色圆弧为避障路径. 通过确定连续的两个点, 即入圆点 \(P_a\) 和出圆点 \(P_b\), 对圆弧 \(\overset{\frown}{P_aP_b}\) 进行离散化得到重新规划的避障路径.
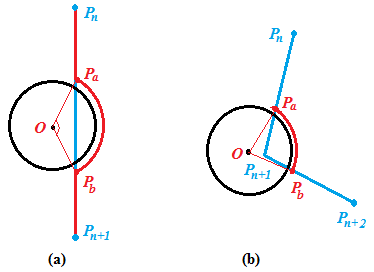
图 2.74 圆形障碍物躲避示意图¶
详细的算法步骤陈述如下
注解
最短圆弧法避障算法
输入: 原始路径有序点集构成的矩阵 \({\bm P} = [x_1, y_1\; x_2, y_2\; \cdots\; x_N, y_N] \in {\mathbb R}^{N\times 2}\), \(M\) 个障碍圆区域参数构成的矩阵 \({\bm C} = [x_{c_1}, y_{c_1}, r_{c_1}\; x_{c_2}, y_{c_2}, r_{c_2}\; \cdots\; x_{c_M}, y_{c_M}, r_{c_M}] \in {\mathbb R}^{N\times 3}\), 安全距离 \(d\), 角度采样点数 \(N_{\theta}\).
输出: 规划后的路径有序点集构成的矩阵 \({\bm R}\)
Step0: 初始化规划路径 \({\bm R} = {\bm P}\), 圆心 \({\bm O}={\bm C}(N, 1:2)\)
Step1: 计算每一个障碍圆圆心 \({\bm O}\) 到原始路径中每一条线段(共 \(N-1\), 并找出距离小于 \(r\) 的线段, 记为 \({\mathcal L}\in {\mathbb R}^{L\times 4}\).
Step2: 对这些线段进行离散化, 并判断离散化的点是否在圆内, 从而得到若干入圆点出圆点对 \(\{P_a,P_b\}\)
Step3: 对每一个入圆点出圆点对 \(P_a,P_b\), 计算夹角 \(\theta_a = <\vec{OP_a}, \vec{{\bm e}_x}>\), \(\theta_b = <\vec{OP_b}, \vec{{\bm e}_x}>\), 其中, \({\bm e}_x = [1 ,0]^T\)
Step4: 若 \(|\theta_b - \theta_a| < \pi\), 则离散化角度区间 \(\theta=[\theta_a, \theta_b]_{N_{\theta}}\); 否则离散化角度区间 \(\theta=[[\theta_a, π\theta_a/|\theta_a|]_{N_{\theta}/2}, [π\theta_b/|\theta_b|, \theta_b]_{N_{\theta}/2}]\)
Step5: 生成圆心为 \({\bm O}\), 半径为 \({\bm r}+d\), 一段圆弧 \(\overset{\frown}{P_aP_b}\), 并插入到路径有序点集中 \(\bm R\) 中.
Step6: 输出 \(\bm R\).
2.2.3. 价值区域穿越¶
人工设置多个凸多边形高价值区域, 要求算法根据设置的区域, 改变初始规划的路线, 使得新规划的路线经过高价值区域.
设有待规划区域 \(\mathscr R\), \(N\) 个原始路径有序点集 \({\mathcal P} = \{P_n\}_{n=1}^N\), \(M\) 个高价值区域 \({\mathscr V} = \{{\mathcal V}_m\}_{m=1}^M\), 其中, \(P_n=(x_n, y_n)^T\), 价值区域是由有序点集 \({\mathcal V}_m : \{(x_1^{v_m}, y_1^{v_m}), (x_2^{v_m}, y_2^{v_m}), \cdots (x_K^{v_m}, y_K^{v_m})\}\) 围成的多边形区域.
矩形插入法¶
算法描述: 对于每一个价值区域, 计算重心, 找到原始路径线段中与重心相距最近的线段 \(L_s=\vec{P_0 P_1}\), 接着计算过重心且与该线段 \(L_s\) 平行的线与凸多边形区域的交点 \(Q_1,Q_2\), 分别计算点 \(Q_1, Q_2\) 在线段 \(L_s\) 上的垂直投影点, 记为 \(U_1, U_2\), 若 \(||P_0-U_1||_2^2 \le ||P_0-U_2||_2^2\), 则更新路径为 \(U_1→Q_1→Q_2→U_2\), 反之则更新路径为 \(U_2→Q_2→Q_1→U_1\).
2.2.4. 实验与分析¶
实验1¶
实验代码¶
具体代码可以在作者GitHub仓库获取, 地址为 mpathplanning.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 | clc
clear all
close all
safedist = 1;
NA = 6;
dedge = 3;
dsep = 20;
PlanningRegion = [0 0; 200 0; 200 100; 0 100];
ValueRegions = {
[10 40; 15 40; 18 50; 13 60; 5 50; 8 40]
[40 20; 45 20; 48 25; 43 30; 35 24; 38 20]
[50 40; 55 40; 58 45; 53 50; 45 44; 48 40]
[40 60; 45 60; 48 65; 43 70; 35 64; 38 60]
[80 40; 85 40; 88 50; 83 60; 75 50; 78 40]
};
ObstacleRegions = [
10, 10, 2;
46, 10, 4;
50, 80, 10;
88, 30, 5;
92, 15, 5;
90, 3, 2;
90, 94, 6;
165, 50, 5;
];
%% Generates Original Path
xmin = min(PlanningRegion(:, 1));
xmax = max(PlanningRegion(:, 1));
ymin = min(PlanningRegion(:, 2));
ymax = max(PlanningRegion(:, 2));
Nx = uint16(((xmax-dedge) - (xmin+dedge)) / dsep);
x1 = linspace(xmin+dedge, xmax-dedge, Nx)';
x2 = linspace(xmin+dedge, xmax-dedge, Nx)';
y1 = ones(Nx, 1) * (ymin + dedge);
y2 = ones(Nx, 1) * (ymax - dedge);
xy1 = [x1 y1];
xy2 = [x2 y2];
OriginalPath = zeros(2*Nx, 2);
idx = 1:2:Nx;
OriginalPath(idx*2-1, :) = xy1(idx, :);
idx = 2:2:Nx;
OriginalPath(idx*2, :) = xy1(idx, :);
idx = 1:2:Nx;
OriginalPath(idx*2, :) = xy2(idx, :);
idx = 2:2:Nx;
OriginalPath(idx*2-1, :) = xy2(idx, :);
figure
title('Path planning based on geometric analysis')
xlabel('x')
ylabel('y')
hold on
% origional path
opplot(OriginalPath, '-b', 'linewidth', 1);
ReplanedPath = OriginalPath;
%% Valuable Regions Path Planning
% show polygonal valuable regions
cpplot(ValueRegions, '-g', 'linewidth', 1)
% polygonal valuable region passing program based on geometric method
ReplanedPath = pvp_geometry(ReplanedPath, ValueRegions);
%% Obstacle Path Planning
% show cicular obstacles
circleplot(ObstacleRegions, '-k', 'linewidth', 1)
% cicular obstacle avoidance program based on geometric method
ReplanedPath = coa_geometry(ReplanedPath, ObstacleRegions, safedist, NA);
% smooth
% P = smooth_path(P);
% display planning path dynamically, 0.3s/point
dynshow(ReplanedPath, 0.3, 10, '.r', 'linewidth', 2);
% show final planning path
opplot(ReplanedPath, '-m', 'linewidth', 2);
|