1.3. 相似性度量指标¶
1.3.1. 集合方法¶
Jaccard¶
Jaccard 指数与距离¶
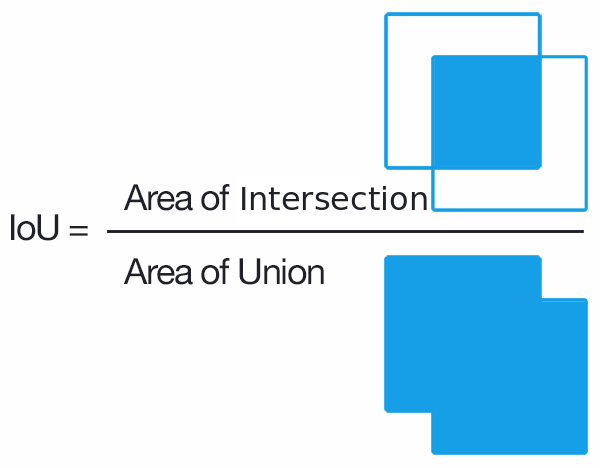
Jaccard 指数 (index), 也称为并上交 (Intersection over Union, IoU) 或 Jaccard 相似性系数 (Jaccard Similarity Coefficient), 用于测量样本集的相似性与多样性. Jaccard系数用于衡量有限样本集间的相似性, 被定义为集合交的势除并的势.
(1.32)¶\[J({\mathbb A}, {\mathbb B})=\frac{|{\mathbb A} \cap {\mathbb B}|}{|{\mathbb A} \cup {\mathbb B}|}=\frac{|{\mathbb A} \cap {\mathbb B}|}{|{\mathbb A}|+|{\mathbb B}|-|{\mathbb A} \cap {\mathbb B}|}
\]
其中, \(|\mathbb A|\) 表示集合 \(\mathbb A\) 的势 1, \(0 < J({\mathbb A}, {\mathbb B}) < 1\), 若 \({\mathbb A}, {\mathbb B}\) 为空集, 定义 \(J({\mathbb A}, {\mathbb B}) = 1\).
Jaccard 距离用于衡量样本集合间的差异, 常定义如下:
\[d_{J}({\mathbb A}, {\mathbb B})=1-J({\mathbb A}, {\mathbb B})=\frac{|{\mathbb A} \cup {\mathbb B}|-|{\mathbb A} \cap {\mathbb B}|}{|{\mathbb A} \cup {\mathbb B}|}
\]
加权 Jaccard 指数与距离¶
概率 Jaccard 指数与距离¶
Dice 系数¶
Sørensen–Dice coefficient 简称为 Dice Coefficient 或 Dice Similarity Coefficient, 衡量两个样本集合的相似性, 给定集合 \({\mathbb A}, {\mathbb B}\), Dice系数定义为
(1.35)¶\[S = {\rm DSC} = \frac{2|{\mathbb A}\cap{\mathbb B}|}{|{\mathbb A}|+|{\mathbb B}|}.
\]
对于二值数据, 采用 true positive (TP), false positive (FP), 和 false negative (FN) 的定义, 则Dice系数可以表示为
(1.34)¶\[S = {\rm DSC} = \frac{2{\rm TP}}{2{\rm TP} + {\rm FP} + {\rm FN}}.
\]
容易得出 Dice系数与Jaccard系数间存在如下关系
(1.35)¶\[\begin{array}{l}{J=S /(2-S)} \\ {S=2 J /(1+J)}\end{array}.
\]
且此时有 \({\rm DSC} = {\rm F}_1\).
提示
将查准率 式.1.27 与查全率 式.1.28 代入 式.1.27 中, 有
\[F_1 = \frac{(1+1^2)⋅P⋅R}{1^2⋅P+R} = \frac{(1+1^2)⋅\frac{\rm TP}{{\rm TP} + {\rm FP}}⋅ \frac{\rm TP}{{\rm TP} + {\rm FN}}}{1^2⋅\frac{\rm TP}{{\rm TP} + {\rm FP}} + \frac{\rm TP}{{\rm TP} + {\rm FN}}}\\
=\frac{2{\rm TP}^2}{({\rm TP}+{\rm FP})({\rm TP}+{\rm FN})}⋅\frac{({\rm TP}+{\rm FP})({\rm TP}+{\rm FN})}{{\rm TP}(2{\rm TP}+{\rm FP}+{\rm FN})}\\
= \frac{2{\rm TP}}{2{\rm TP} + {\rm FP}+ {\rm FN}} = {\rm DSC}
\]