4.2.3. 小波变换¶

小波与小波变换¶

小波及其性质¶

小波 ( Wavelet ) , 即小区域的波, 是一种特殊的, 长度有限的, 平均值为零的波形.

特点:

“小”: 在时域具有紧支集或近似紧支集
“波”: 正负交替的”波动性” , 直流分量为零
信号可分解为一系列由同一母小波函数经平移与尺度伸缩得到的小波函数的叠加

将小波母函数 \(\psi(t)\) 进行平移与尺度伸缩, 得到

\[\psi_{a, \tau}(t) = \frac{1}{\sqrt a}\psi\left(\frac{t-\tau}{a}\right) , a, \tau \in {\mathbb R}, a > 0 \]

由同一小波母函数 \(\psi(t)\) 进行平移与尺度伸缩后得到的一组函数序列称为 小波函数基 .

小波变换¶

小波 ( Wavelet ) 是一种数学函数, 用来将给定的函数或连续时间信号分解成不同的尺度分量. 通常人们可以为每个尺度分量指定一个频率范围. 小波变换 是指用小波表示一个函数. 小波是有限长度或快速衰减振荡波 (称为母小波 Mother Wavelet ) 的缩放和平移后的波 (称为子小波 Daughter Wavelet ). 与传统的傅立叶变换相比, 小波变换在表示具有不连续性和尖峰的函数以及精确解构和重构有限长, 非周期或非平稳信号方面具有优势.

小波变换分为离散小波变换和连续小波变换. 注意, 离散小波变换和连续小波变换都是连续时间 (模拟) 变换. 它们可以用来表示连续时间 (模拟) 信号. 连续小波变换在所有可能的尺度和平移上执行, 而离散小波变换使用尺度与平移参数的特定的量化后的子集.

尺度与频率的关系¶

设 \(a\) 为尺度, \(F_s\) 为采样频率, \(F_c\) 为小波中心频率, 则 \(a\) 对应的实际频率 \(F_a = \frac{F_cF_s}{a}\) .

连续小波变换¶

连续小波变换 ( Continuous Wavelet Transform, CWT) 提供了对信号的过完备表示, 通过取各种平移 (translation) 与缩放 (scale) 参数得到一组小波函数基.

函数 \(x(t)\) 在尺度因子 \(a, a>0, a\in {\mathbb R}\) , 平移因子 \(\tau\) 下的连续小波变换表示为

\[{\rm{CWT}}\{x(t)\}(a, \tau) = X(a, \tau) = \left\langle {x(t),\;{\psi _{a,\tau }}(t)} \right\rangle = \frac{1}{\sqrt{a}} \int_{-\infty}^{+\infty} x(t) \overline{\psi}\left(\frac{t-\tau}{a}\right) {\rm d}t \]

其中, \(\psi\) 为时域与频域的连续函数, 即小波母函数, \(\overline{\psi}\) 表示复共轭.

连续小波种类¶

Continuous wavelets
- Real-valued
  
  Beta wavelet
  
  Hermitian wavelet
  
  Hermitian hat wavelet
  
  Meyer wavelet
  
  Mexican hat wavelet
  
  Poisson wavelet
  
  Shannon wavelet
  
  Spline wavelet
  
  Stromberg wavelet
- Complex-valued
  
  Complex Mexican hat wavelet
  
  fbsp wavelet
  
  Morlet wavelet
  
  Shannon wavelet
  
  Modified Morlet wavelet

Mexh小波¶

Mexican Hat小波函数为 Gauss 函数的二阶导数, 即

\[\psi(t) = (1-t^2)e^{-\frac{t^2}{2}} \]

\[\psi(\omega) = \sqrt{2\pi}\omega^2e^{-\frac{\omega^2}{2}} \]

Morlet小波¶

Morlet小波为 Gauss 包络下的单频复正弦函数, 即

\[\psi(t) = Ce^{-\frac{t^2}{2}} {\rm{cos}}(5t) \]

算法步骤¶

Step1: 选择小波函数及其尺度值 \(a\)
Step2: 从信号起始位置开始, 将小波函数与信号进行比较, 计算小波系数
Step3: 沿时间轴移动小波函数, 即改变平移参数 \(\tau\) , 在新的位置计算小波系数, 直至信号终点
Step4: 改变尺度参数 \(a\) 的值, 重复 Step2, Step3

离散小波变换¶

离散小波变换 ( Discrete Wavelet Transform, DWT) 提供了对信号的过完备表示.

离散小波种类¶

Discrete wavelets
- Beylkin
- BNC wavelets
- Coiflet
- Cohen-Daubechies-Feauveau wavelet (Sometimes referred to as CDF N/P or Daubechies biorthogonal wavelets)
- Daubechies wavelet
- Binomial-QMF (Also referred to as Daubechies wavelet)
- Haar wavelet
- Mathieu wavelet
- Legendre wavelet
- Villasenor wavelet
- Symlet

Haar小波¶

Haar小波函数为:

\[\psi (t) = \left\{ {\begin{array}{ccc} {1,\;\;\;\;\;0 \le t \le 1/2}\\ { - 1,\;\;\;1/2 \le t \le 1}\\ {0,\;\;\;{\rm{otherwise}}} \end{array}} \right. \]

连续逆小波变换¶

设有连续时间信号 \(x(t)\) 的CWT变换表示 \(X(a, \tau)\) , 则

\[x(t) = \frac{1}{2\pi \overline{\hat{\psi}}}(1)\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty} \frac{1}{a^2} X(a, \tau)e^{j\frac{t-\tau}{a}} {\rm d}\tau {\rm d}a \]

其中, \(\hat{\psi}\) 表示 \(\psi\) 的傅里叶变换.

由逆变换知小波函数应定义为

\[\psi(t) = w(t)e^{jt} \]

其中, \(w(t)\) 是窗函数, 这种定义的小波称为分析小波, 因为它可以进行时频分析, 分析小波是不需要满足容许条件的.

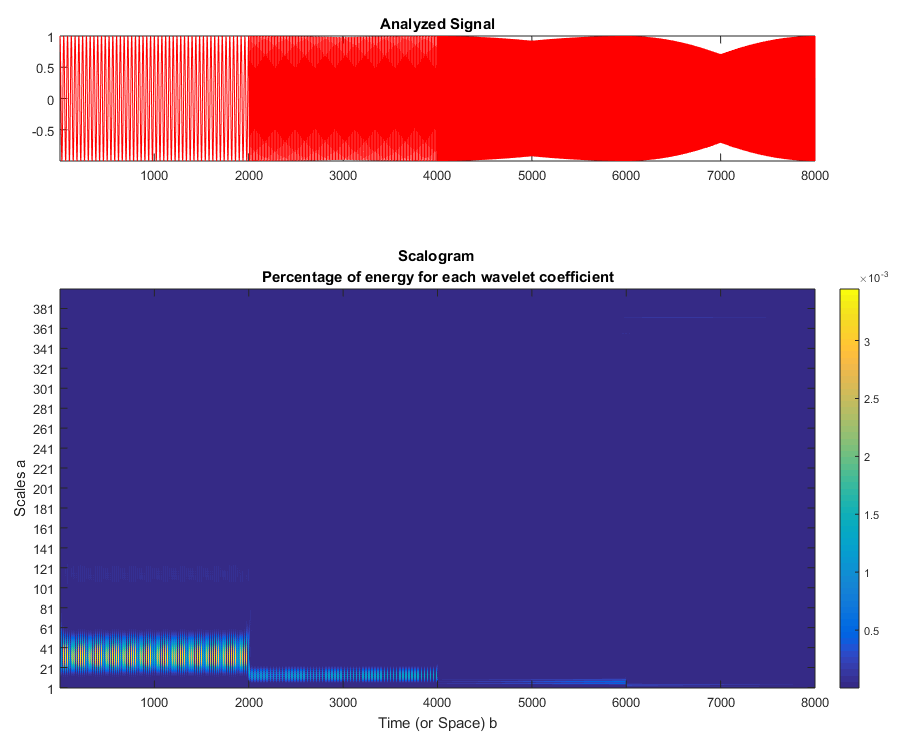
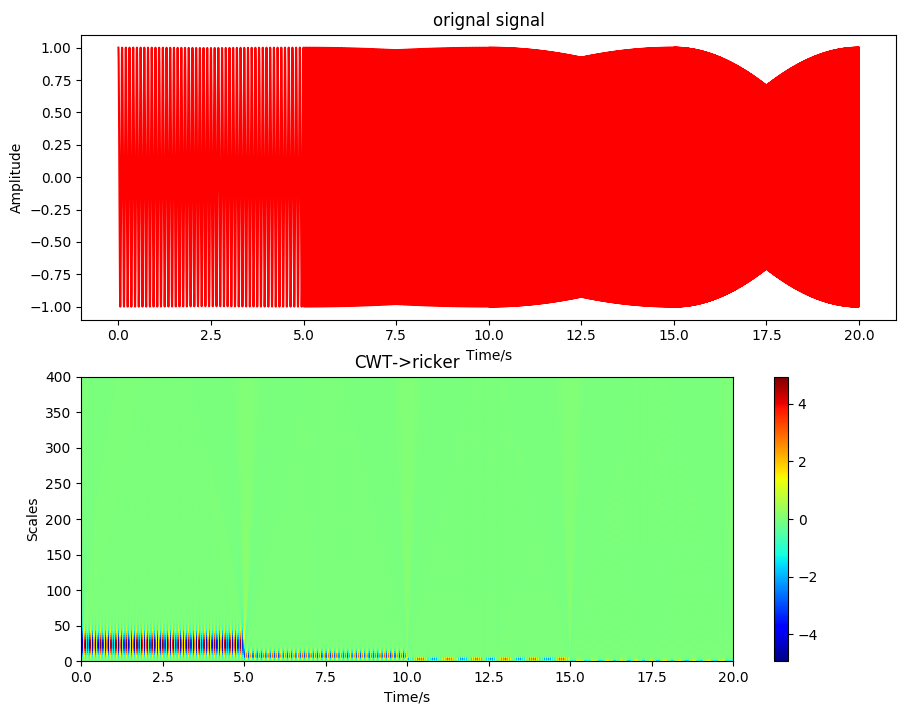
实例分析¶

仿真信号¶

实验内容¶

生成四个子信号, 四种频率:

\[x_1 = {\rm cos}(2πf_1 t), (0\Delta T \leq t < 1\Delta T) \\ x_2 = {\rm cos}(2πf_2 t), (1\Delta T \leq t < 2\Delta T) \\ x_3 = {\rm cos}(2πf_3 t), (2\Delta T \leq t < 3\Delta T) \\ x_4 = {\rm cos}(2πf_4 t), (3\Delta T \leq t < 4\Delta T) \\ \]

合成一个信号, 含上述四种频率:

\[x = x_1 + x_2 + x_3 + x_4 \]

做CWT分析

实验代码¶

MATLAB代码:

PYTHON代码:

实验结果¶

图 4.18 MATLAB CWT结果¶

使用MATLAB对合成的信号进行CWT分析.

图 4.19 PYTHON CWT结果¶

使用PYTHON对合成的信号进行CWT分析.