4.2.2. 短时傅立叶变换

短时傅立叶变换

短时傅立叶变换 ( Short Time Fourier Transform , STFT) 是和傅里叶变换相关的一种数学变换, 用以确定时变信号其局部区域正弦波的频率与相位. 通过将长时间信号分成等长的短的片段, 计算每个片段的傅里叶变换, 将这些片段组成一个频率-时间矩阵得到. 与傅里叶变换类似, 分为连续时间 (Continuous-time) STFT 和离散时间 (Discrete-time) STFT.

连续时间STFT

设有连续时间信号 \(x(t)\) , 窗函数 \(w(t)\) , 在信号上滑动窗函数, 计算信号与窗函数乘积的傅里叶变换, 得到连续时间信号的二维时频STFT表示, 即

\[{\rm STFT}\{x(t)\}(\tau, \omega) = X(\tau, \omega) = \int_{-\infty}^{+\infty}x(t)w(t-\tau)e^{-j\omega t}{\rm d}t \]

其中, \(t, \tau\) , \(\omega=2\pi f\) 均为连续的.

提示

信号 \(x(t)\) 的傅里叶变换表示为

\[F(\omega) = \int_{-\infty}^{+\infty} x(t)e^{-j\omega t} {\rm d}t \]

逆傅里叶变换表示为

\[x(t) = \frac{1}{2\pi}\int_{-\infty}^{+\infty}F(\omega)e^{+j\omega t} {\rm d}\omega \]

离散时间STFT

设有离散时间信号 \(x[n]\) , 窗函数 \(w[n]\) , 在信号上滑动窗函数, 计算信号与窗函数乘积的傅里叶变换, 得到离散时间信号的二维时频STFT表示, 即

\[{\rm STFT}\{x[n]\}(m, \omega) = X(m, \omega) = \sum_{n=-\infty}^{+\infty} x[n]w[n-m]e^{-j\omega n} \]

其中, \(n, m\) 是离散的, \(\omega=2\pi f\) 为连续的. 然而, 通常情况下傅里叶变换采用快速傅里叶变换(FFT)计算, 此时 \(\omega\) 也是离散的.

提示

通常情况下, 窗取为重叠的 (overlap) ,

频谱表示

信号的功率谱密度的频谱表示为STFT结果的平方

\[{\rm{spectrogram}}\{x(t)\}(\tau, \omega) = |X(\tau, \omega)|^2 \]

逆短时傅立叶变换

STFT是可逆的, 即原始信号可以从变换后的数据中恢复出来.

连续时间逆STFT

设有连续时间信号 \(x(t)\) 的STFT表示 \(X(\tau, \omega)\) , 则

\[x(t) = \frac{1}{2\pi}{\int_{-\infty}^{+\infty}}{\int_{-\infty}^{+\infty}} X(\tau, \omega)e^{+j\omega t} {\rm d}\tau {\rm d}\omega \]

或

\[x(t) = {\int_{-\infty}^{+\infty}}\left[\frac{1}{2\pi}{\int_{-\infty}^{+\infty}} X(\tau, \omega)e^{+j\omega t} {\rm d}\omega\right]{\rm d}\tau \]

离散时间逆STFT

实现步骤

• 离散时间STFT

  • 使用窗函数在信号上滑动, 将长时间信号分成等长的短的片段

  • 计算每个片段与窗函数乘积的傅里叶变换

  • 计算每个片段变换后的幅度或功率密度谱

  • 将这些片段组成一个频率-时间矩阵

实例分析

实验1: 仿真信号

实验内容

生成四个子信号, 四种频率:

\[x_1 = {\rm cos}(2πf_1 t), (0\Delta T \leq t < 1\Delta T) \\ x_2 = {\rm cos}(2πf_2 t), (1\Delta T \leq t < 2\Delta T) \\ x_3 = {\rm cos}(2πf_3 t), (2\Delta T \leq t < 3\Delta T) \\ x_4 = {\rm cos}(2πf_4 t), (3\Delta T \leq t < 4\Delta T) \\ \]

合成一个信号, 含上述四种频率:

\[x = x_1 + x_2 + x_3 + x_4 \]

做以下实验

1. 不同窗

2. Gauss窗, 不同std

3. Gauss窗, 不同窗大小

4. Gauss窗, 不同重叠大小

5. Gauss窗, 不同FFT大小

实验代码

核心函数: scipy.signal.spectral.spectrogram

1. 不同窗: demo_stft_windows.py

2. 不同窗, 不同窗大小: demo_stft_gauss_windowsize.py

3. Gauss窗, 不同std: demo_stft_gauss_std.py

4. Gauss窗, 不同窗大小: demo_stft_gauss_windowsize.py

5. Gauss窗, 不同重叠大小: demo_stft_gauss_noverlap.py

6. Gauss窗, 不同FFT大小: demo_stft_gauss_nfft.py

实验结果

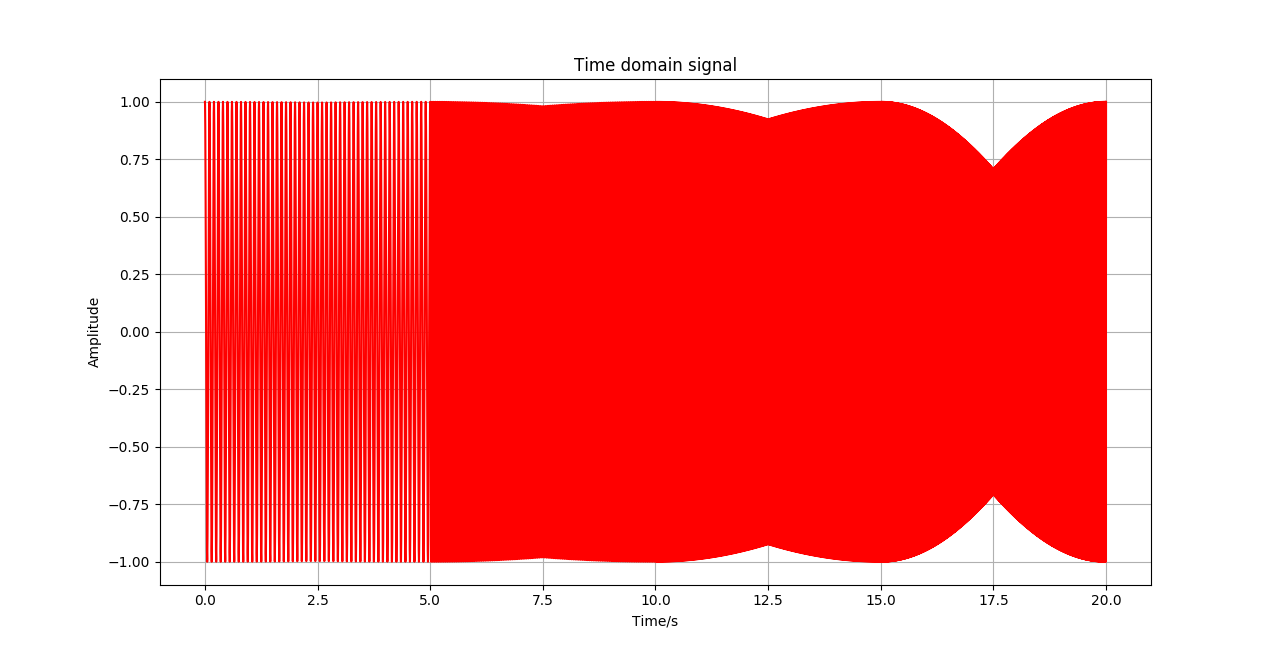
实验中, 设四种信号频率为: \(f_1=10Hz, f_2=25Hz, f_3=50Hz, f_4=100Hz\) , \(\Delta T = 5s\) , 采样率为 \(400Hz\) , 共 \(8000\) 个样本点, 生成的合成信号如下图

图 4.9 Synthetic signal

合成的信号, 包含四种频率成分.

1. 不同窗

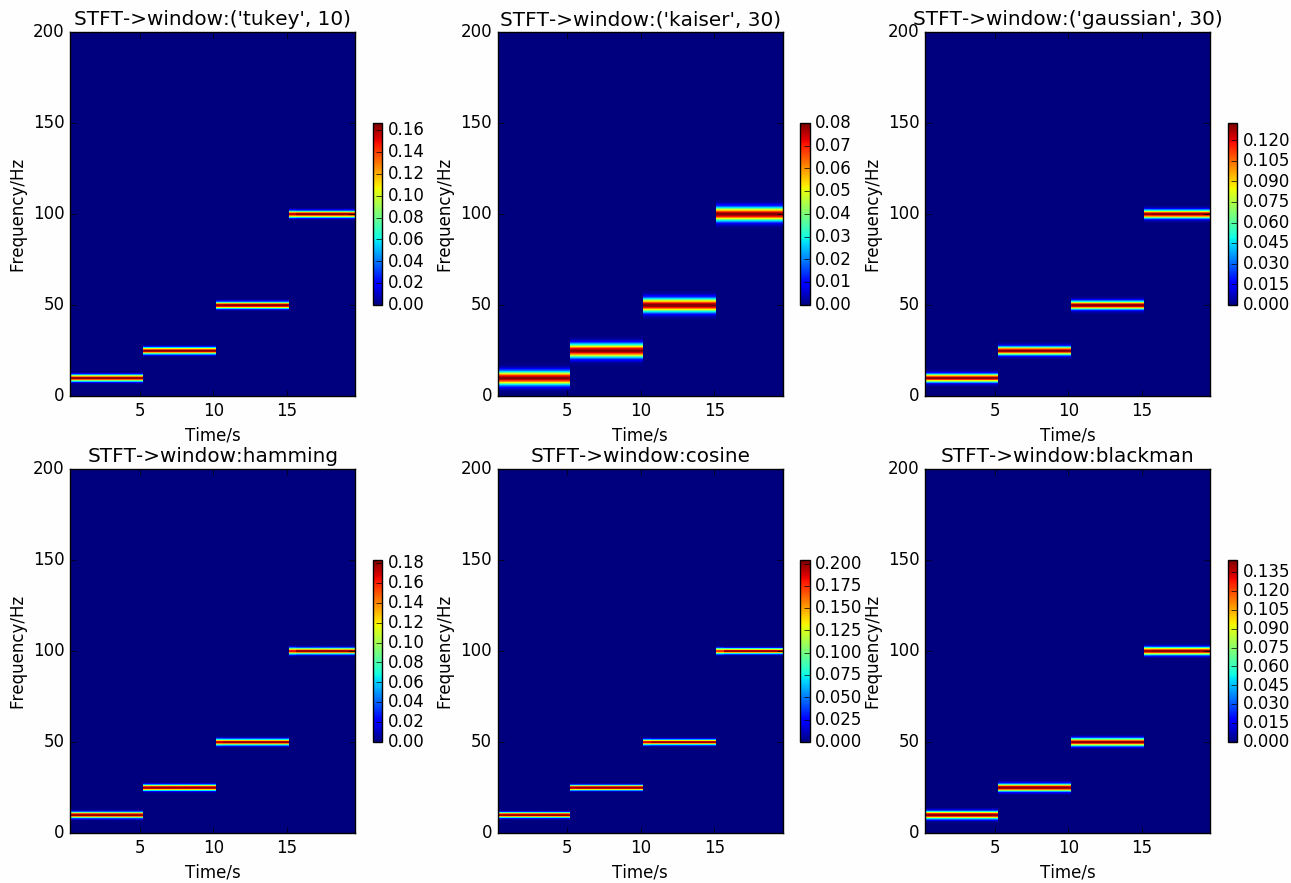
图 4.10 STFT在不同窗下的结果

对合成信号施加六种不同的窗 ( tukey, kaiser, gauss, hamming, cosine, blackman), 窗大小取 \(500ms\) , FFT点数取 \(2048\), 重叠点数取 \(1\) , 然后进行STFT分析.

2. 不同窗, 不同窗大小

对合成信号施加不同窗, 并改变窗大小, FFT点数取 \(2048\) , 重叠点数取 \(1\) , 其它参数见图. 由图可见窗大小影响较大, 窗过小, 频率难分辨.

窗大小为 \(10ms\) 时的结果

图 4.11 STFT在窗大小为 \(10ms\) 时的结果

窗大小为 \(100ms\) 时的结果

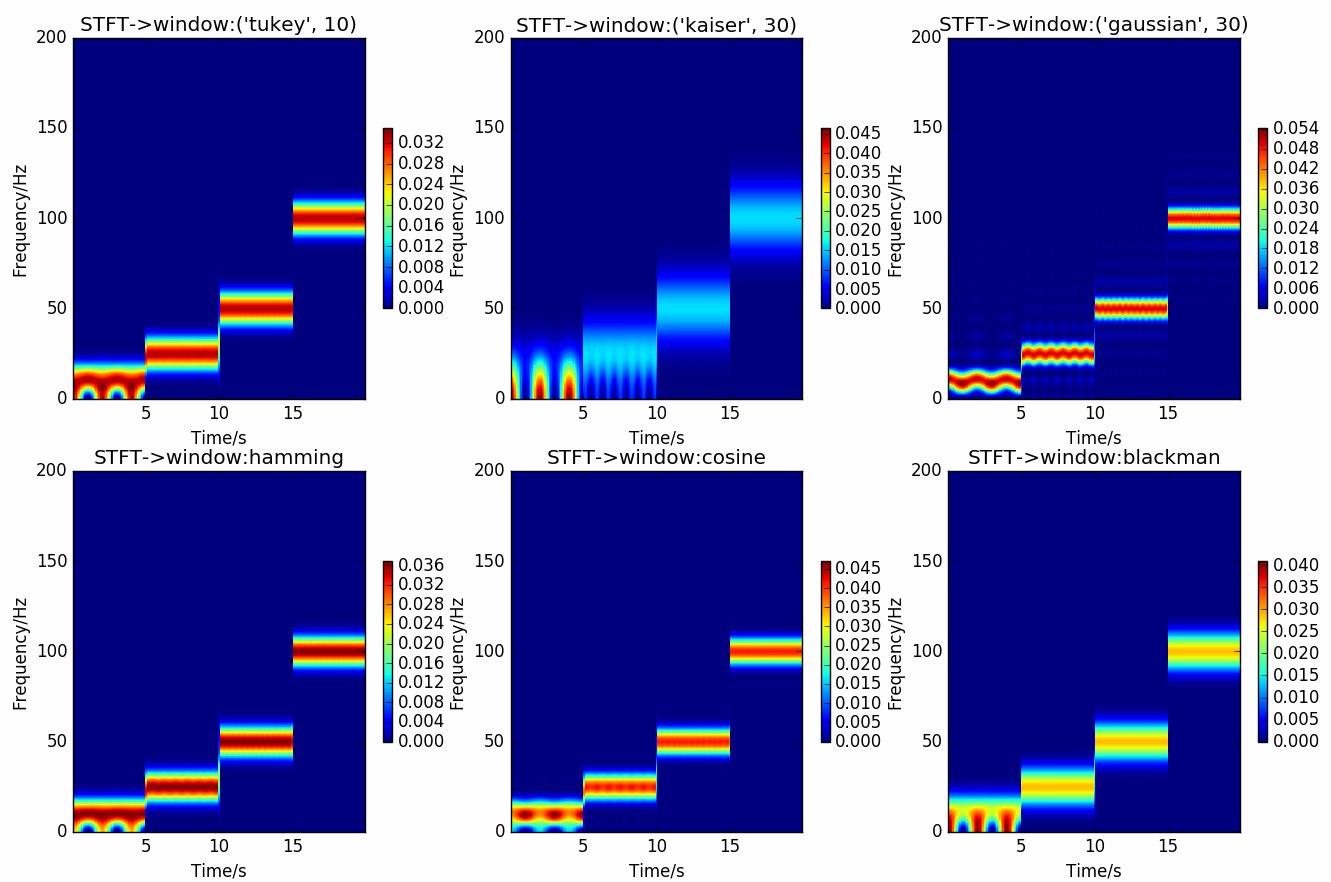
图 4.12 STFT在窗大小为 \(100ms\) 时的结果

窗大小为 \(1000ms\) 时的结果

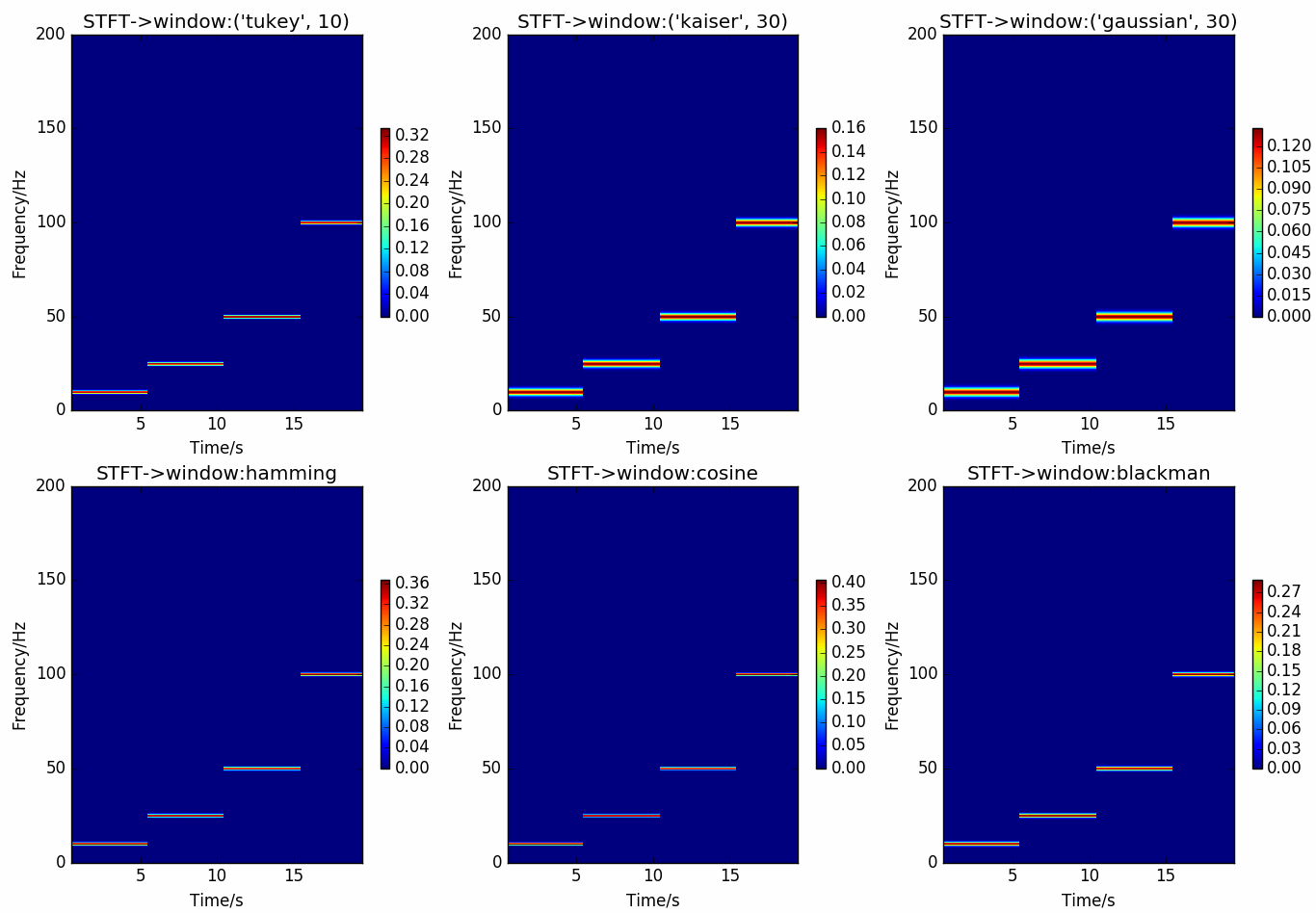
图 4.13 STFT在窗大小为 \(1000ms\) 时的结果

3. gauss窗, 不同 std

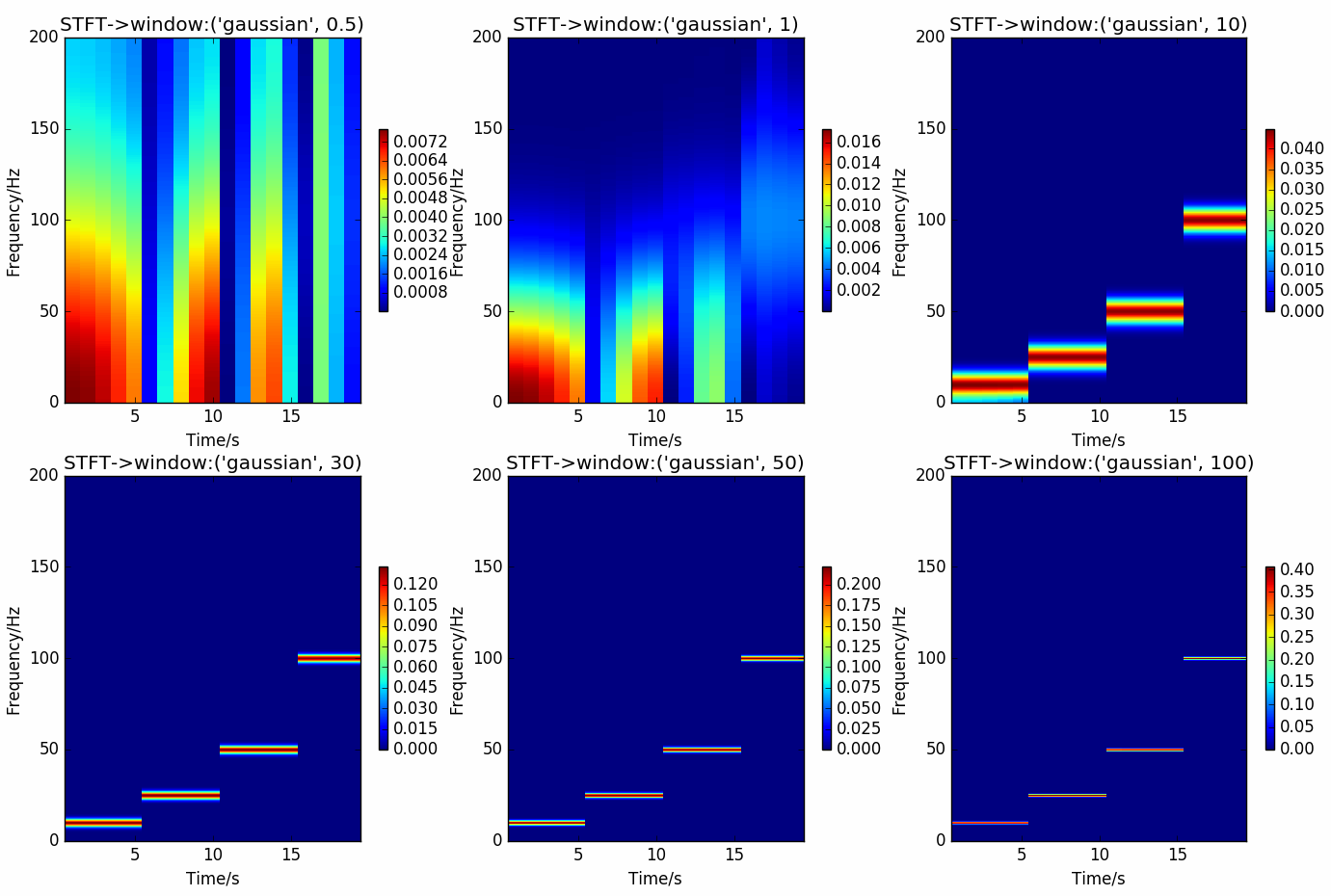
图 4.14 STFT在gauss窗, 不同std下的结果

对合成信号施加gauss窗, 窗大小取 \(1000ms\) , FFT点数取 \(2048\), 重叠点数取 \(1\) , 使用不同标准差( \(0.5, 1.0,10, 30, 50, 100\)), 然后进行STFT分析.

4. gauss窗, 不同窗大小

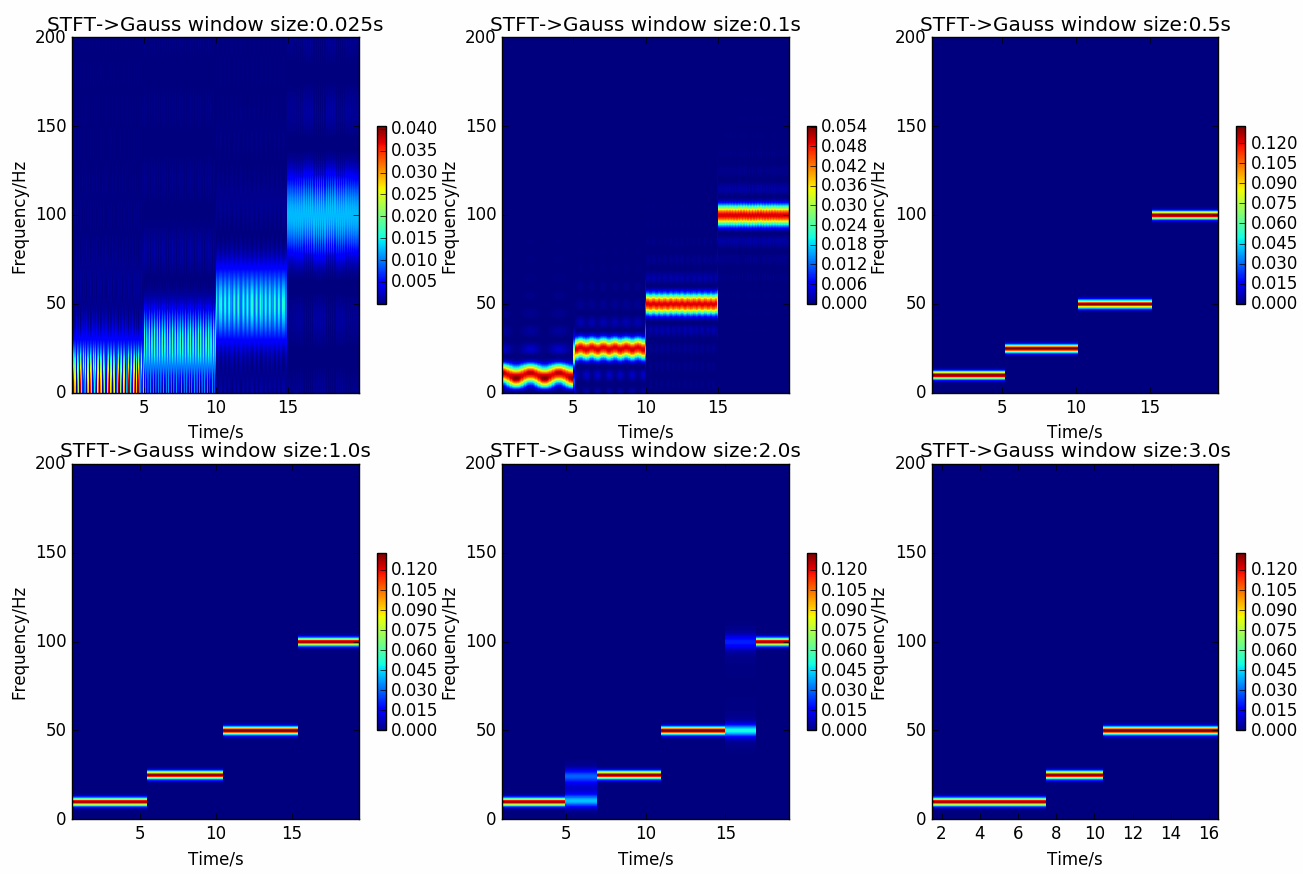
图 4.15 STFT在gauss窗, 不同窗大小下的结果

对合成信号施加gauss窗, 标准差取 \(30\) , FFT点数取 \(2048\) , 重叠点数取 \(1\) , 使用不同窗大小( \(25ms, 100ms, 500ms, 1000ms, 2000ms, 3000ms\)), 然后进行STFT分析.

对于Gauss窗, 窗过小频率难区分, 窗过大时间难区分.

5. 不同重叠点数

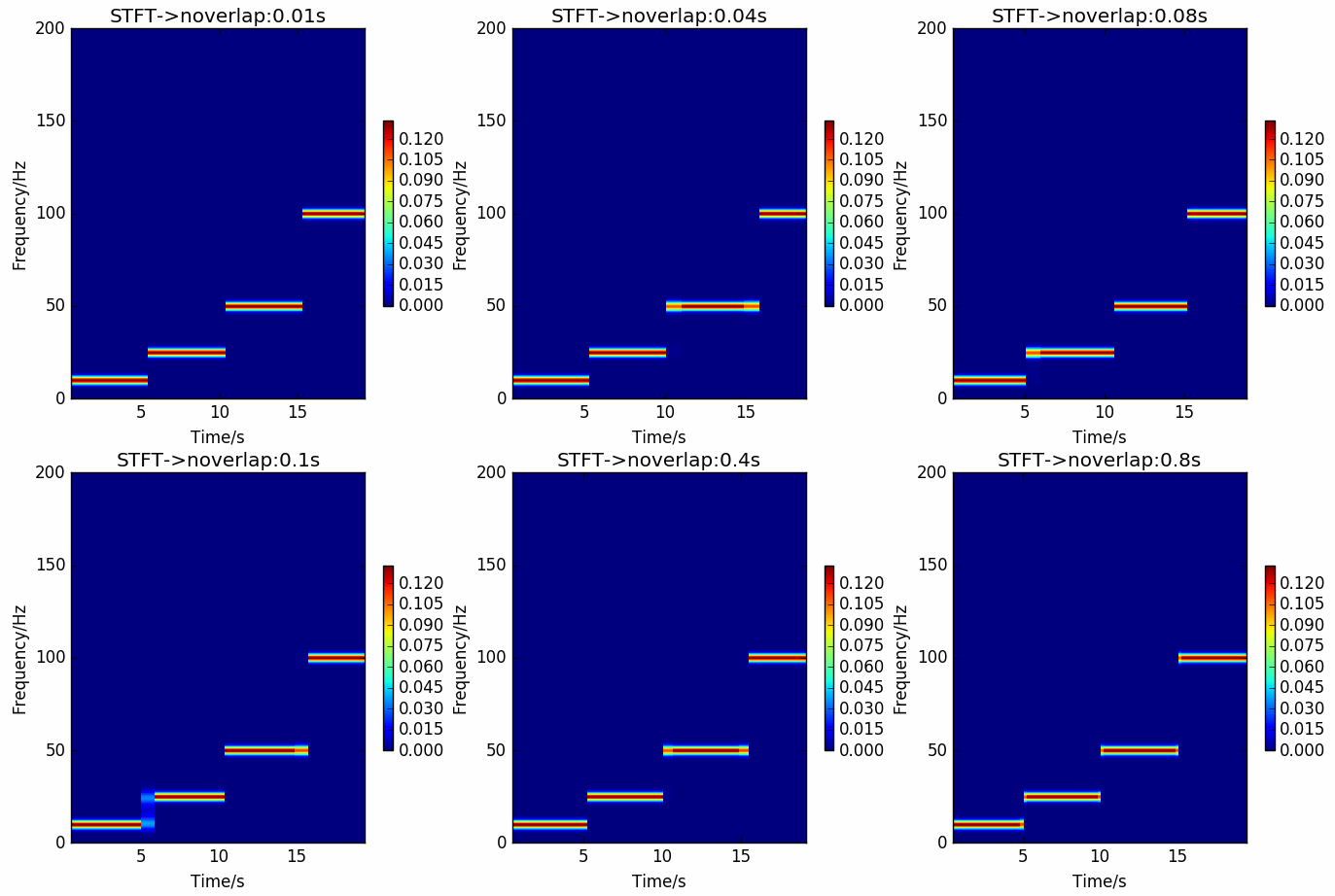
图 4.16 STFT在不同重叠点数下的结果

对合成信号施加gauss窗, 标准差取 \(30\) , 窗大小取 \(1000ms\) , FFT点数取 \(2048\) , 使用不同重叠点数, 然后进行STFT分析.

6. 不同FFT点数

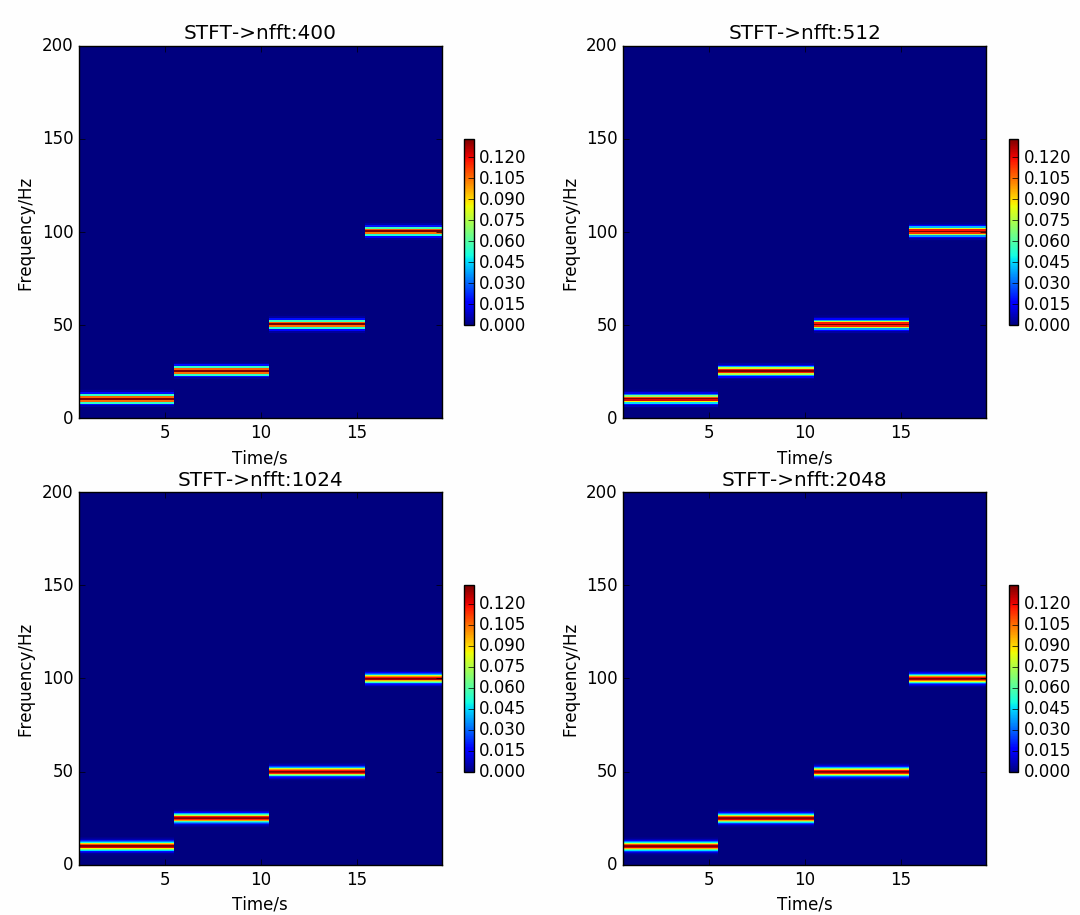
图 4.17 STFT在不同FFT点数下的结果

对合成信号施加gauss窗, 标准差取 \(30\) , 窗大小取 \(1000ms\) , 重叠点数取 \(1\) , 使用不同FFT点数, 然后进行STFT分析.

实验分析

• 对于所有窗函数, 窗大小影响较大

• 重叠点数影响较小, 但不能过大

• FFT点数影响较小, 但要大于分段长度

• 窗函数及其参数影响较大, 应仔细选取

• 对于Gauss窗, 窗过小频率难区分, 窗过大时间难区分

• 对于Gauss窗, 窗大小及标准差影响较大;

• 对于tukey, 其参数影响较小;

• 对于kaiser, 其参数影响较大.

实验2: 真实信号

语音信号