3.2.2. 窗函数及其性质

概念

类型

hamming

cosine

blackman

gaussian

tukey

kaiser

实例

窗函数比较

实验内容

产生 \(f=100Hz\) 的余弦信号 \(x(t)\) , 采样率为 \(F_s = 1000Hz\) , 采样时间 \(T_s = 0.5s\) , 对信号 \(x(t)\) 施加六种窗函数, 窗函数持续时间 \(T_w = T_s = 0.5s\) , 并对加窗前后的数据进行快速傅里叶变换.

  • hamming

  • cosine

  • blackman

  • gaussian , \({\rm{std}} = 100\)

  • tukey , \(α= 10\)

  • kaiser , \(β= 10\)

实验代码

代码文件 demo_windows_effect.py

代码 3.1 demo_windows_effect.py
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
import numpy as np
from scipy import signal
import matplotlib.pyplot as plt


f = 100
Fs = 1000
T = 0.5
Tw = 0.5

Ns = int(T * Fs)

Nw = int(Tw * Fs)

t = np.linspace(0, T, Ns)
tw = np.linspace(0, Tw, Nw)

x = np.cos(2 * np.pi * f * t)


# windn = ('tukey', 10)
# windn = ('kaiser', 10)
# windn = ('gaussian', 100)
# windn = ('hamming')
# windn = ('cosine')
windn = ('blackman')


window = signal.get_window(windn, Nw)


print(Nw, len(window))

xfft = np.fft.fft(x)
ffft = np.fft.fftfreq(x.shape[-1])

idx = 0
y = x.copy()
y[idx:idx + Nw] = x[idx:idx + Nw] * window

print(y.shape, t.shape)

plt.figure(figsize=(10, 10))
plt.subplot(221)
plt.grid()
plt.plot(t, x)
plt.title('signal')
plt.xlabel('Time/s')
plt.ylabel('Amplitude')

plt.subplot(222)
plt.grid()
plt.plot(tw, window)
plt.title('window: ' + str(windn))
plt.xlabel('Time/s')
plt.ylabel('Amplitude')

plt.subplot(223)
plt.grid()
plt.plot(t, y)
plt.title('applied window on signal')
plt.xlabel('Time/s')
plt.ylabel('Amplitude')

yfft = np.fft.fft(y)

plt.subplot(224)
plt.grid()
plt.plot(ffft * Fs, np.abs(xfft), '-b')
plt.plot(ffft * Fs, np.abs(yfft), '-r')
plt.title('FFT of signal')
plt.legend(['orignal', 'windowed'])
plt.xlabel('Frequency/Hz')
plt.ylabel('Amplitude')
plt.show()

实验结果

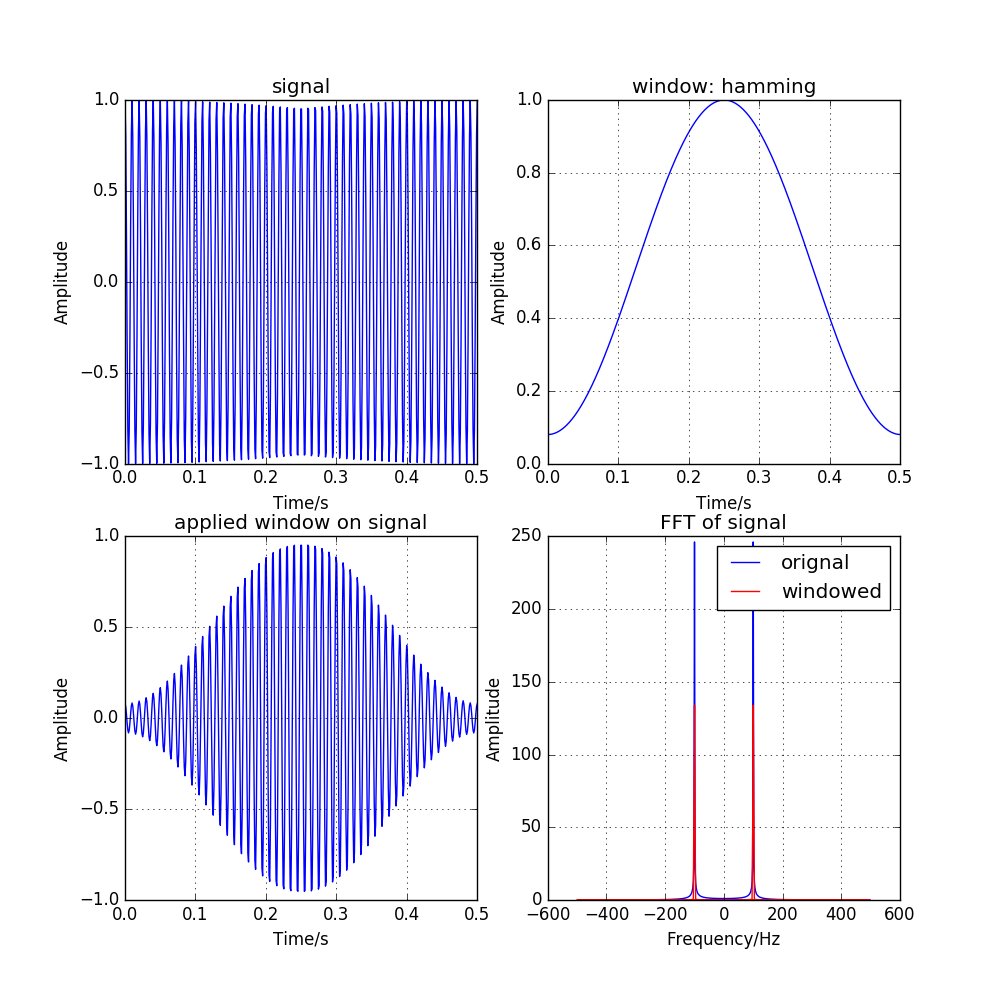
hamming function

图 3.1 effect of hamming window function

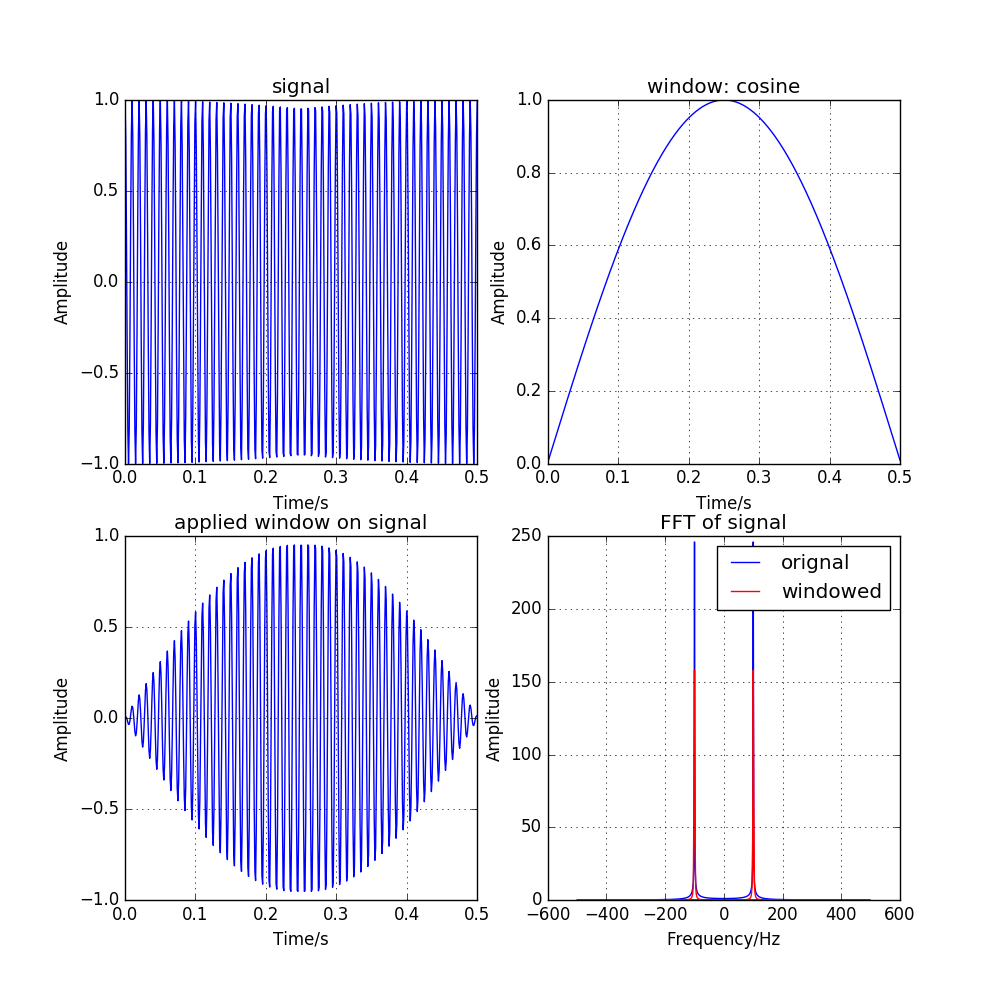
cosine function

图 3.2 effect of cosine window function

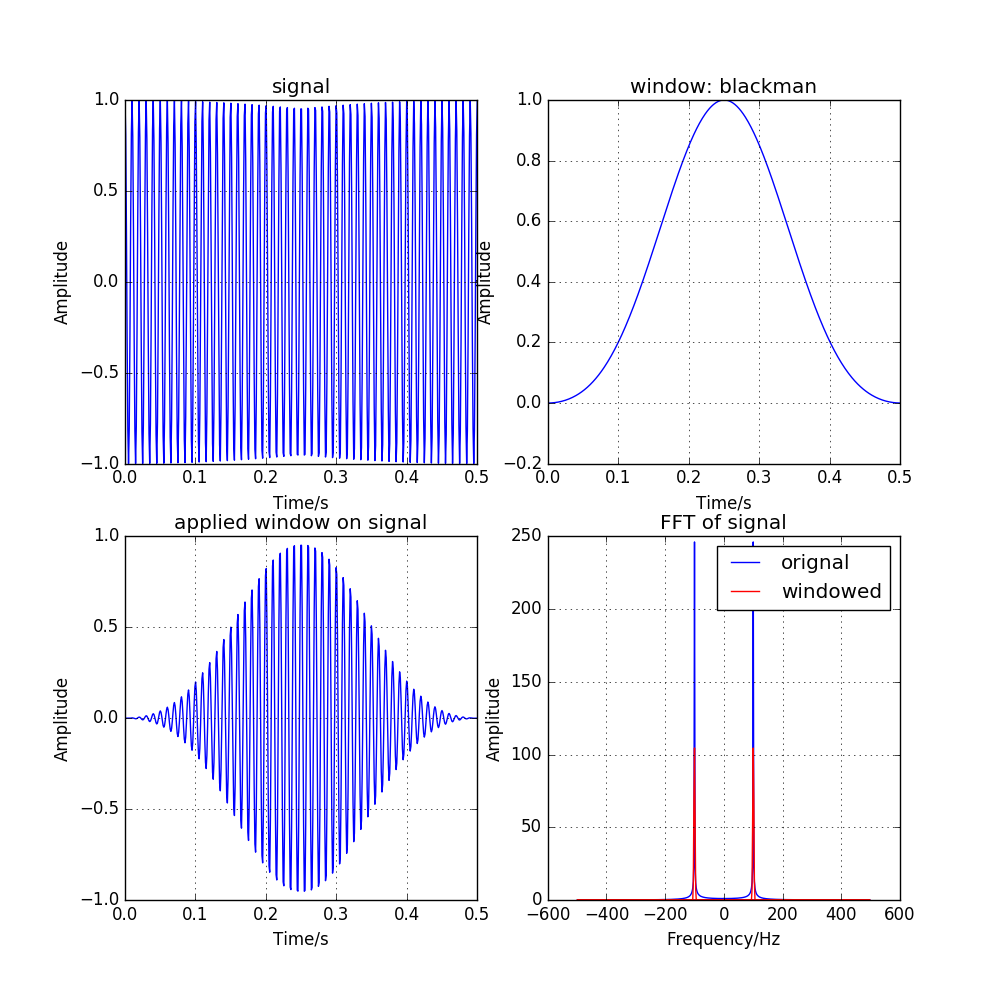
blackman function

图 3.3 effect of blackman window function

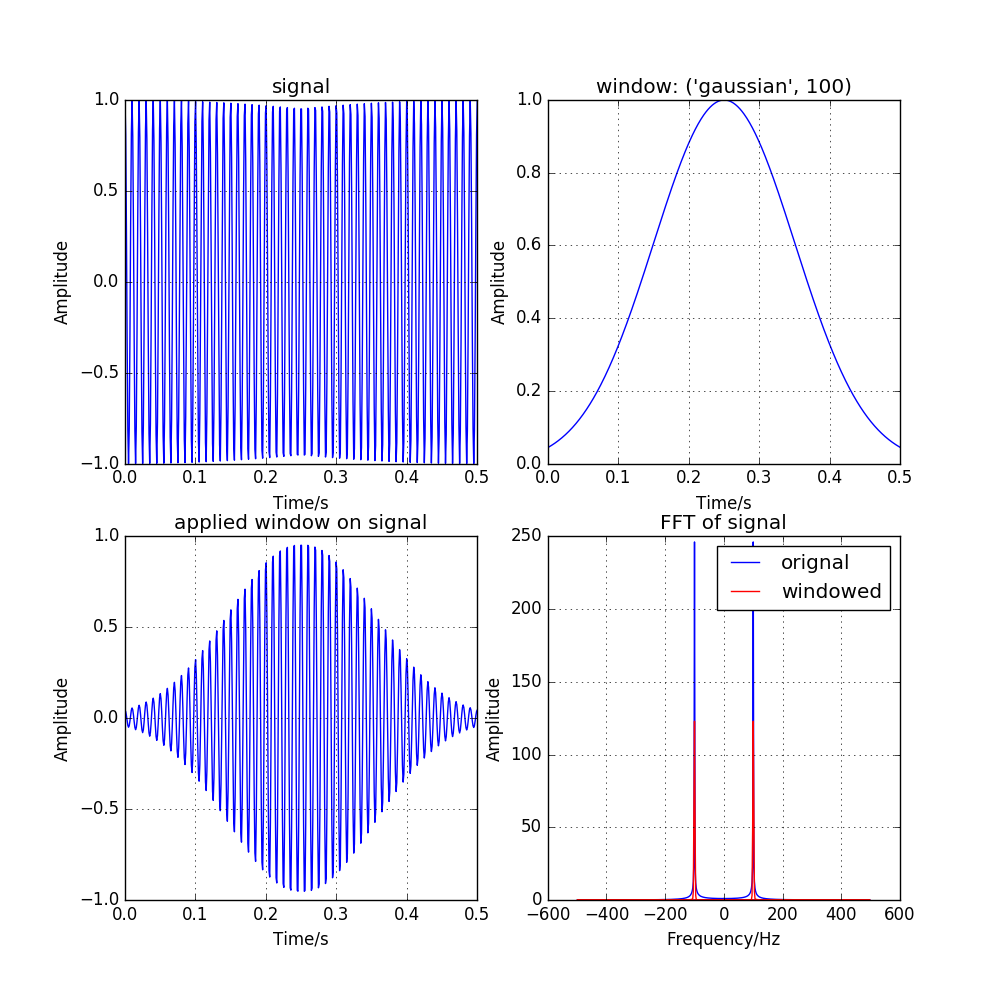
gauss100 function

图 3.4 effect of gauss window function, with \({\rm{std}} = 100\)

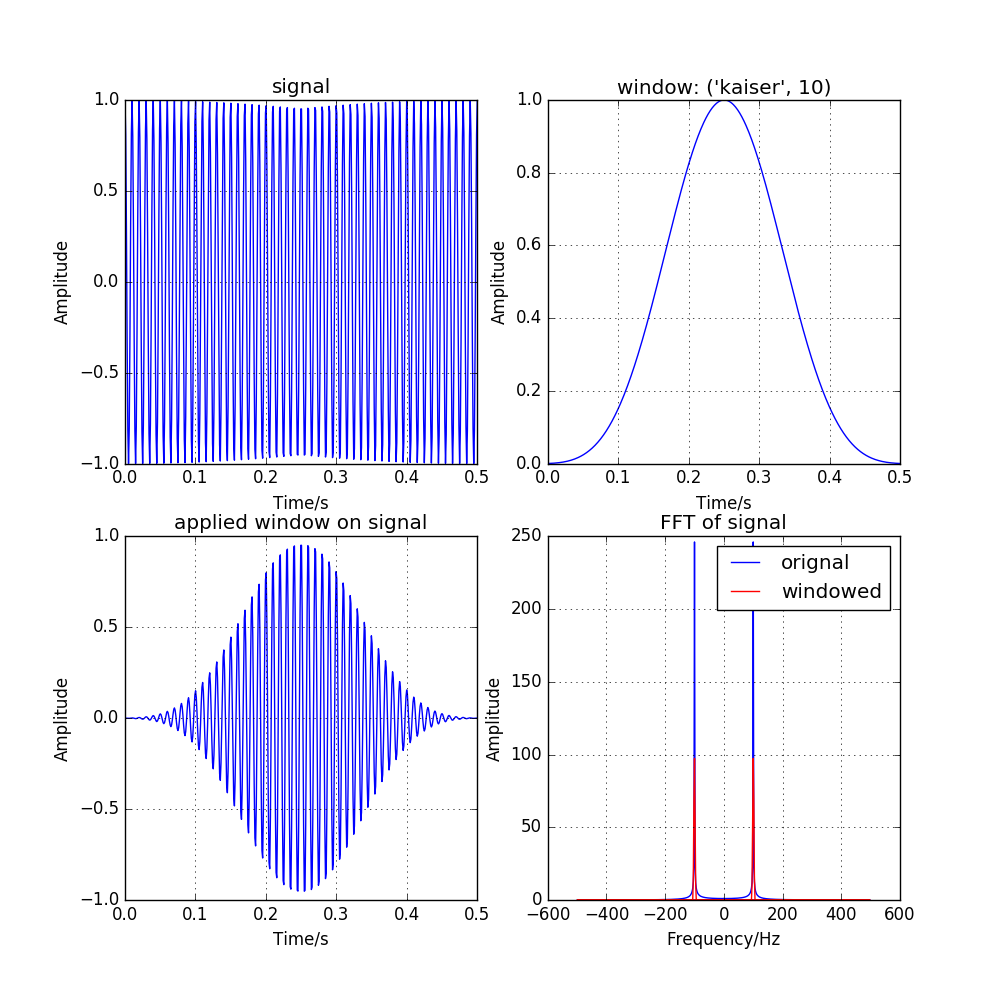
kaiser10 function

图 3.5 effect of kaiser window function, with \({\beta} = 10\)

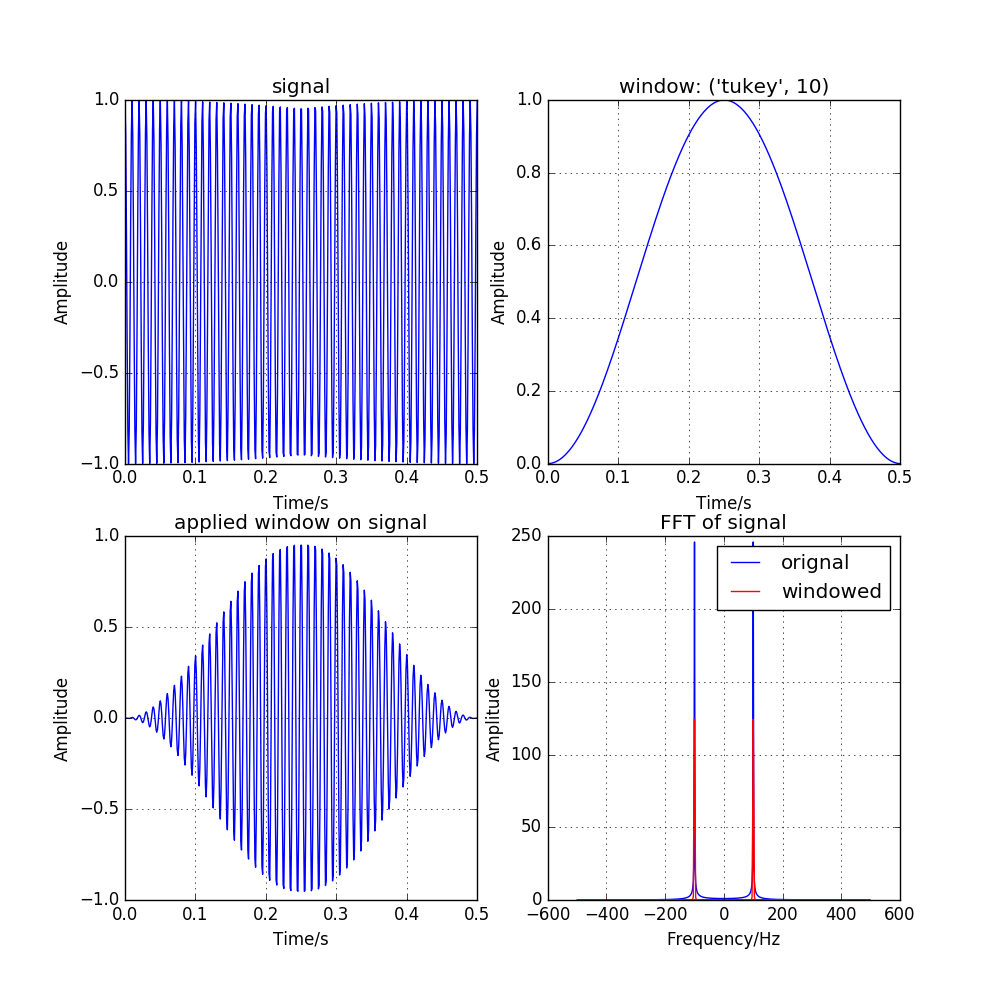
tukey10 function

图 3.6 effect of tukey window function, with \({\alpha} = 10\)