3.2.4. 傅立叶变换矩阵¶
概念与内涵¶
由上一节知, 傅里叶变换为线性变换, 傅里叶变换矩阵可以通过对单位矩阵做傅里叶变换得到.
一维傅里叶变换矩阵¶
变换矩阵推导¶
将零频率分量移到频谱中心¶
由于Matlab, Numpy等工具中的 fft() 函数未将零频率分量移到频谱中心, 这里讨论如何通过 fft() 函数得到二维傅里叶变换矩阵.
设有一维信号 \({\bm x}=[x_0, x_2, \cdots, x_{N-1}]^T\), 记一维傅里叶变换矩阵为 \({\bm F}∈{\mathbb C}^{N×N}\)
二维傅里叶变换矩阵¶
变换矩阵推导¶
二维傅里叶变换相当于对数据依次进行两个维度的傅里叶变换, 因此其变换矩阵也分为两部分.
将零频率分量移到频谱中心¶
由于Matlab, Numpy等工具中的 fft() 函数未将零频率分量移到频谱中心, 这里讨论如何通过 fft() 函数得到二维傅里叶变换矩阵.
FFT 线性变换验证实验¶
一维傅里叶变换矩阵实验¶
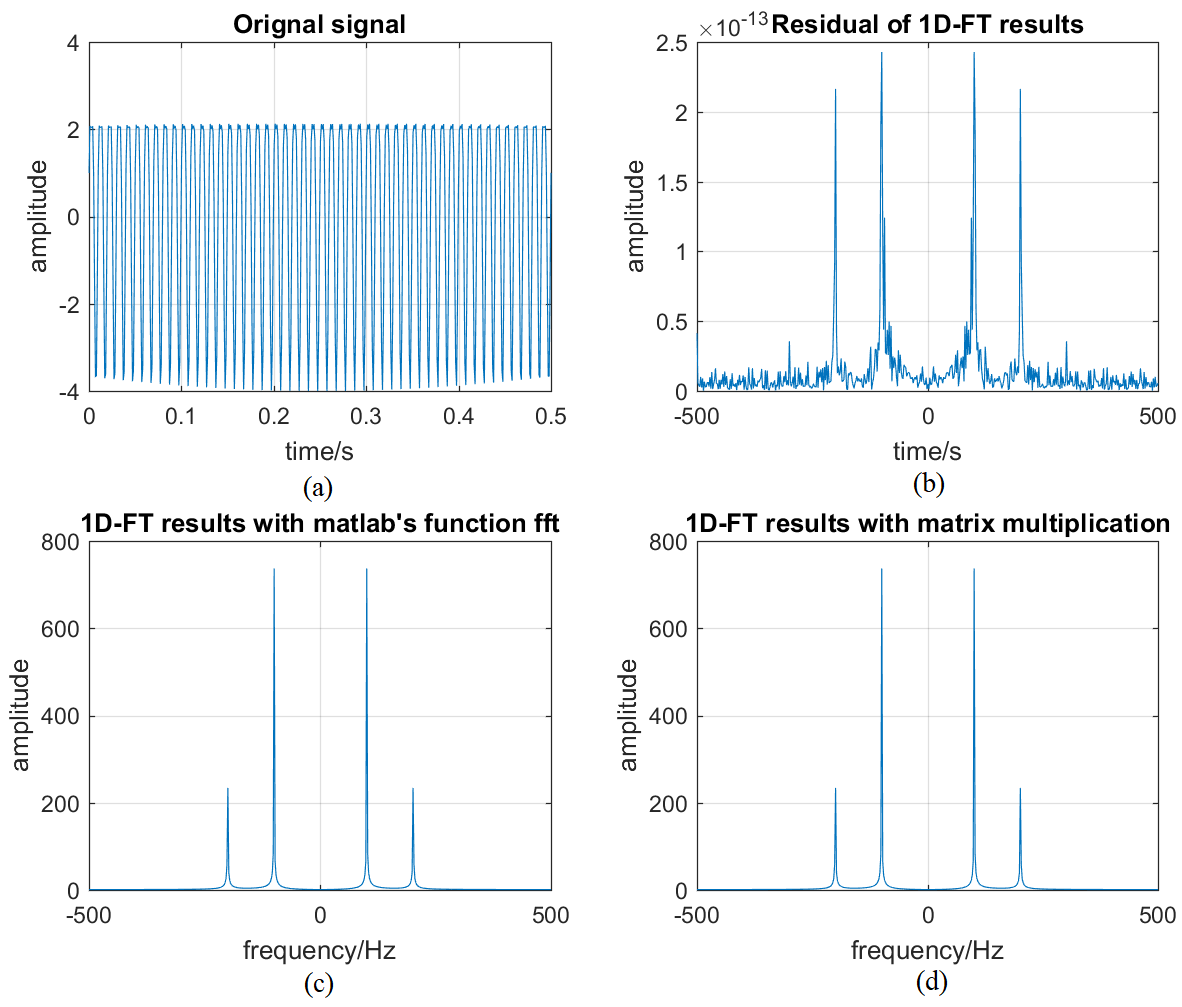
本实验验证一维 FT 变换为线性变换, 即可以通过矩阵乘法实现, 实验中仿真信号为正弦信号 \(A{\sin }(2πF_c t)\), 其中 \(F_c\) 为频率,:math:t 为时间, \(A\) 为幅度, 实验中设置 \(A=3\), \(F_c=100Hz\), 设置采样率 \(F_s= 1000Hz\), 采样时间为 \(T_s = 0.5s\). 从而采样点数为 \(N_s=500\), 对单位矩阵 \({\bm I}∈ {\mathbb R}^{N_s×N_s}\) 做傅里叶变换得到傅里叶变换矩阵, 与信号相乘即将信号变换到频域.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 | Ts = 0.5;
Fs = 1000;
Fc = 100;
A = 3;
Ns = uint32(Fs * Ts);
t = linspace(0, Ts, Ns)';
x = A * sin(2*pi*Fc*t);
f = linspace(-Fs/2.0, Fs/2.0, Ns);
y1 = fft(fftshift(x));
y1 = fftshift(fft(x));
I = eye(Ns);
M = fftshift(fft(I));
y2 = M * x;
residual = abs(y1- y2);
figure(1)
subplot(221)
plot(t, x)
xlabel('time/s')
ylabel('amplitude')
title('Orignal signal')
grid on
subplot(222)
plot(f, residual)
xlabel('time/s')
ylabel('amplitude')
title('Residual of 1D-FT results')
grid on
subplot(223)
plot(f, abs(y1))
xlabel('frequency/Hz')
ylabel('amplitude')
title('1D-FT results with matlab''s function fft')
grid on
subplot(224)
plot(f, abs(y2))
xlabel('frequency/Hz')
ylabel('amplitude')
title('1D-FT results with matrix multiplication')
grid on
|
二维傅里叶变换矩阵实验¶
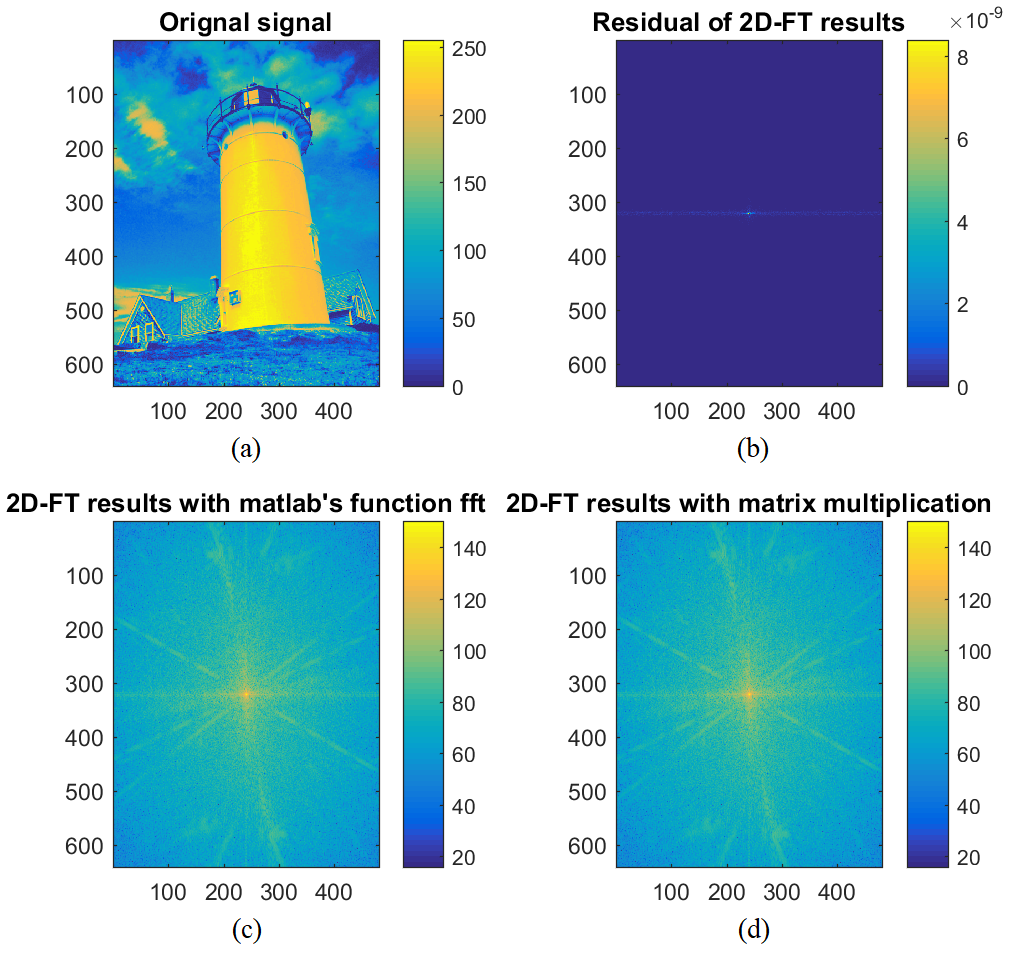
本实验验证二维 FT 变换为线性变换, 即可以通过矩阵乘法实现, 实验中信号为图像, 对单位矩阵 \({\bm I}∈ {\mathbb R}^{N_s×N_s}\) 的行和列分别做傅里叶变换得到行和列上的傅里叶变换矩阵, 与信号相乘即将信号变换到频域.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 | clear all
close all
X = imread('lighthouse.png');
% X = imread('cameraman.tif');
X = double(X(:, :, 1));
[H, W] = size(X);
Y1 = fftshift(fft(fftshift(X, 1), [], 1), 1);
Y1 = fftshift(fft(fftshift(Y1, 2), [], 2), 2);
MH = fftshift(fft(fftshift(eye(H), 2), [], 1), 1);
MW = fftshift(fft(fftshift(eye(W), 1), [], 2), 2);
Y2 = MH * X;
Y2 = Y2 * MW;
residual = abs(Y1- Y2);
figure(1)
subplot(221)
imagesc(X)
title('Orignal signal')
colorbar();
subplot(222)
imagesc(residual)
title('Residual of 2D-FT results')
colorbar();
subplot(223)
imagesc(20*log10(abs(Y1)))
title('2D-FT results with matlab''s function fft')
colorbar();
subplot(224)
imagesc(20*log10(abs(Y2)))
title('2D-FT results with matrix multiplication')
colorbar();
|