3.2. 距离与速度测量

3.2.1. 三角波测距与测速

频率调制连续波 (Frequency Modulated Continuous Wave, FMCW) 测距与测速, 发射一信号频率呈现三角波变化的调频连续波, 利用时延及多普勒效应实现测距与测速。其原理可由下图给出:

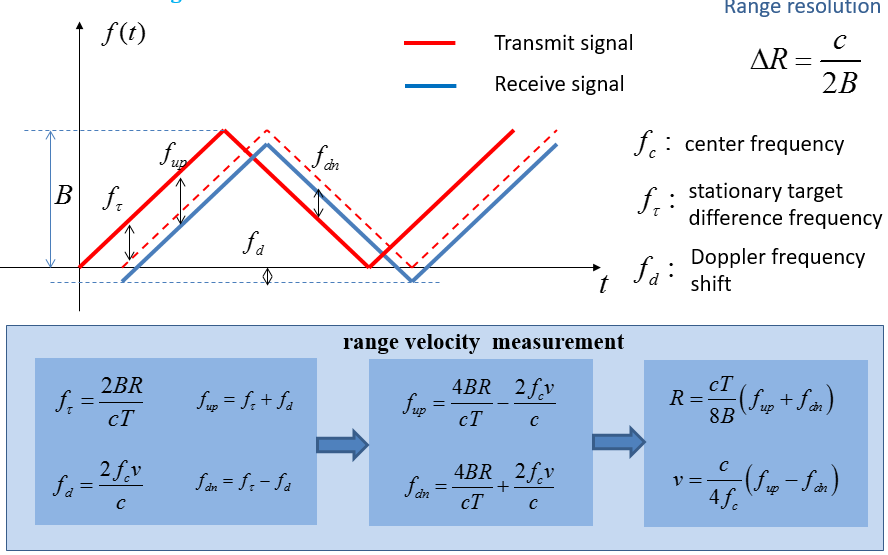
图 3.30 三角波测距与测速

其中:

• \(c\) 为光速;

• \(B\) 为调制带宽;

• \(T_m\) 为调制周期;

• \(R\) 为目标与雷达间的距离;

• \(f_c\) 为载频;

• \(f_{\tau}\) 为静止目标差频;

• \(f_d\) 为运动目标产生的多普勒频移;

3.2.2. 锯齿波测距

锯齿波测距原理示意图如下:

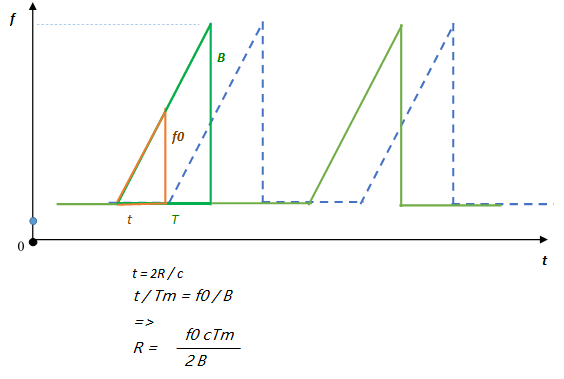
图 3.31 锯齿波测距

其中:

• \(f_0\) 为目标静止时的差频;

• \(f_d\) 为多普勒差频, 可通过FFT获得;

• \(B\) 为调制带宽;

• \(T_m\) 为调制周期;

• \(c\) 为光速;

• \(R\) 为距离;

• \(v\) 为速度;

3.2.3. 距离速度模糊

高脉冲重复频率信号

距离模糊: 目标回波延迟时间大于脉冲重复周期, 同一距离

• 倍乘法解模糊

• DFS解模糊

• 三角波变频法

在多普勒速度不模糊时, MTD求得的结果准确

• 复合体制测速;

测速模糊

由香浓定理, 要满足测速不模糊, 需要采样频率 \(f_r\) 不小于两倍的由速度产生的多普勒频率, 即满足 \({f_r} < 2f_{d_{max}}\) , 由此可以推导出采样周期 (即脉冲重复周期), 具体计算过程如下:

图 3.32 MTD多普勒测速模糊分析

解决方案

距离速度解耦

采用复合体制, 即 FMCW + CW, 如调制波采用梯形波;

多目标配对

• MTD可以实现多目标中, 同一目标的距离与速度的配对 (计算量、存储量较大)

• 典型梯形波配对法 (存在虚假目标情况)

• 变周期梯形波配对法 (计算量稍大)