6.4. 基于局部感受野的模糊极速学习机¶
6.4.1. 简介¶
现实世界中, 每个训练样本的重要性不一, 通常一些训练样本比另外一些更重要, 我们希望有意义的样本被正确分类, 而不关心噪声样本是否被错分 [1] . 在基于局部感受野的极速学习机 (Local Receptive Fields based Extreme Learning Machine, ELM-LRF) 上引入模糊性, 使得模型对噪声更加鲁邦, 得到基于局部感受野的模糊极速学习机 (Local Receptive Fields based Fuzzy Extreme Learning Machine, FELM-LRF).
提示
模糊集合的概念参见章节 模糊集合
有关基于局部感受野的极速学习机参见章节 基于局部感受野的极速学习机.
6.4.2. FELM-LRF原理¶
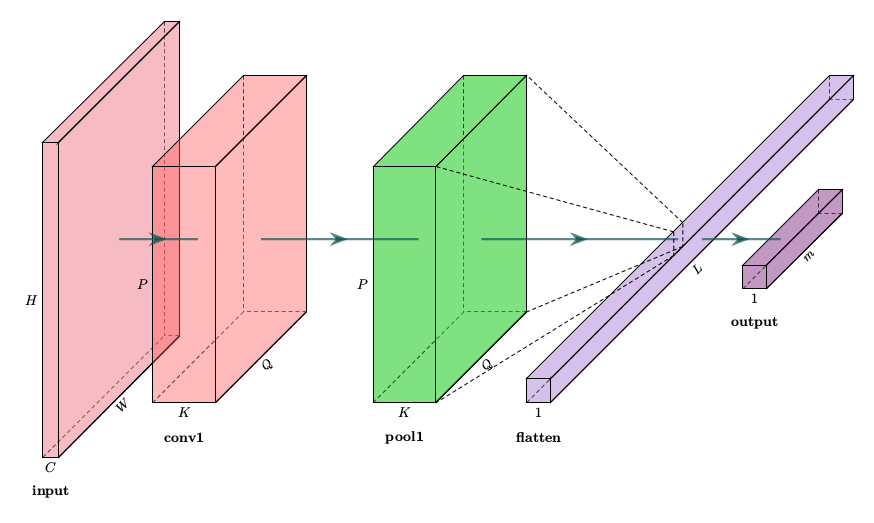
图 6.10 Framework of FELM-LRF.¶
对于分类问题, 假设有训练样本集 \(\tilde{\mathbb S} = \{({\bm x}_i, {\bm y}_i, u_i)\}_{i=1}^N\), 其中, \(N\) 为样本数目, \(u_i \in {\mathbb R}\) 为样本 \({\bm x}_i\in{\mathbb R}^n\) 对应的隶属度, \({\bm y}_i\) 为 \({\bm x}_i\) 对应的标签, 在损失函数中引入隶属度, 从而有 FELM-LRF 的优化问题
其中, \(\sigma_{1}>0, \sigma_{2}>0, \quad p, q>0\) , \({\bm U} = {\rm diag}(u_1, u_2, \cdots, u_N) \in {\mathbb R}^{N \times N}\) 为由所有训练样本的隶属度组成的对角矩阵, \(\bm{\beta}\in{\mathbb R}^{L \times m}\) 输出层权重矩阵, \({\bm T}\in {\mathbb R}^{N\times m}\) 为由样本标签组成的 one-hot 矩阵, 满足
记 \({\bm H}_F = {\bm U}{\bm H}\), \({\bm T}_F = {\bm U}{\bm T}\) , 则 FELM-LRF 的优化问题 式.6.3 变为
当 \(\sigma_{1}=\sigma_{2}=p=q=2\) 时, 容易求得 式.6.4 的解为
其中, \({\bm H}_F = {\bm U}{\bm H}\), \({\bm T}_F = {\bm U}{\bm T}\).