2.2.1. Sinc插值¶
Sinc插值原理¶
Sinc插值 ( Sinc Interpolation ) 也叫 Whittaker–Shannon interpolation 是一种从真实离散序列构造一个连续时间带限函数的方法, 即根据实际离散采样点逼近连续函数.
\[x(t) = \sum_{n=-\infty}^{+\infty}{x[n]{\rm sinc}\left(\frac{t-nT}{T}\right)}\\
~~~~ = \sum_{n=-\infty}^{+\infty}{x[n]{\rm sinc}\left(\frac{t}{T}-n\right)}
\]
其中, \(T\) 为采样间隔, \({\rm sinc}(t) = \frac{{\rm sin}(\pi t)}{\pi t}\) 称为归一化的 \({\rm sinc}\) , 与数学中定义的 \({\rm sinc}(x) = \frac{{\rm sin}(x)}{x}\) 不同.
上式可以表示为卷积形式:
\[x(t) = \left(\sum_{n=-\infty}^{+\infty}x[n]\cdot \delta(t-nT)\right)*{\rm sinc}\left(\frac{t}{T}\right),
\]
相当于采用一个低通滤波器滤波.
实验与分析¶
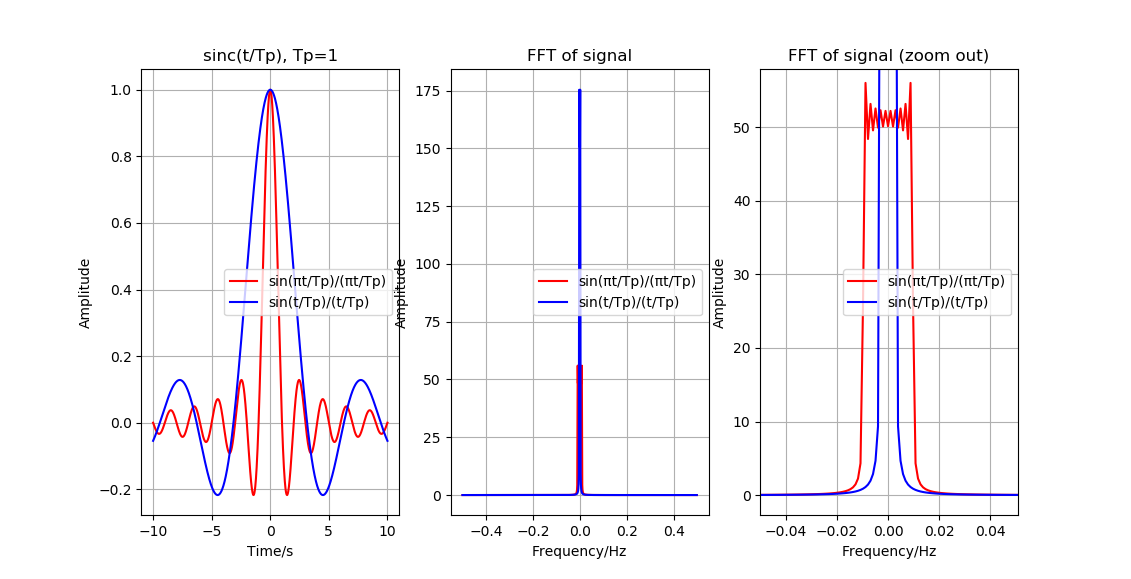
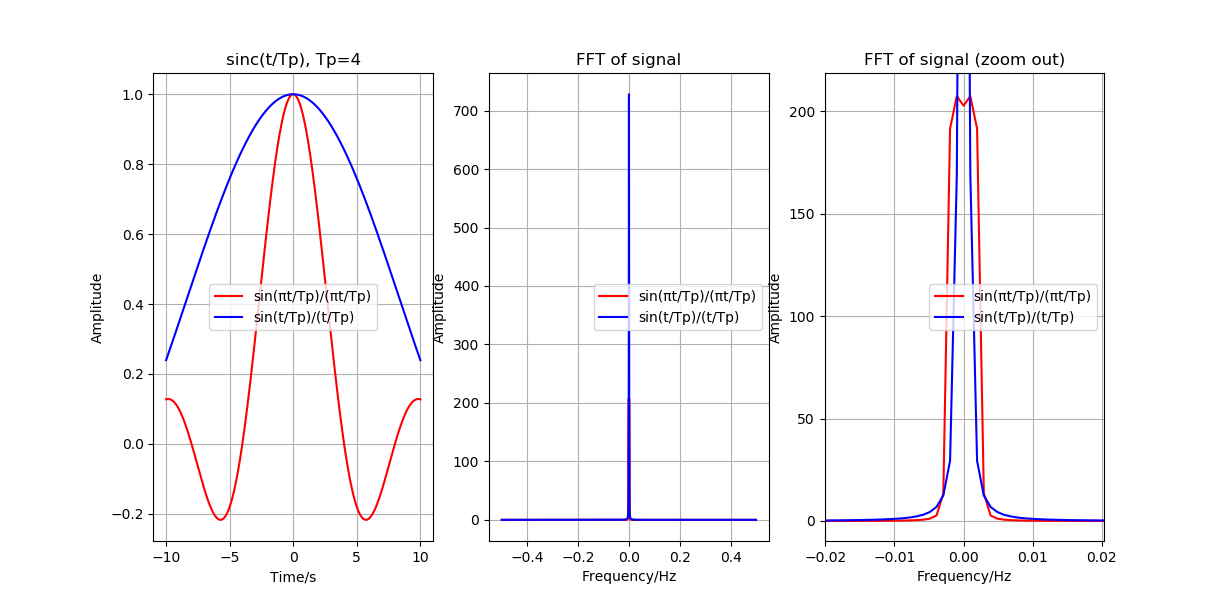
sinc 函数特性¶
实验代码¶
本书Python实现代码, 参见文件 demo_SincProperties.py .
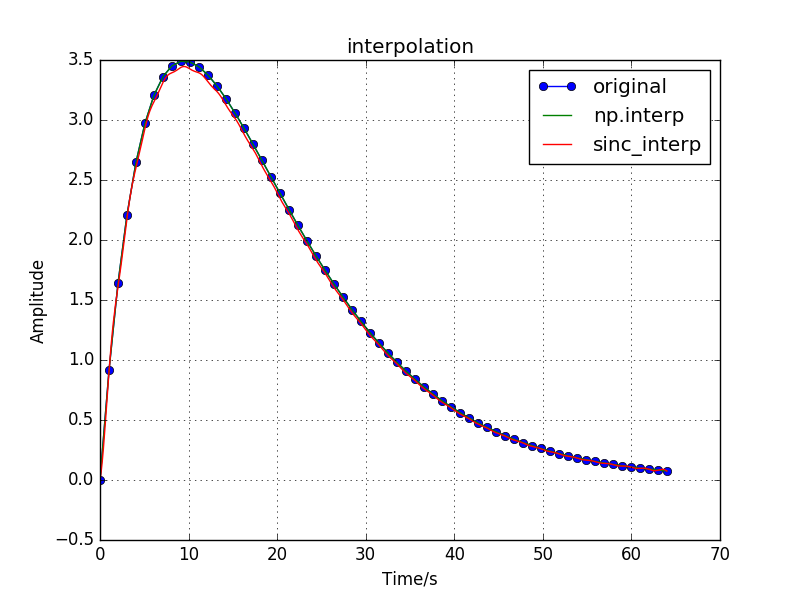
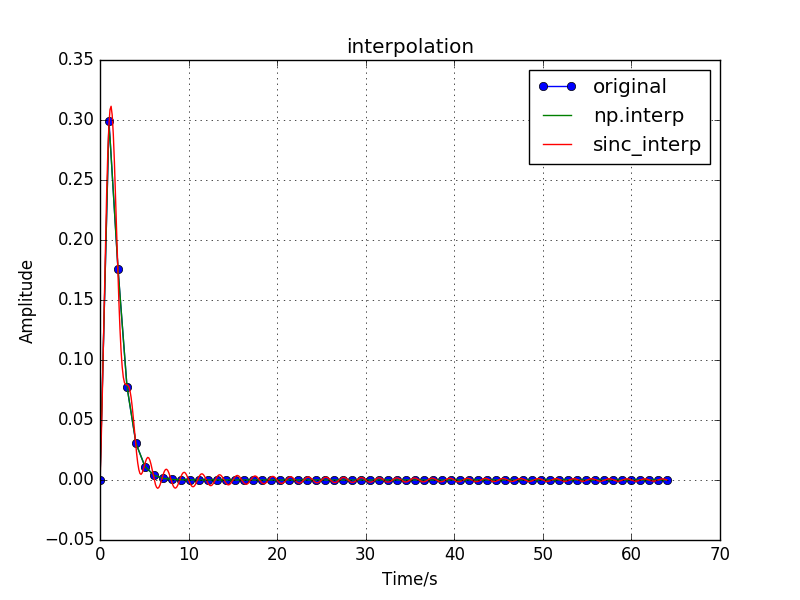
sinc 插值¶
实验代码¶
可参考代码:
“MATLAB code by Dr. John S. Loomis” –> sinc_interp.m
function y = sinc_interp(x,u)
m = 0:length(x)-1;
for i=1:length(u)
y(i) = sum(x.*sinc(m- u(i)));
end
demo_sinc_interp.m
a = 0.9;
N = 64;
n = 0:N-1;
x = n.*a.^n;
plot(n,x);
y = fft(x);
k= 0:N/2;
plot(k/N,abs(y(1:N/2+1)));
s = linspace(0,63,512);
x2 = sinc_interp(x,s);
plot(s(1:256), x2(1:256), '-r');
title('sinc interpolated')
hold
xi = interp1(n, x, s);
plot(s(1:256),xi(1:256),'k');
title('interp1 interpolated')
plot(n(1:N/2),x(1:N/2),'o');
legend({'sinc interpolated', 'interp1 interpolated', 'orignal'})
hold off
本书Python实现代码, 参见文件 demo_SincInterpolation.py .