2.1. 三角波泄漏

2.1.1. 三角波泄漏分析

发射机信号泄漏是FMCW毫米波雷达比较严重的问题.

泄漏原因

三角波泄漏的根本原因是由于 VCO调频的非线性 , 调频的同时存在着调幅. 这时的发射信号不再是一纯粹的调频波, 而是调幅调频波, 该调幅调频波被单端混频器的GaAS肖特基势垒二极管和后面的低通滤波器构成的包络检波电路所检波, 其调幅信号被检波出来, 叠加在有用信号上, 形成泄漏三角波.

解决方法

  • 要从根本上抑制三角波泄漏, 应该尽量提高VCO的性能, 改进 RF 中 VCO 的线性度和减小扫描功率非线性, 尽量减小调频时存在的寄生调幅.

  • 在中频电路中, 可采用固定的高通或带通滤波器来抑制三角波的泄漏. 但因三角波频率和有用中频信号很接近, 高通或带通的实现比较困难. 也可以采用 频域动态压缩方法, 它不仅有效抑制三角波泄漏, 而且在一定程度上可以替代AGC, 简化电路设计, 提高系统灵敏度, 适用于近距离探测. 用由电容和电感组成的近线性巴特沃斯高通滤波器可以实现.

  • 数字处理部分, 可采用信号时频分析、短时FFT分析和 多种自适应处理方法 等来有效抑制三角波泄漏, 提高系统性能.

频域动态压缩方法

源于频域对消思想,它利用泄漏三角波和有用中频信号在频域中的不同, 抑制三角波信号, 增强有用信号: 同时利用FMWC毫米波雷达中频频率(幅度)与距离的关系, 对不同频率的有用信号进行不同的压缩处理, 使得其最终各个频率对应的输出信号幅度相同, 一定程度上达到替代AGC的目的. 下图为一种压缩网络与其对应的幅频特性

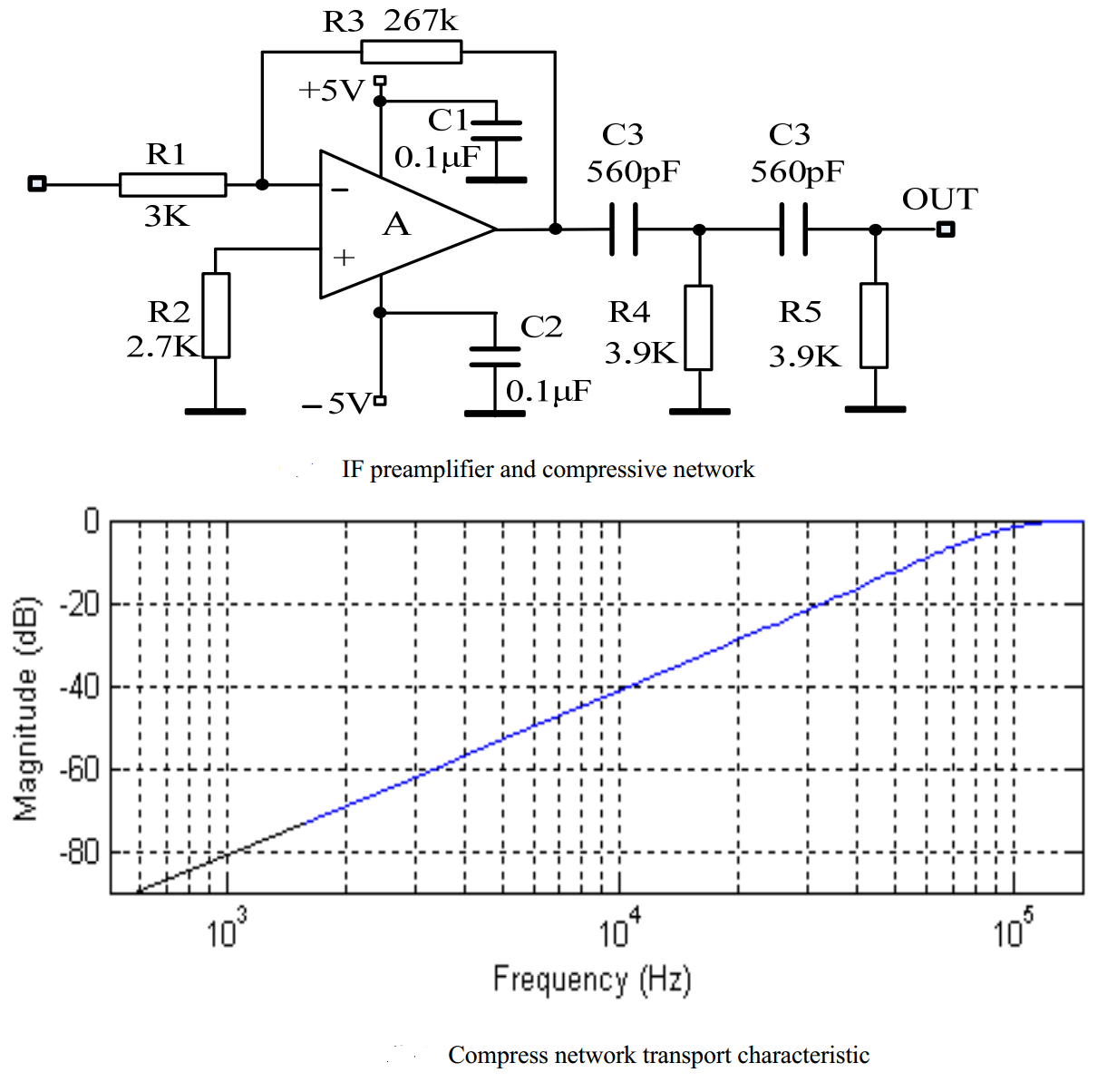
../../../_images/compressnet.png

图 2.37 频域压缩网络及其幅频特性

自适应处理方法

注解

关于自适应滤波器中的参考信号: 自适应滤波器中的参考信号(期望信号)是如何获取的

在许多情况下, 一个宽带信号既受到周期性干扰的污染, 又没有外部参考输入可以利用. 此时, 可以直接从原始输入引出, 接入一具有固定延迟的延迟线, 则可得到类似得参考输入支路. 延迟 △必须选得足够长, 以使参考输入中的宽带信号分量和原始输入中的宽带信号分量去相关. 而干扰分量因其周期性, 将仍然是彼此相关的. 经过对消器后, 在系统输出中去掉了原始输入中的可预测部分而留下了其中的不可预测分量.

../../../_images/adapterfilter_noref.png

图 2.38 没有参考输入的周期干扰自适应对消

2.1.2. 三角波泄漏自适应对消验证

实现方式及结果对比

自己实现

采用最小均方（Least Mean Square, LMS）误差准则实现参数调优, 核心代码如下:

function [ output, err, w ] = adaptfilterlms( input, desired, param )

LEN = length(input);

% 设计自适应滤波器
M = param.M;                       % 滤波器阶数
u = param.mu;                      % step

w = ones(M,1);                     % weight

output = zeros(LEN,1);
err = output;

for k = M:LEN
    wn(:, k-M+1) = w;
    output(k) = input(k-M+1:k)'*w;
    err(k) = desired(k) - output(k);
    w = w + 2*u*err(k).*input(k-M+1:k);          % update

end

end
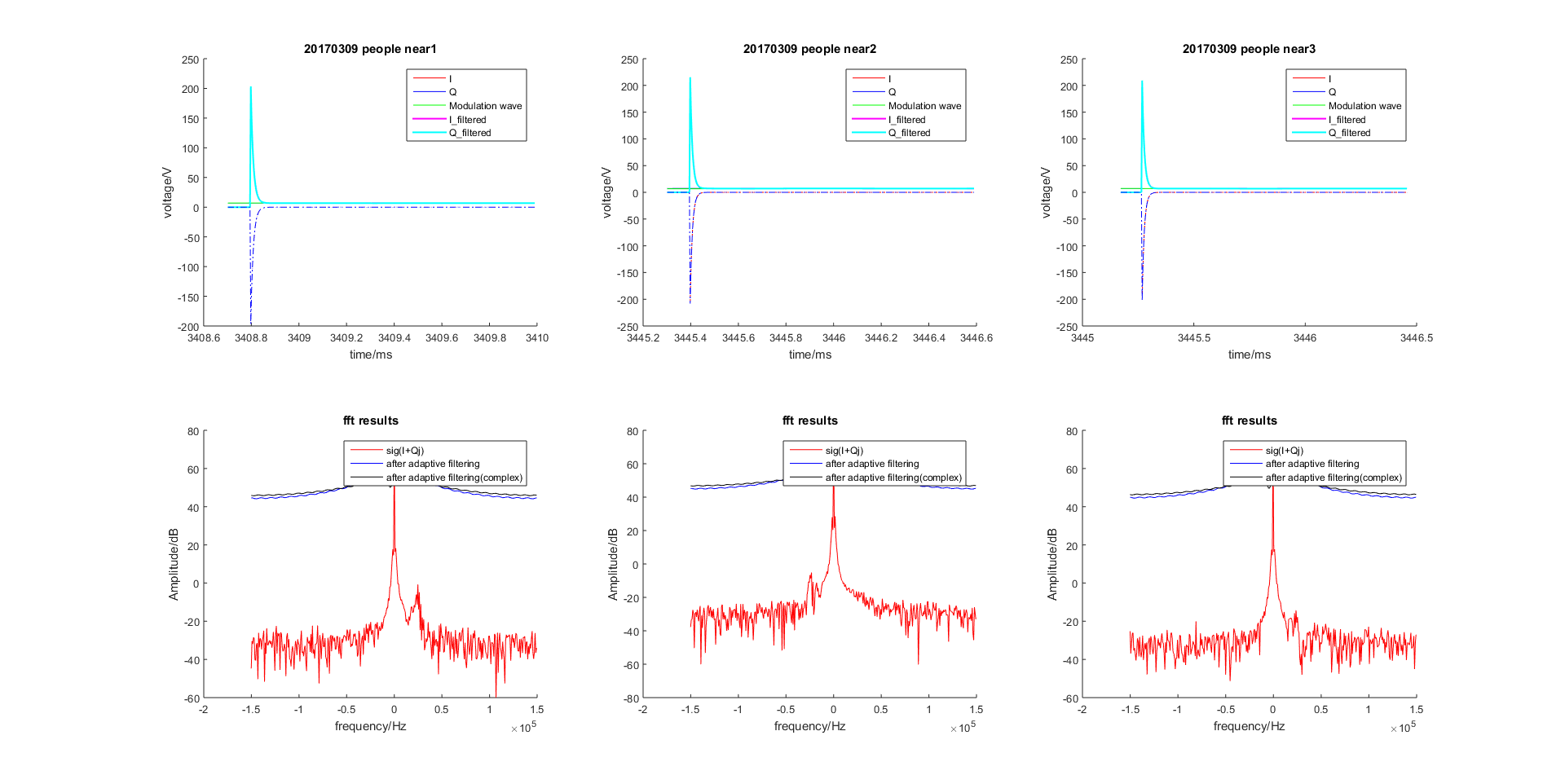
../../../_images/byme_itprocess.png

图 2.39 自适应滤波迭代过程（虚线为误差）

../../../_images/byme_stationary.png

图 2.40 自适应滤波稳态过程（虚线为误差）

matlab实现

这里借用 MATLAB DSP 库中提供的 dsp.LMSFilter 函数实现. 核心代码如下:

function [ output, err, w ] = adaptivefilter( noised, ref, param, method )

if nargin < 4
    h = adaptfilt.lms(param.M, param.mu);
    [output, err] = filter(h, ref, noised);
else
    hlms = dsp.LMSFilter('Length',param.M, ...
   'Method', method,...
   'AdaptInputPort',true, ...
   'StepSizeSource','Input port', ...
   'WeightsOutputPort',true);

    [output, err, w] = step(hlms, ref, noised, param.mu, 1);
end

end
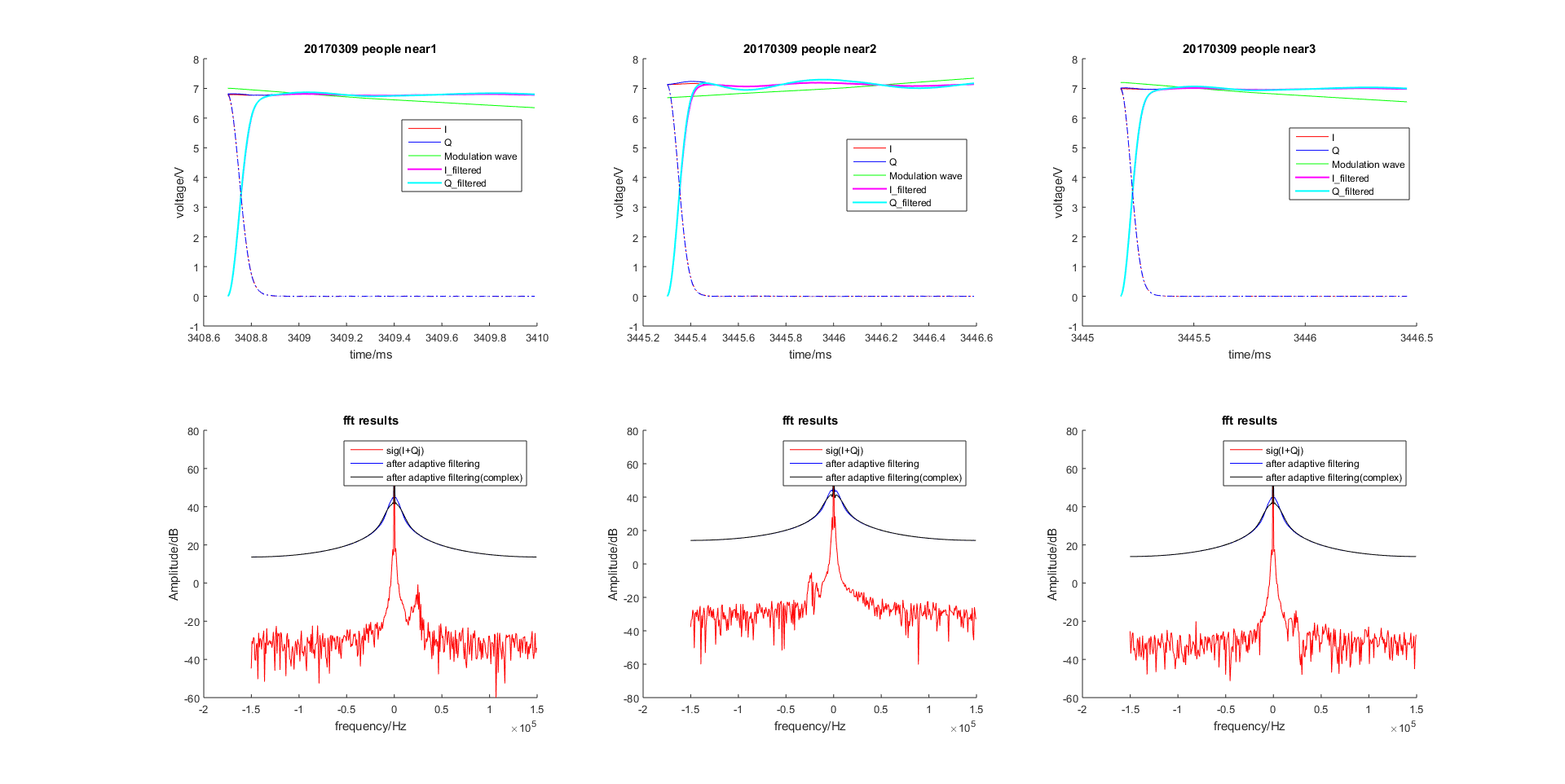
../../../_images/matlabDSP_itprocess.png

图 2.41 自适应滤波迭代过程（虚线为误差）

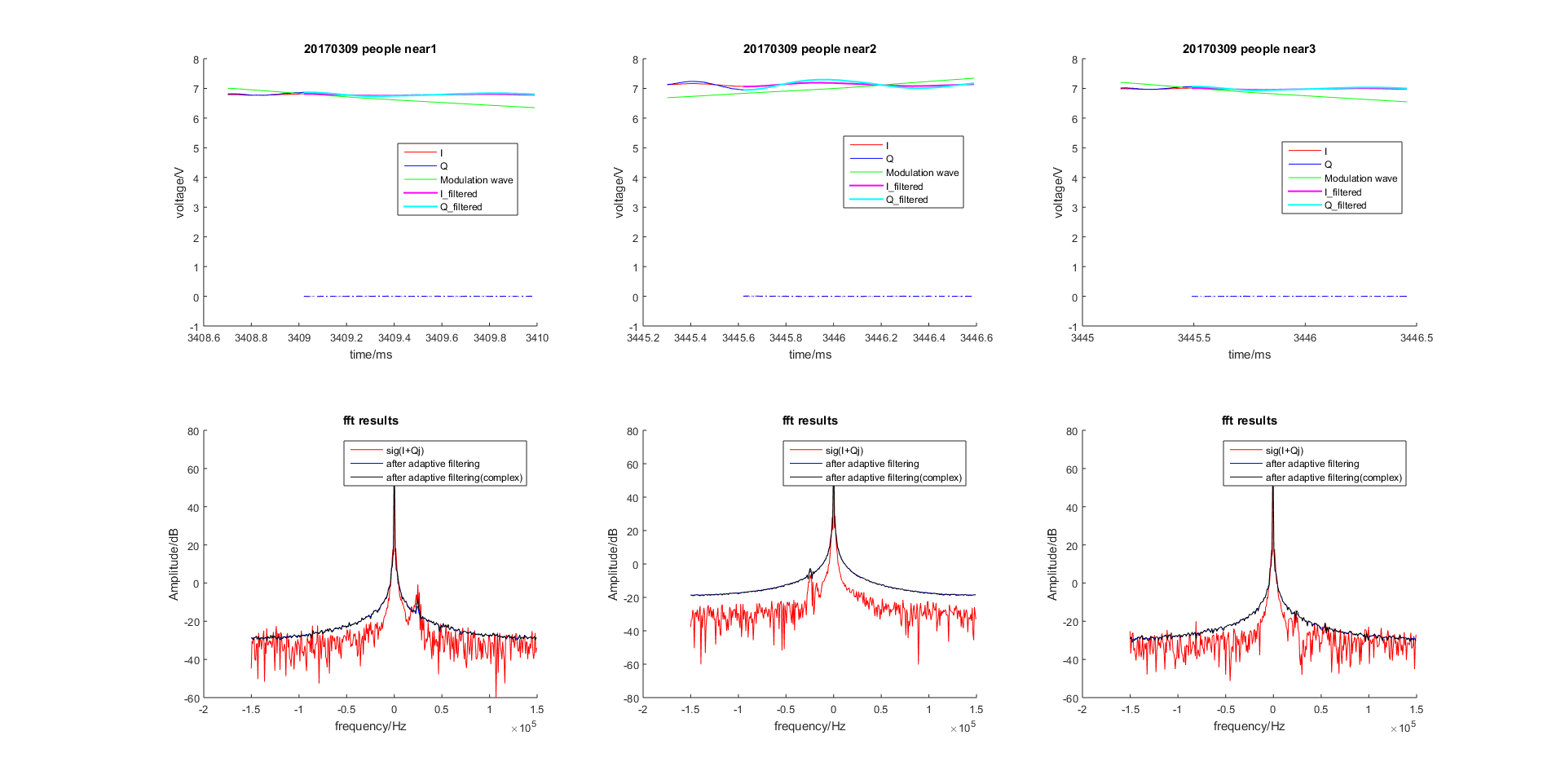
../../../_images/matlabDSP_stationary.png

图 2.42 自适应滤波稳态过程（虚线为误差）

以下仅示意稳态后的结果.

结果对比

../../../_images/byme.png

图 2.43 自己编程实现验证结果图示

../../../_images/matlabDSP.png

图 2.44 采用 MATLAB 自带函数库验证结果图示

滤波效果分析

参考信号

  • 三角波调制信号重复频率为 1/4e-3 = 250Hz;

  • 滤波器阶数: param.M = 30 ;

  • 步长: param.mu = 0.0001 .

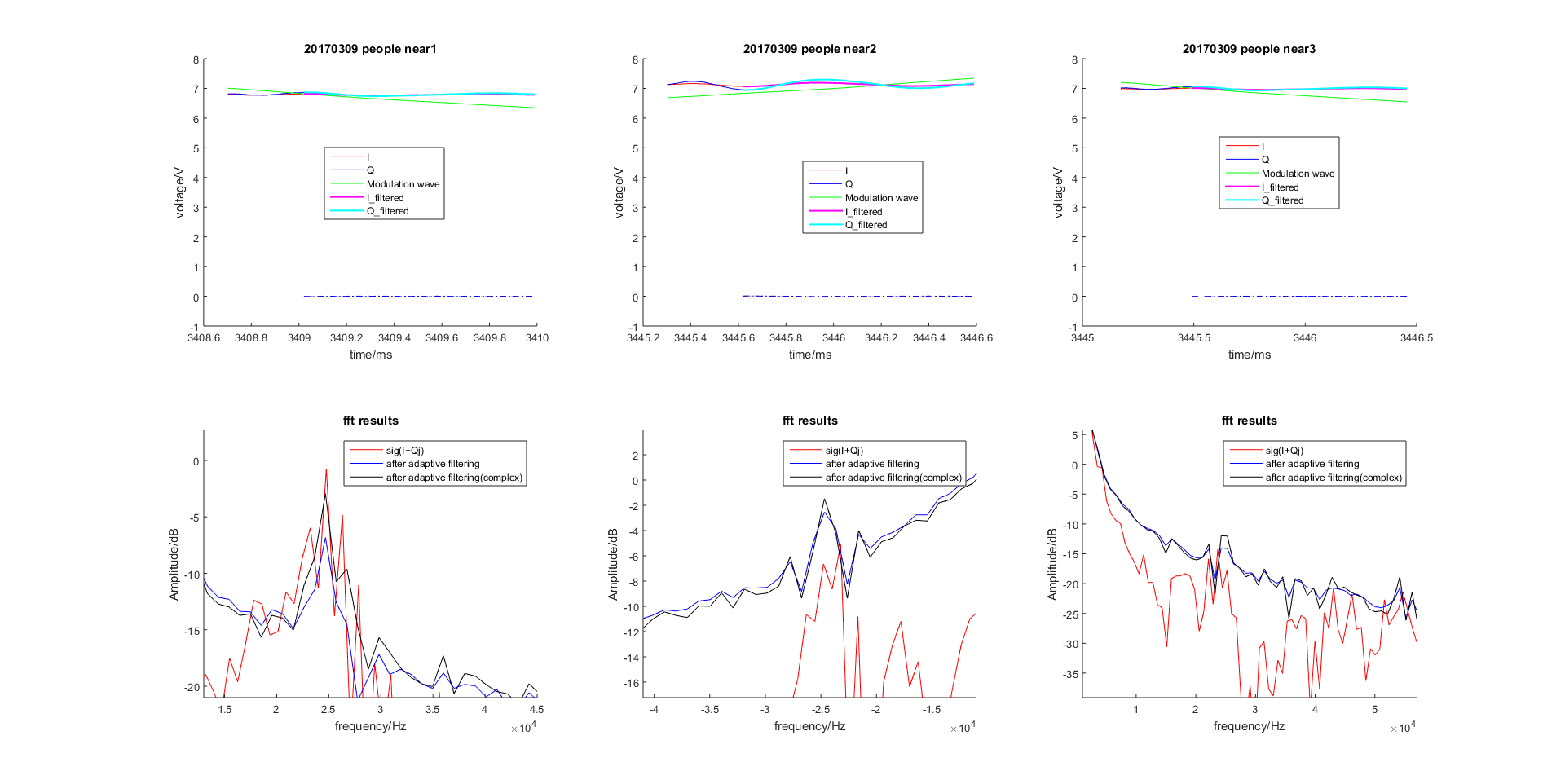
  1. 带噪雷达回波时延信号

../../../_images/matlabDSP_LMS_radarecho_m30_mu1e-4_refDelayRadarEcho_stationary.png

图 2.45 基于LMS的自适应滤波器滤波效果（参考信号为带噪雷达回波时延信号）

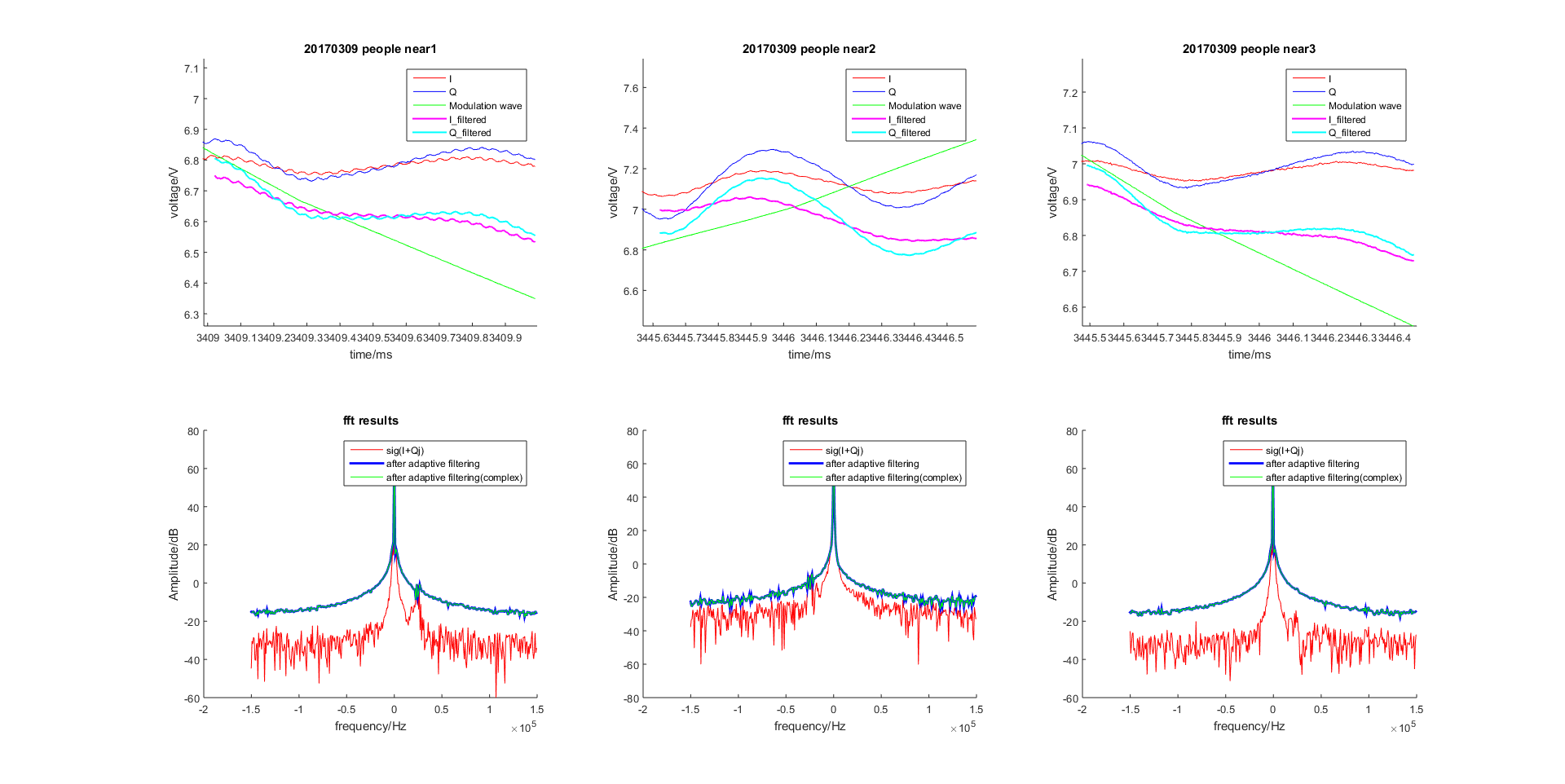
../../../_images/matlabDSP_NormLMS_radarecho_m30_mu1e-4_refDelayRadarEcho_stationary.png

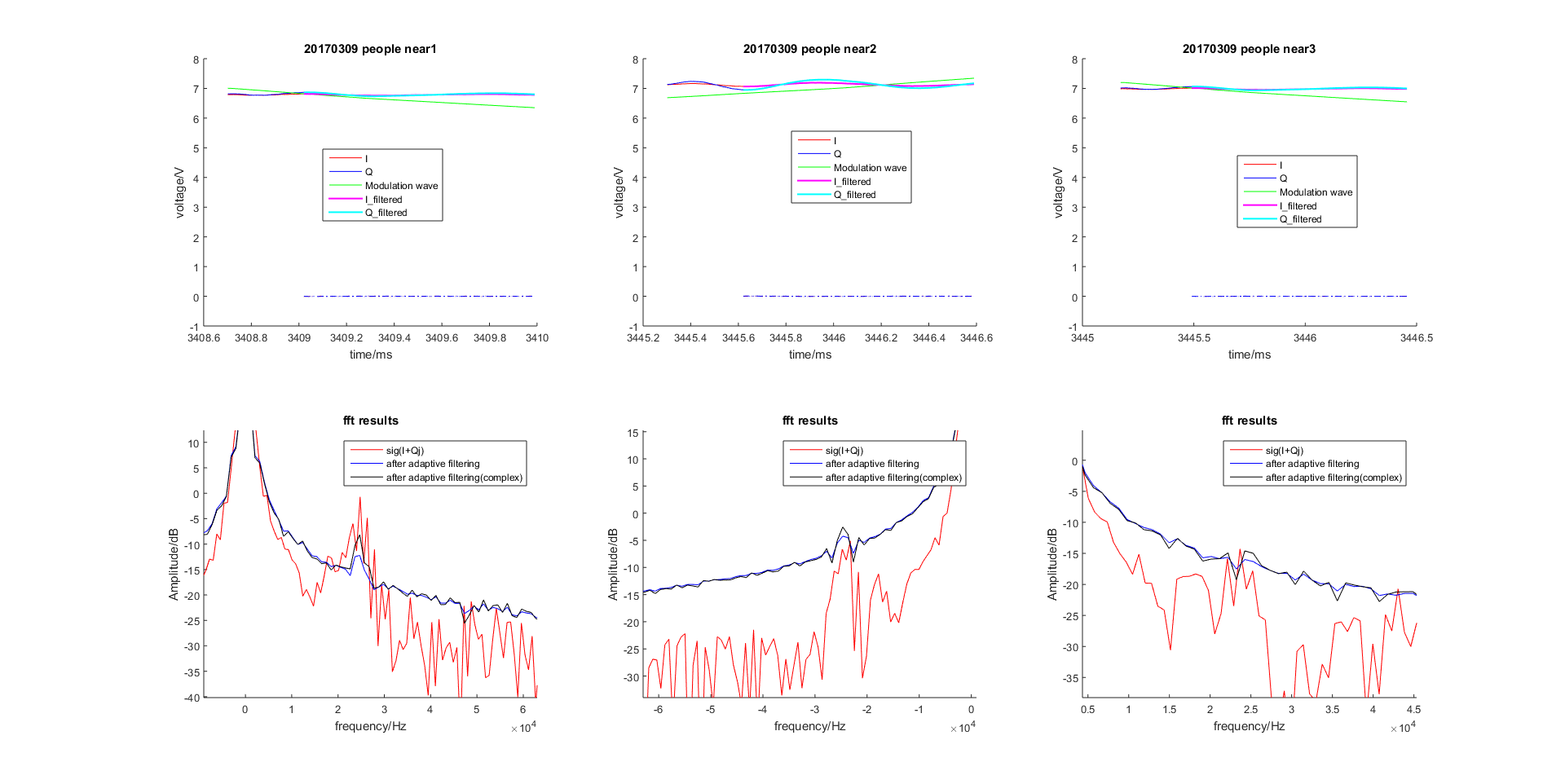
图 2.46 基于Normalized LMS的自适应滤波器滤波效果（参考信号为带噪雷达回波时延信号）

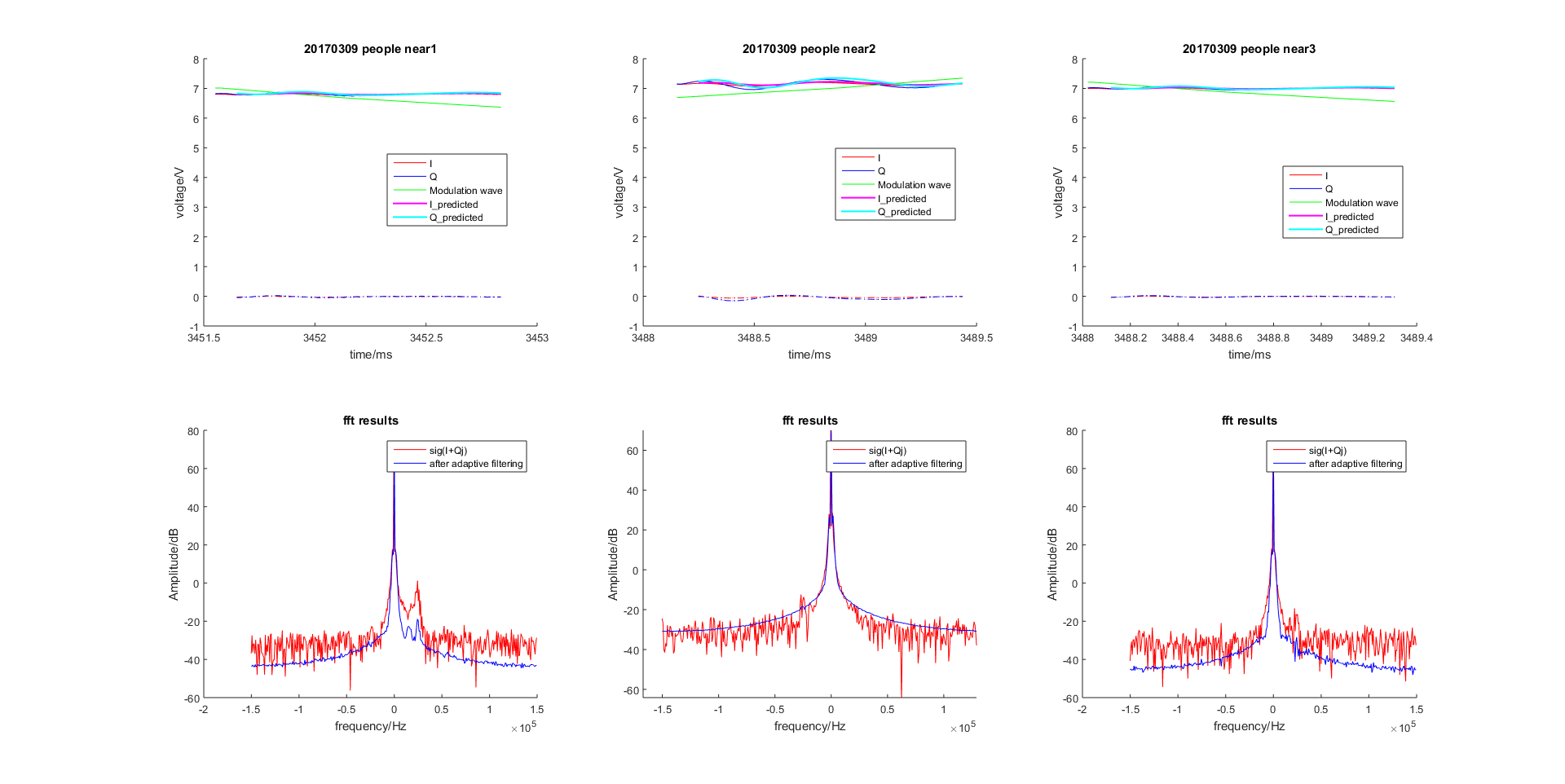
  1. 调制信号

../../../_images/matlabDSP_LMS_radarecho_m30_mu1e-4_refModuWave_stationary.png

图 2.47 基于LMS的自适应滤波器滤波效果（参考信号为调制信号）

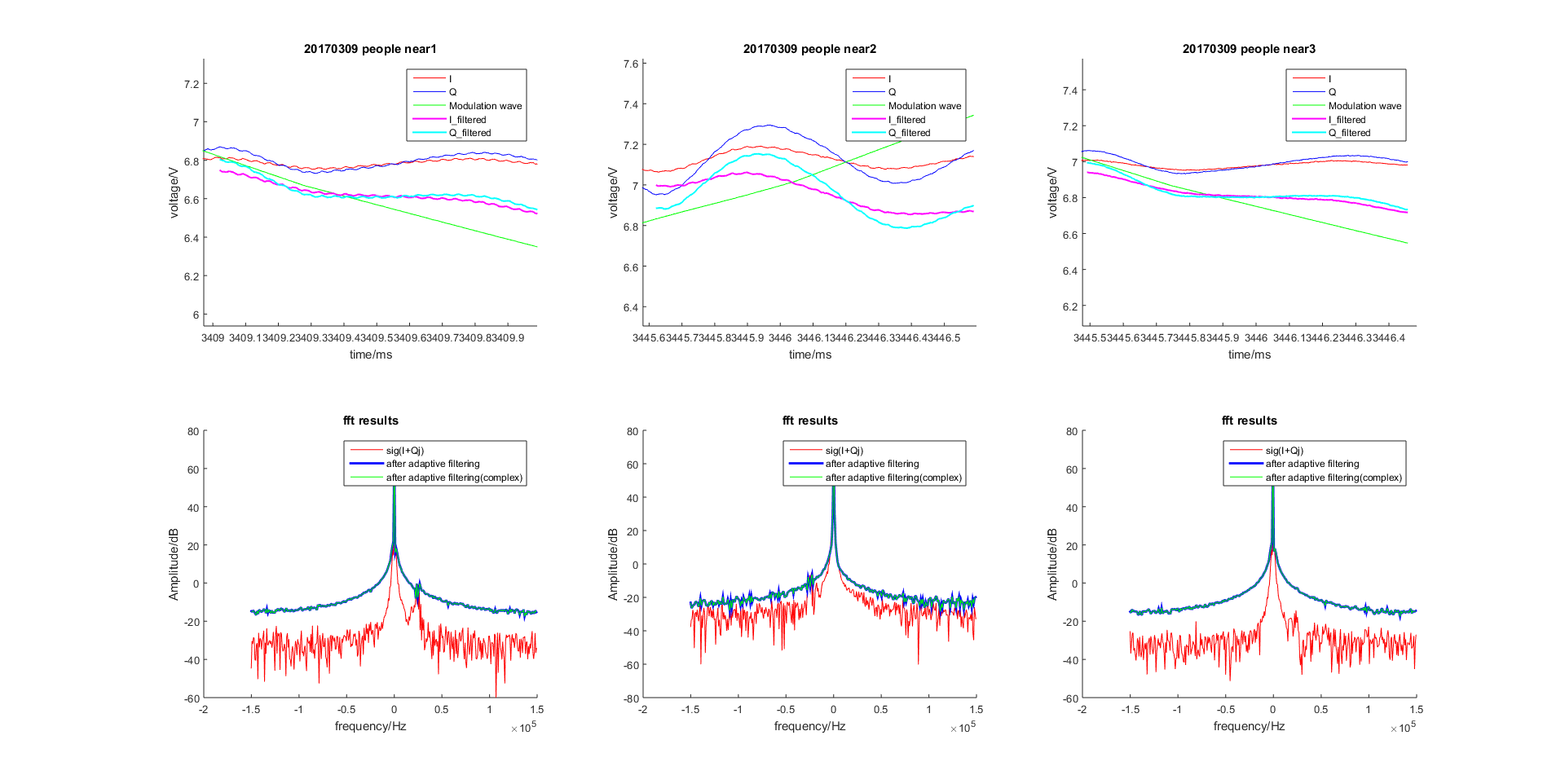
../../../_images/matlabDSP_NormLMS_radarecho_m30_mu1e-4_refModuWave_stationary.png

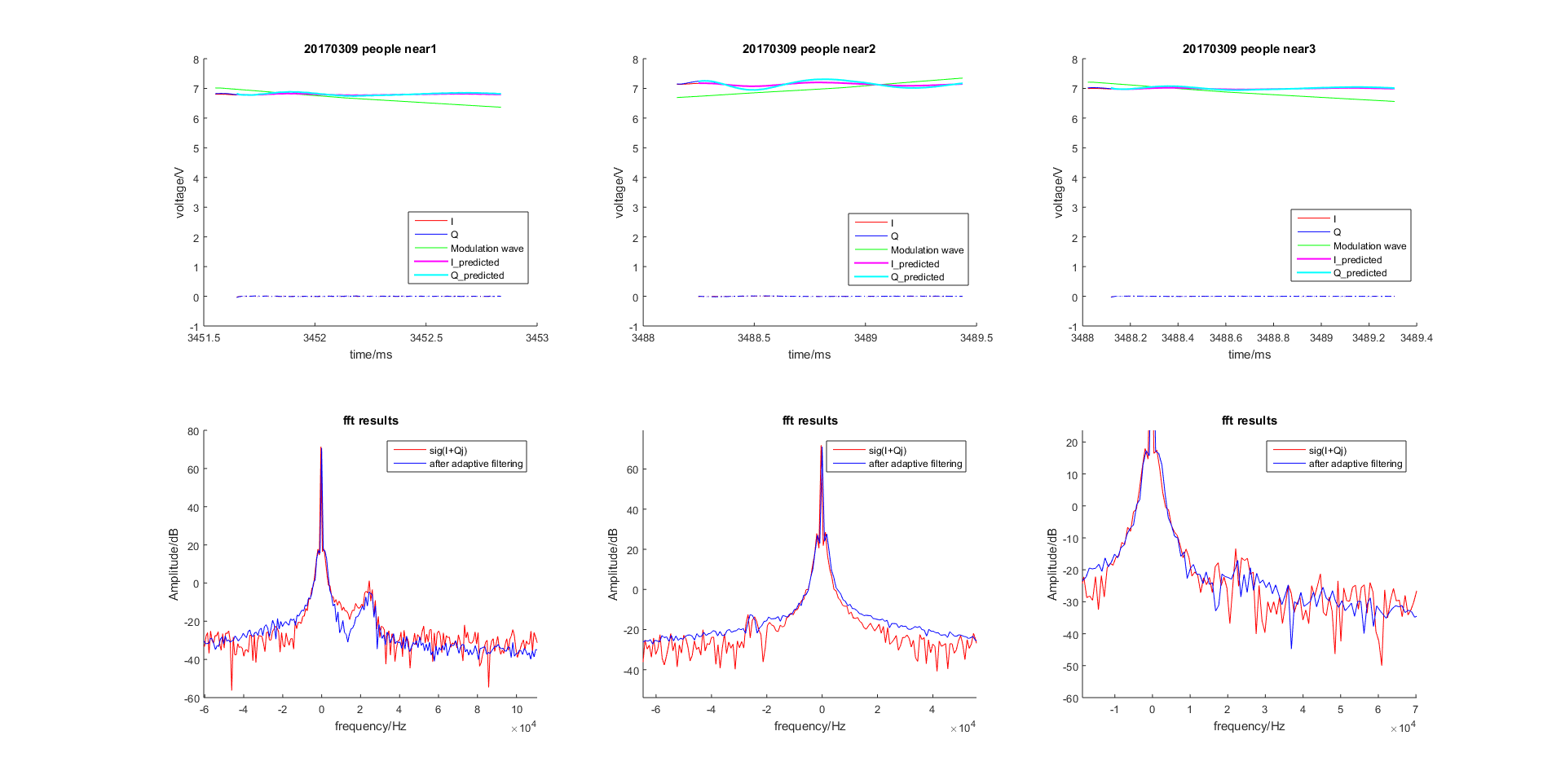
图 2.48 基于Normalized LMS的自适应滤波器滤波效果（参考信号为调制信号）

权重计算方法

  1. 正弦信号

  • 实验中, 以正弦信号为原始干净信号, 幅度为 A = 2, 频率为 f_s = 200Hz；

  • 噪声信号为三角波信号, 频率为 f_n = 3e2;

  • 参考输入信号为噪声信号, 幅度为其两倍；

  • 实验了基于 LMS 和 Normalized LMS 的权重更新算法；

当滤波器阶数及步长因子分别取为 param.M = 1; param.mu = 0.0001; 时, 迭代更新过程结果图如下:

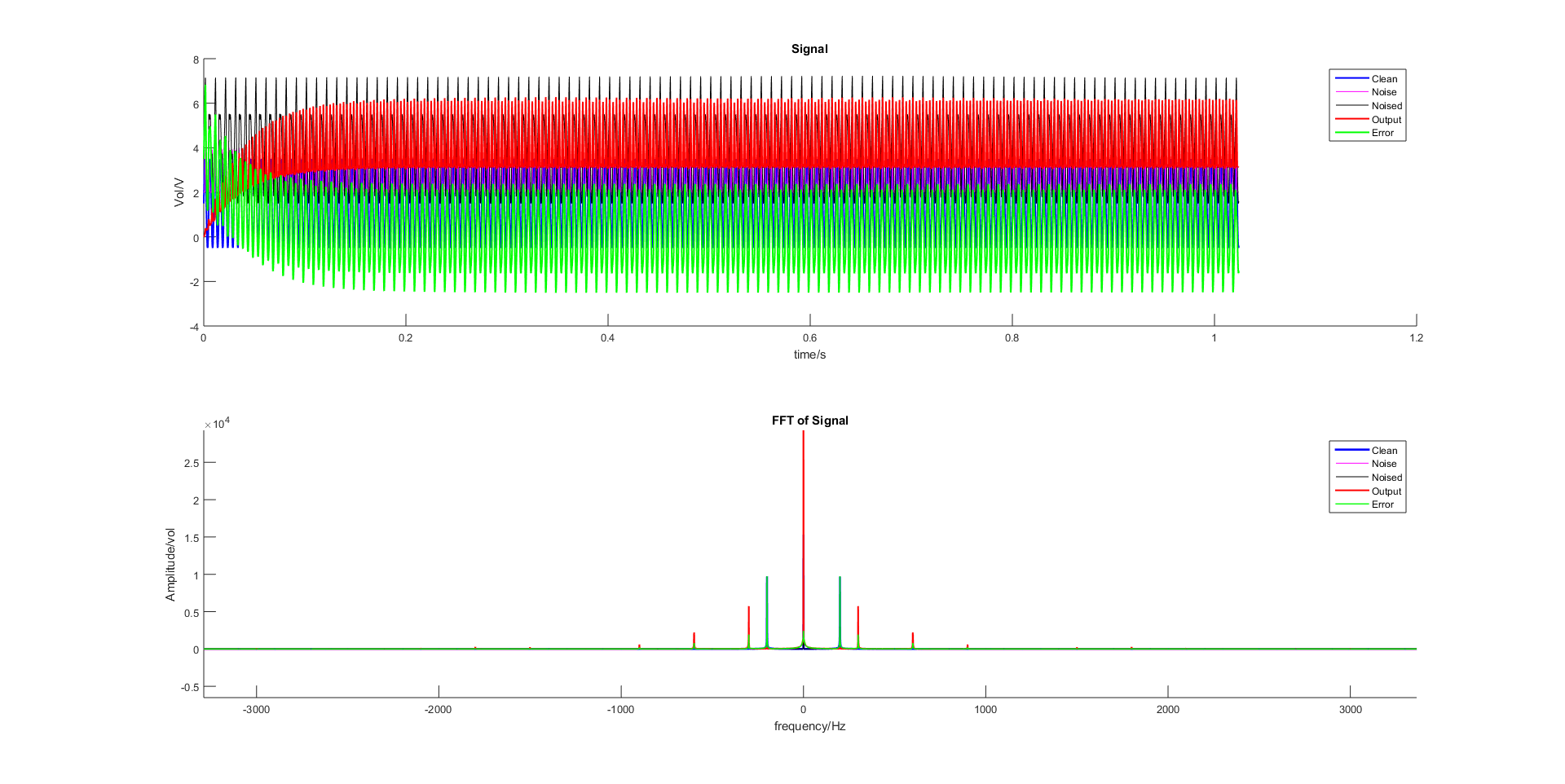
../../../_images/matlabDSP_LMS_itprocess_sin.png

图 2.49 基于LMS的自适应滤波器对带噪正弦信号的滤波效果（迭代过程图）

../../../_images/matlabDSP_NormLMS_itprocess_sin.png

图 2.50 基于Normalized LMS的自适应滤波器对带噪正弦信号的滤波效果（迭代过程图）

自适应滤波稳态后结果图如下:

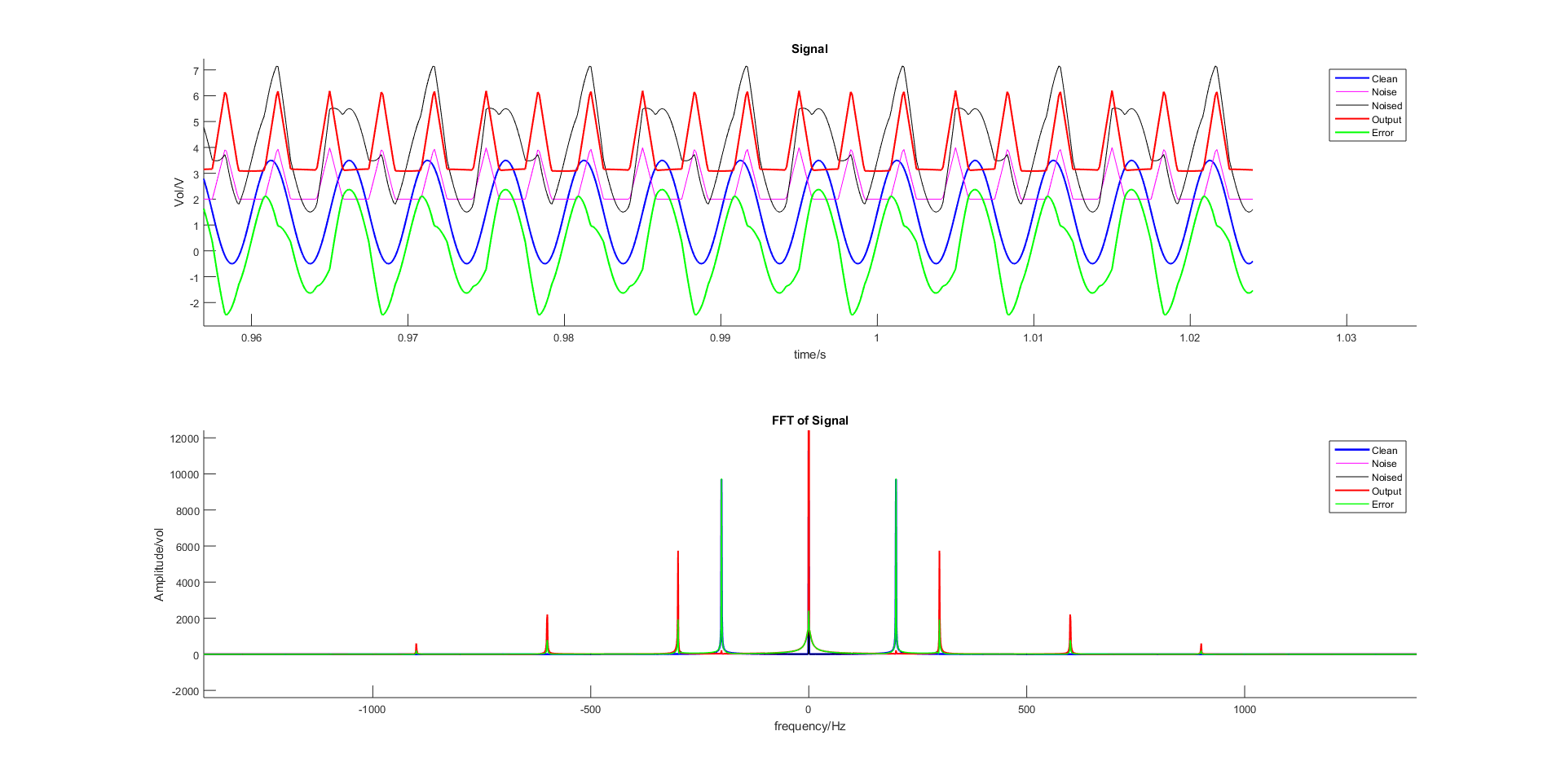
../../../_images/matlabDSP_LMS_stationary_sin.png

图 2.51 基于LMS的自适应滤波器对带噪正弦信号的滤波效果（稳态图）

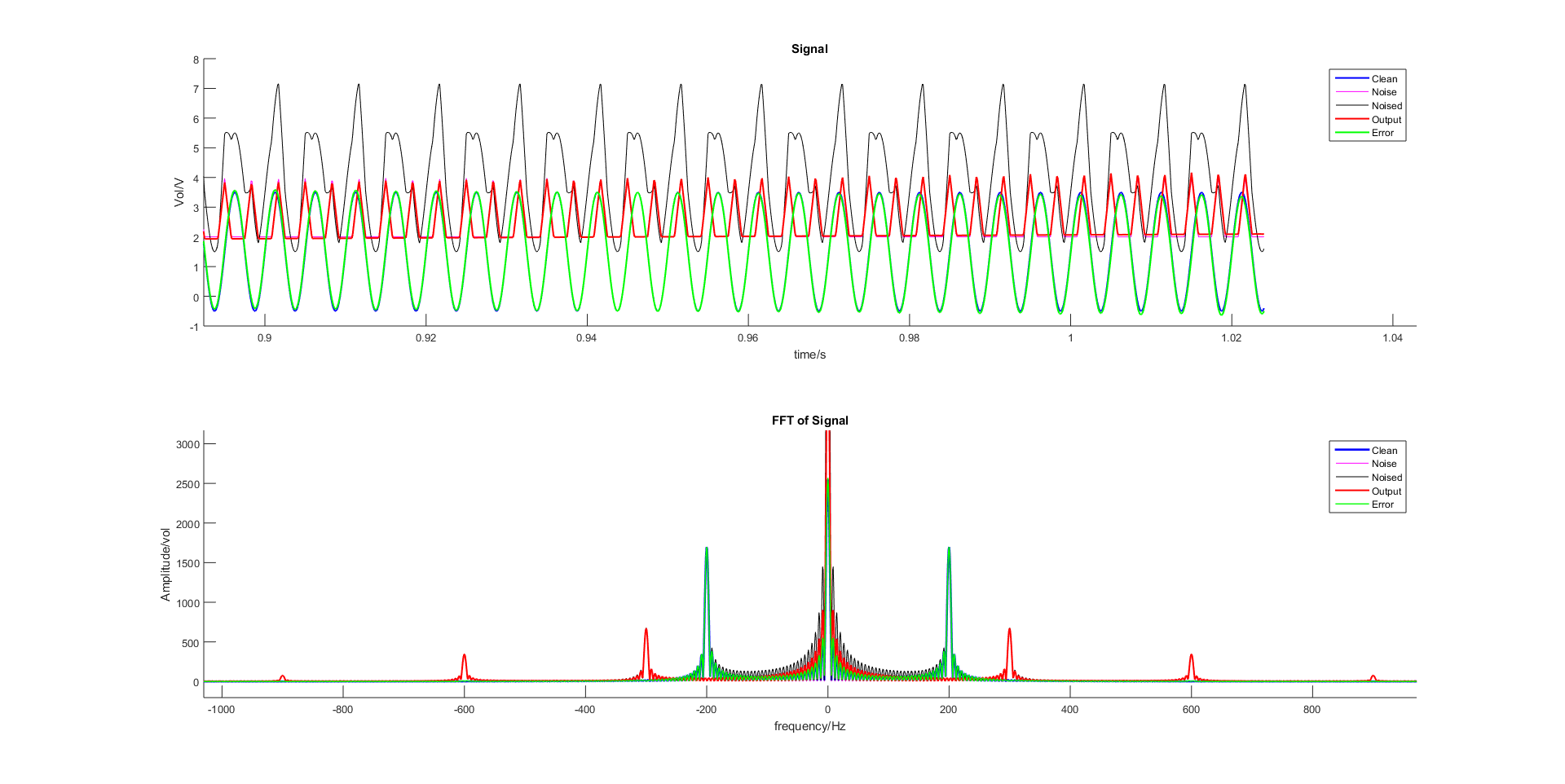
../../../_images/matlabDSP_NormLMS_stationary_sin.png

图 2.52 基于Normalized LMS的自适应滤波器对带噪正弦信号的滤波效果（稳态图）

  1. 雷达回波信号

对于雷达回波信号, 参考信号取为带噪宽带信号的时延信号, 效果图如下:

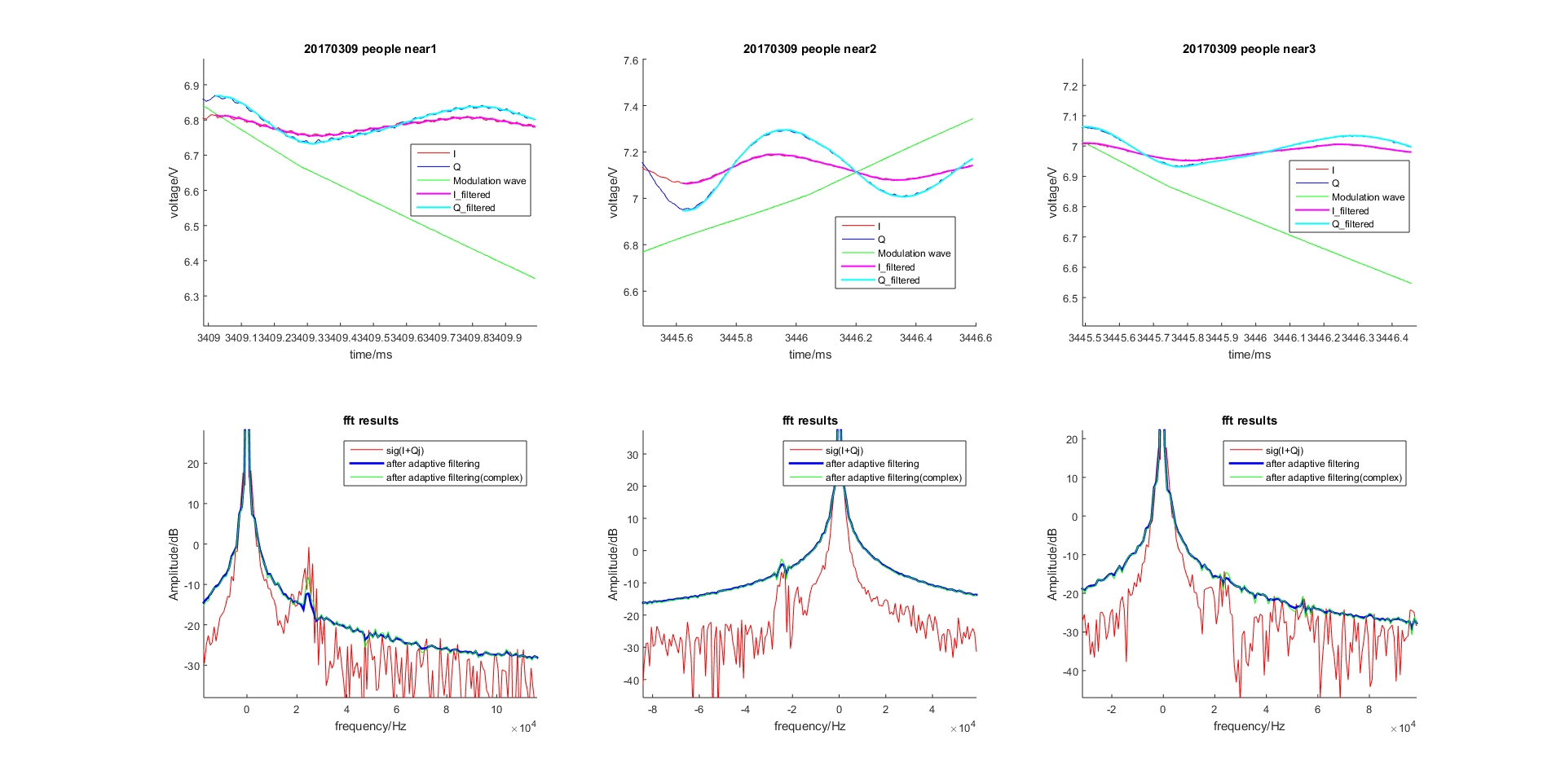
../../../_images/matlabDSP_LMS_stationary_radarecho.png

图 2.53 基于LMS的自适应滤波器对雷达回波宽带信号的滤波效果（稳态图）

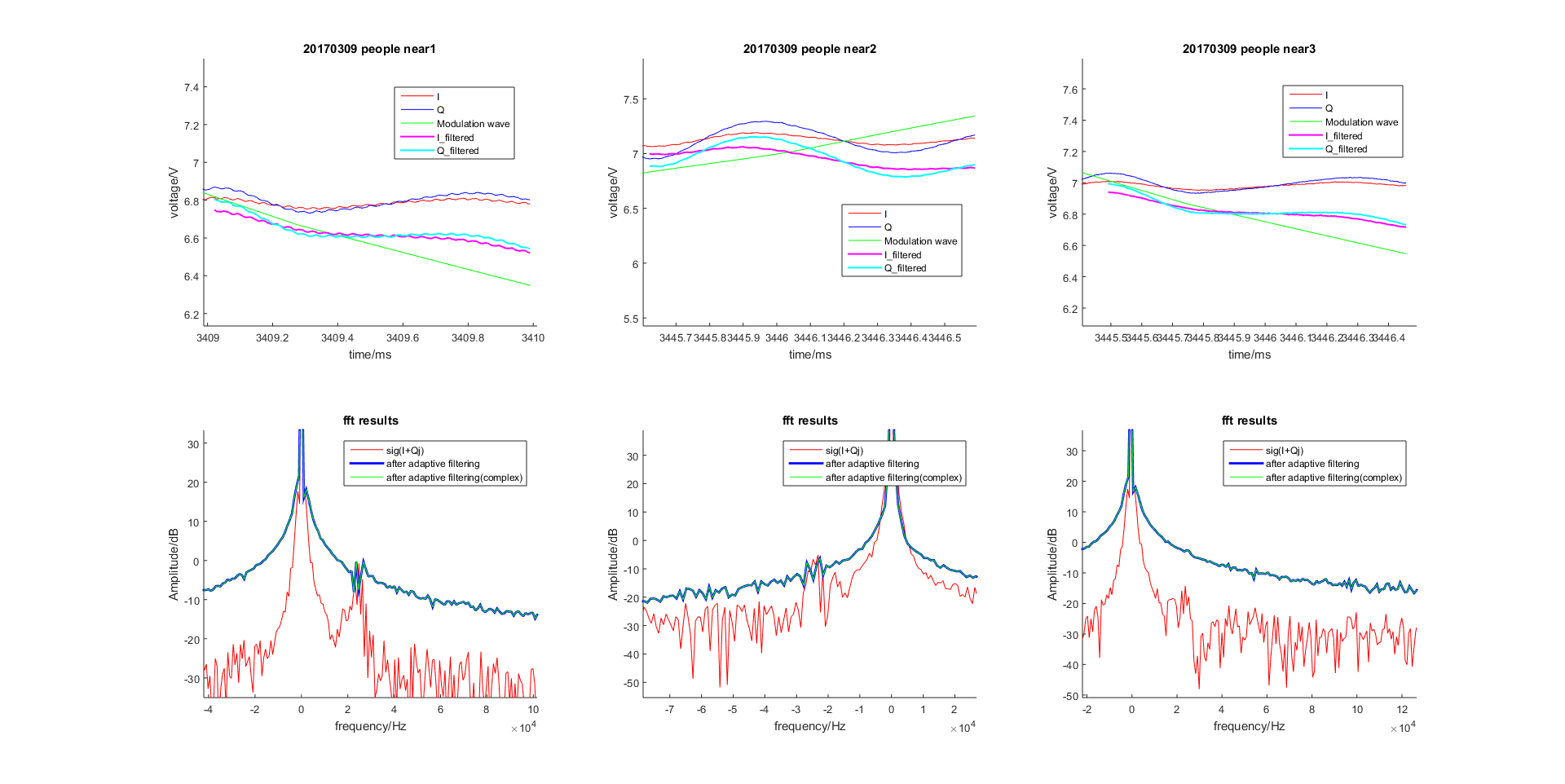
../../../_images/matlabDSP_NormLMS_stationary_radarecho.png

图 2.54 基于Normalized LMS的自适应滤波器对雷达回波宽带信号的滤波效果（稳态图）

滤波器阶数

  • 三角波调制信号重复频率为 1/4e-3 = 250Hz;

  • 参考输入信号: 带噪雷达回波时延信号；

  • 权重更新算法: LMS ；

  • 步长: param.mu = 0.0001 .

  1. 当滤波器阶数取为 param.M = 1 时

自适应滤波结果如图所示:

../../../_images/byme_LMS_radarecho_m1_stationary.png

图 2.55 滤波器阶数取为 1

  1. 当滤波器阶数取为 param.M = 10 时

自适应滤波结果如图所示:

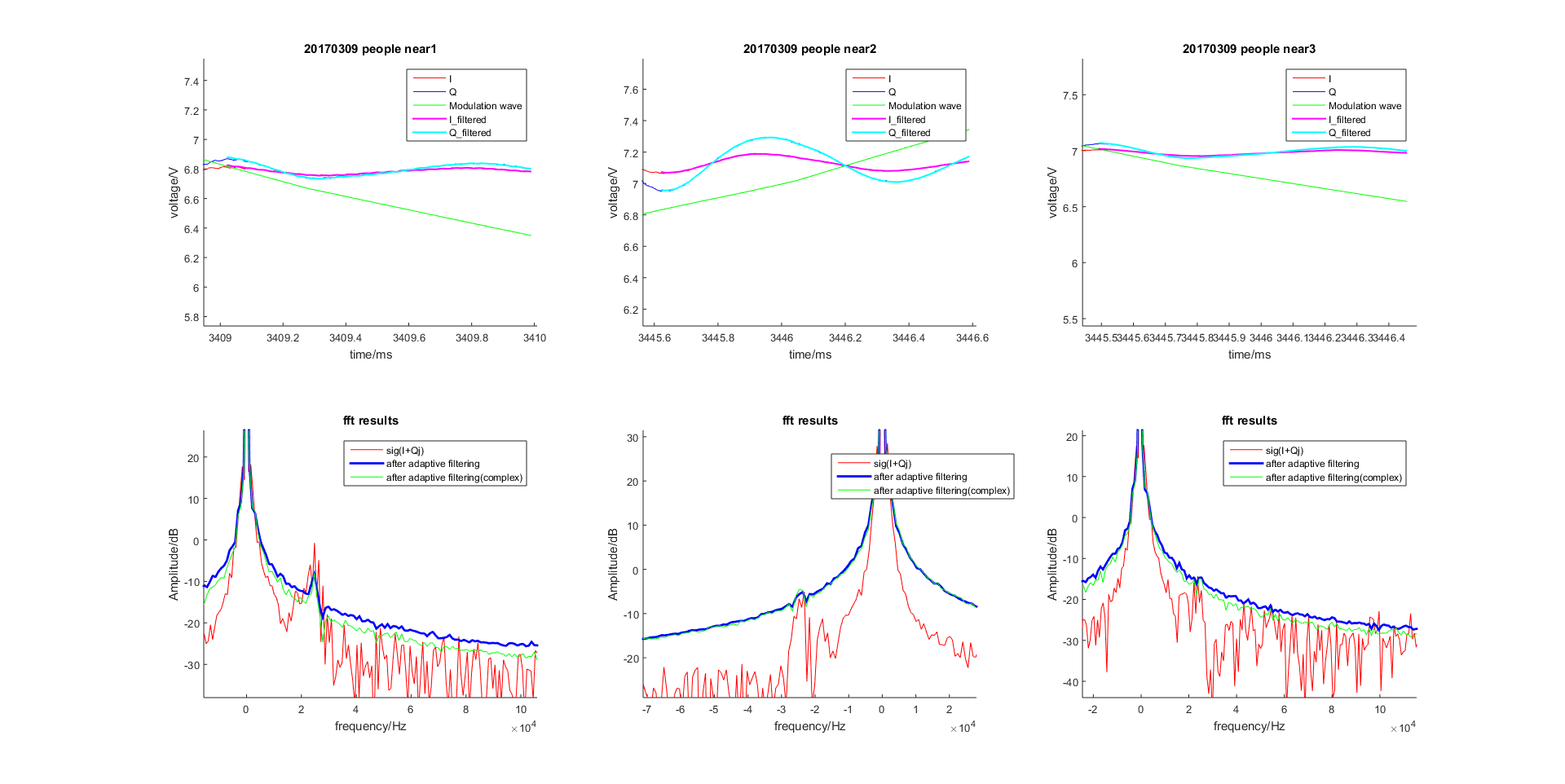
../../../_images/byme_LMS_radarecho_m10_stationary.png

图 2.56 滤波器阶数取为 10

  1. 当滤波器阶数取为 param.M = 30 时

自适应滤波结果如图所示:

../../../_images/byme_LMS_radarecho_m30_stationary.png

图 2.57 滤波器阶数取为 30

  1. 当滤波器阶数取为 param.M = 50 时

自适应滤波结果如图所示:

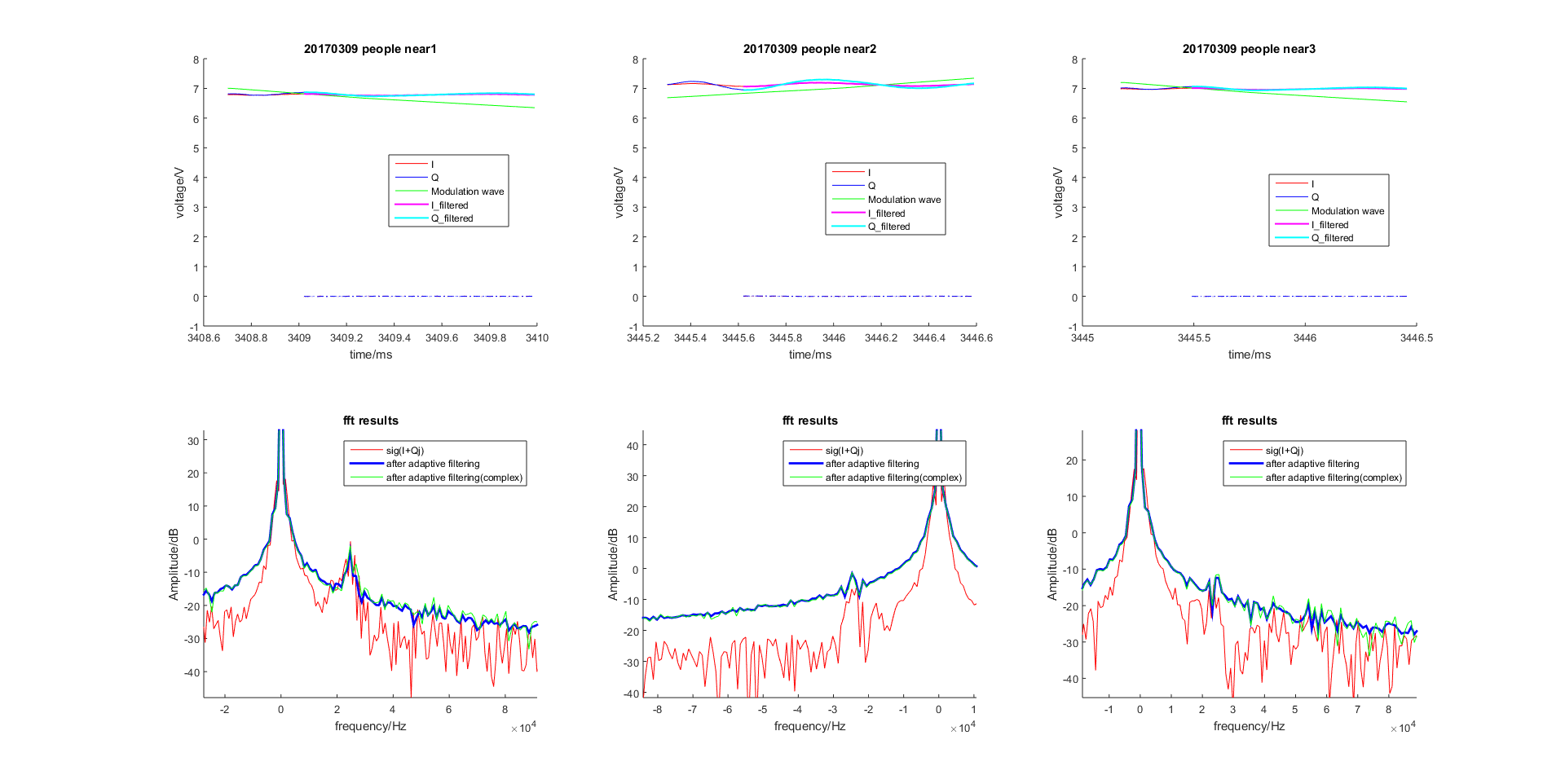
../../../_images/byme_LMS_radarecho_m50_stationary.png

图 2.58 滤波器阶数取为 50

步长因子

  • 三角波调制信号重复频率为 1/4e-3 = 250Hz;

  • 参考输入信号: 带噪雷达回波时延信号；

  • 权重更新算法: LMS ；

  • 滤波器阶数取为: param.M = 30 .

  1. 当步长因子为 param.mu = 0.001 时

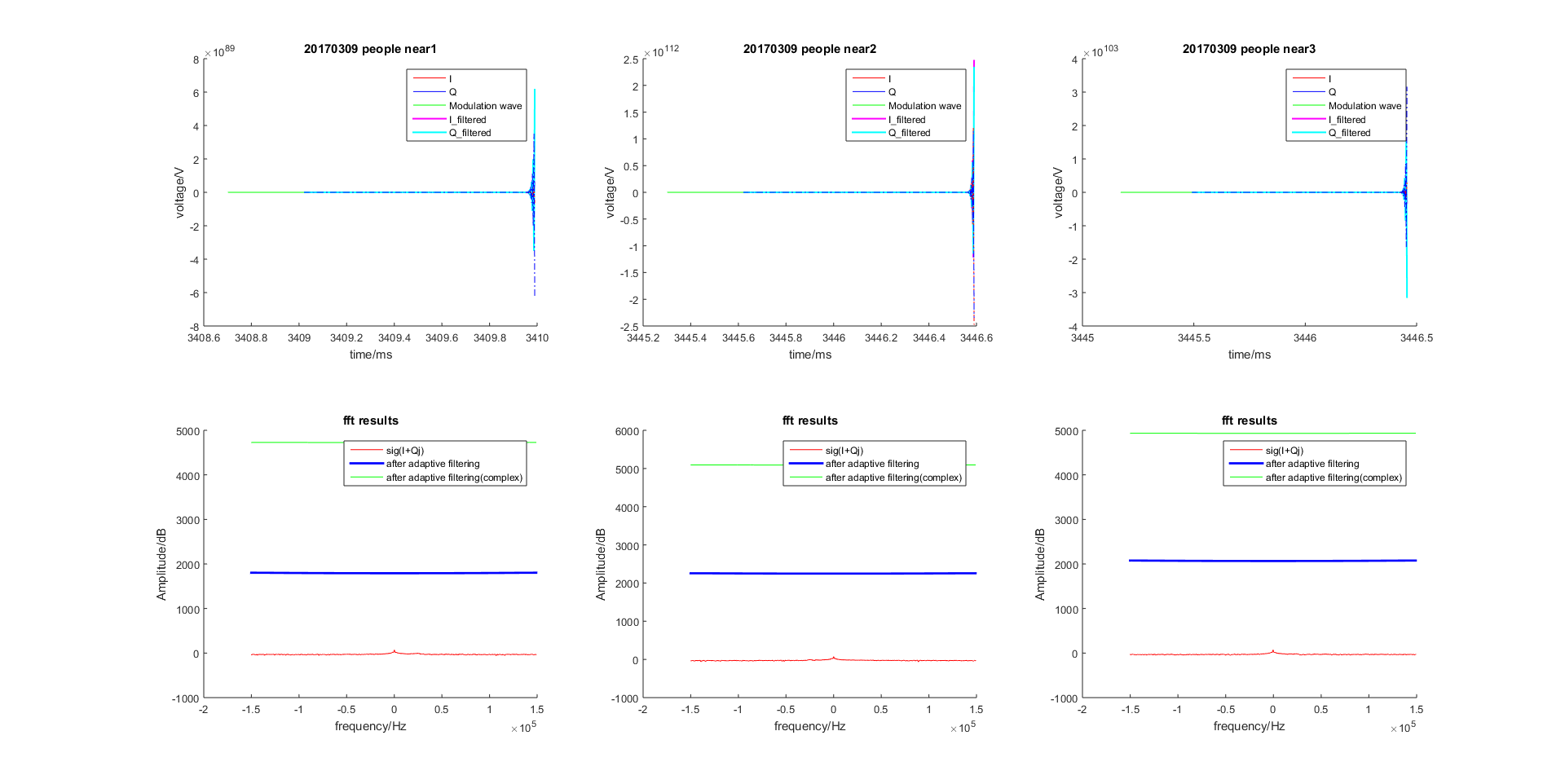
../../../_images/byme_LMS_radarecho_m30_mu1e-3_stationary.png

图 2.59 步长因子为 0.001

  1. 当步长因子为 param.mu = 0.0001 时

../../../_images/byme_LMS_radarecho_m30_mu1e-4_stationary.png

图 2.60 步长因子为 0.0001

  1. 当步长因子为 param.mu = 0.0003 时

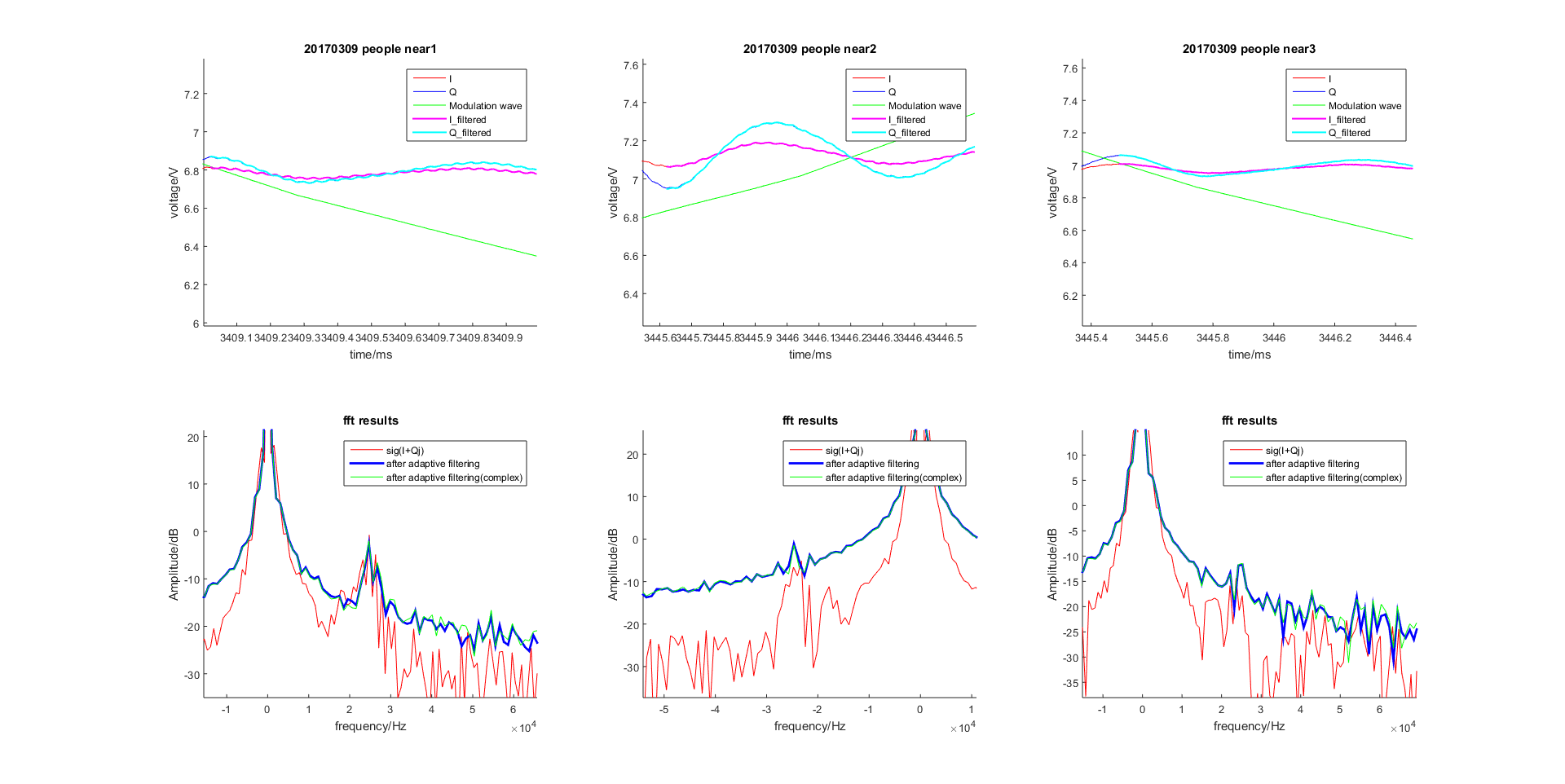
../../../_images/byme_LMS_radarecho_m30_mu3e-4_stationary.png

图 2.61 步长因子为 0.0003

  1. 当步长因子为 param.mu = 0.00001 时

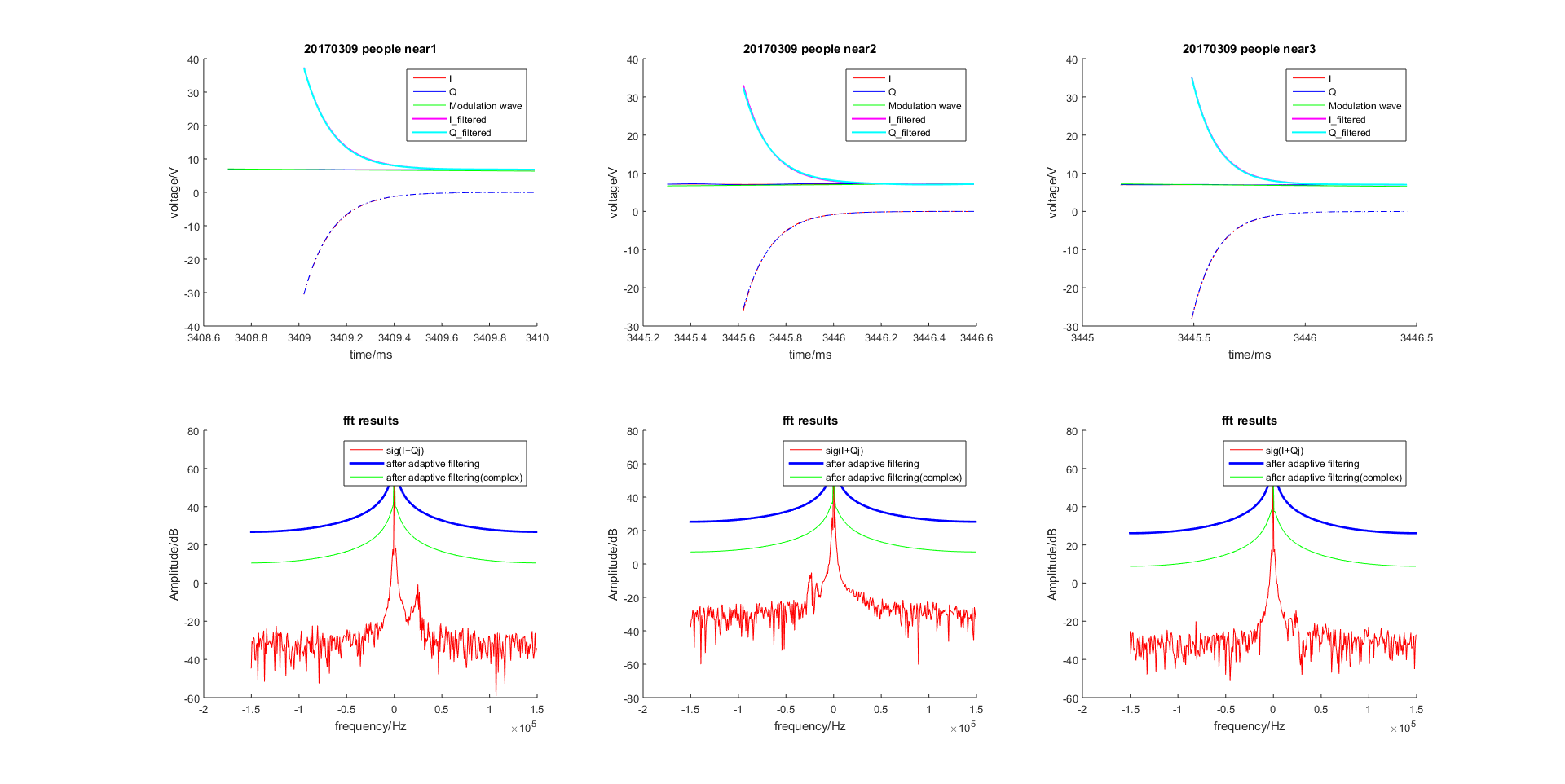
../../../_images/byme_LMS_radarecho_m30_mu1e-5_stationary.png

图 2.62 步长因子为 0.00001

结论: 步长越大, 收敛越快, 但若步长过大, 会导致很大误差！

2.1.3. 如何使用学习好的权重

利用学习好的权重滤波

核心代码:

LEN = length(input);
w = param.w;
M = param.M;
u = param.mu;

output = zeros(LEN,1);
err = output;

for k = M:LEN
    output(k) = input(k-M+1:k)'*w;
    err(k) = desired(k) - output(k);
end

效果如下:

../../../_images/usingweight_predict.png

图 2.63 直接利用学习好的权重滤波

基于学习好的权重再滤波

核心代码:

LEN = length(input);
w = param.w;
M = param.M;
u = param.mu;

output = zeros(LEN,1);
err = output;

for k = M:LEN
    output(k) = input(k-M+1:k)'*w;
    err(k) = desired(k) - output(k);
    w = w + 2*u*err(k).*input(k-M+1:k);          % update
end
../../../_images/usingweight_lmsfiltcontinue.png

图 2.64 使用学习好的权重初始化自适应滤波器