8.1. 经典卷积神经网络¶

卷积神经网络 (Convolutional Neural Network) [2] , 图像超分辨 [3]

8.1.1. 卷积神经网络举例¶

LeNet¶

Lecun等人于1998年提出 LeNet [2] , 网络结构如图 8.1 所示

图 8.1 LeNet结构.¶

LeNet结构.

AlexNet¶

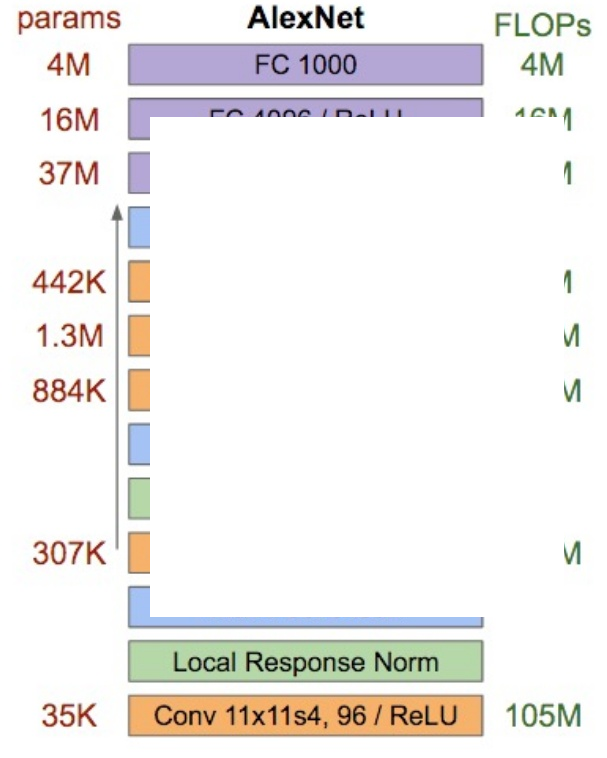
Alex等人于2012年提出 AlexNet [4] , 网络结构如图 8.2 所示

图 8.2 AlexNet结构.¶

AlexNet结构.

在AlexNet中, 使用了以下改进操作:

使用 \(\rm ReLU\) 作为激活函数, 并验证在较深的网络超过了 \(\rm Sigmoid\) , 成功解决了 \(\rm Sigmoid\) 在网络较深时的梯度弥散问题.
训练时使用Dropout正则方法, 以避免模型过拟合. Dropout虽有单独的论文论述, 但是AlexNet将其实用化, 通过实践证实了它的效果, 在AlexNet中主要是最后几个全连接层使用了Dropout.
使用重叠的最大池化, 此前CNN中普遍使用平均池化, AlexNet全部使用最大池化, 避免平均池化的模糊化效果. 并且AlexNet中提出步长尺寸要比池化核的尺寸小, 这样池化层的输出之间会有重叠和覆盖, 提升了特征的丰富性.
提出局部响应归一化单元, 模拟大脑中神经元的侧抑制现象.

在特定的几层经过 \(\rm ReLU\) 非线性激活函数后, 使用了局部响应归一化 (Local Response Normalization, LRN) 单元:

(8.1)¶\[b_{x, y}^{i}=a_{x, y}^{i} / \left( \begin{array}{c}{\min (N-1, i+n / 2)} \\ k+\alpha{ \sum_{j=\max (0, i-n / 2)}^{i}\left(a_{x, y}^{j}\right)^{2}}\end{array}\right)^{\beta} \]

其中, \(N\) 为当前层中卷积核的个数, \(k, n, \alpha, \beta\) 为超参数, 并使用验证集来确定其值, 文中取值为 \(k=2, n=5, \alpha=10^{-4}, \beta=0.75\) , LRN 模拟了大脑中的侧抑制现象, 对局部神经元进行激励与抑制, 使得其中响应比较大的神经元响应值变得更大, 并抑制其他响应较小的神经元, 增强了模型的泛化能力.

tensorflow下, 主要实现代码:

VGGNet¶

[5]

GoogleNet¶

[6]