3.1. 回波信号模型

3.1.1. SAR回波信号

目标回波分析

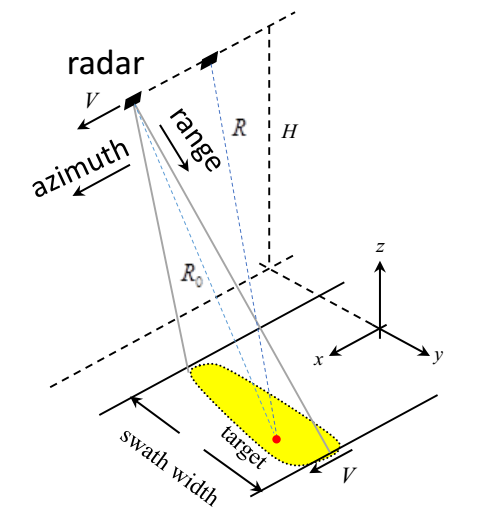
点目标成像

由图中几何关系知: \(R(\eta)^2 = R_0^2 + (V\eta)^2\) , 在低斜视角下, \(R(\eta)\) 可由菲涅尔近似为: \(R(\eta) = R_0 + \frac{(V\eta)^2}{2R_0}\)

接收的回波信号为二维的线性调频信号, 点目标回波表达式为:

\[\begin{array}{l} {s_r}(\tau ,\eta ) = {A_0}{w_r}(\tau - 2R(\eta )/C){w_a}(\eta - {\eta}_c)\\ \exp \left( {2\pi {f_0}(\tau - 2R(\eta )/C) + \pi {K_r}{{(\tau - 2R(\eta )/C)}^2}} \right) \end{array} \]

去除载频后的基带信号为:

\[\begin{array}{l} {s_r}(\tau ,\eta ) = {A_0}{w_r}(\tau - 2R(\eta )/C){w_a}(\eta - {\eta}_c)\\ \exp \left( {-j4\pi {f_0}R(\eta )/C + j\pi {K_r}{{(\tau - 2R(\eta )/C)}^2}} \right) \end{array} \]

其中:

  • \(A_0\) 为复数, 代表点目标的后向散射引起的一个相位和幅度变化, \(A_0={A^\prime}_0 \exp \left(j\phi\right)\) , \({A^\prime}_0\) 为后向散射系数, \(\phi\) 为地表散射引起的雷达信号相位的改变

  • \(\tau\) 为距离向时间

  • \(\eta\) 为方位向时间, \(\eta_c\) 为零多普勒时间

  • \(w_a(\cdot)\) 为方位向天线增益, \(w_r(\cdot)\) 为距离向天线增益

  • \(f_0\) 为载频

通常取全向天线增益为1, 则回波变为:

\[\begin{array}{l} {s_r}(\tau ,\eta ) = {A_0} \exp \left( {-j4\pi {f_0}R(\eta )/C + j\pi {K_r}{{(\tau - 2R(\eta )/C)}^2}} \right) \end{array} \]

二维场景离散化：

\[\begin{array}{lll} s({t_{a,{n_a}}},{t_{r,{n_r}}}) = \sum\limits_{i = 1}^H {\sum\limits_{j = 1}^W {g(i,j) \cdot p\left( {{t_{r,{n_r}}} - 2R({t_{a,{n_a}}},i,j)/c} \right)} }\exp \left( { - j4\pi {f_c}R({t_{a,{n_a}}},i,j)/c} \right), \end{array} \]

目标回波基础理论

SAR的回波数据可以看作是地面反射率 \(\gamma(\tau, \eta)\) 与雷达系统冲激响应 \(h(\tau, \eta)\) 进行二维卷积, 即:

\[S(\tau, \eta)=\gamma(\tau, \eta) \otimes h(\tau, \eta) + n(\tau, \eta) \]

其中, \(n(\tau, \eta)\) 为系统噪声. 因此不管是点目标还是面目标都可以通过SAR的接收信号的一般模型求得回 波表达式, SAR 的成像处理过程, 其实际上也是一个通过解卷积从回波信号中最 大程度地、无失真地提取地表的后向散射系数的二维分布

3.1.2. 时域回波仿真

在得到点目标回波信号后, 传统的时域回波模拟方法也叫距离时域脉冲相干 算法是将一个目标场景图像细化成一个点阵, 直接模拟雷达的工作过程,在雷达平台方位向的每一个位置,先计算出天线波束照射范围内即距离向每个点目标的回波信号,然后将这些信号叠加得到最终的回波信号.

点目标

单个点目标回波的表达式即为上述点目标回波表达式, 多个点目标可以看成每个点目标回波的叠加:

\[s(\tau, \eta) = \sum_{i=1}^{n}{s_i(\tau,\eta)} \]

其中, \(n\) 为点目标的个数, \(s_i(\tau,\eta)\) 为点目标回波.

面目标

对于面目标就是把目标场景分割成一个均匀分布的点阵. 这个是相对精确地面目标时域回波仿真方法, 但是在面目标相对较大时, 那么它被分割成的点 阵数量就多, 相应的数据量就大, 计算量也高.