1.2. 凸多边形区域填充

1.2.1. 问题分析

1.2.2. 填充算法

扫描线法

夹角和法

内部点与各顶点夹角和为360度.

多边形方程法

该方法的核心思想是 多边形内的点满足多边形区域的边构成的不等式方程组, 设有由 \(N\) 个有序顶点 \({\mathbb P}=\{(x_i, y_i)^T\}_{i=1}^N\) 按顺序(逆时针或顺时针)构成的多边形区域 \(\mathcal P\).

若按逆时针方向, 则多边形内的区域可以表示为不等式方程组

(1.9)\[\begin{aligned} l_1 &: a_1 x + b_1 y + c_1 \geq 0\\ l_2 &: a_2 x + b_2 y + c_2 \geq 0\\ & {\ \vdots} \\ l_{N} &: a_{N} x + b_{N} y + c_{N} \geq 0 \end{aligned}. \]

若按顺时针方向, 则多边形内的区域可以表示为不等式方程组

(1.10)\[\begin{aligned} l_1 &: a_1 x + b_1 y + c_1 \leq 0\\ l_2 &: a_2 x + b_2 y + c_2 \leq 0\\ & {\ \vdots} \\ l_{N} &: a_{N} x + b_{N} y + c_{N} \leq 0 \end{aligned}. \]

其中, \(a_n = y_n-y_{n+1}\), \(b_n = x_{n+1}-x_{n}\), \(c_{n} = y_{n+1}(x_{n}-x_{n+1})-x_{n+1}(y_{n}-y_{n+1})\), \(n=1,2,\cdots, N\), 且 \(x_{N+1} = x_{1}, y_{N+1} = y_{1}\).

综上可知, 凸多边形区域内的点对应的凸多边形不等式方程组中的不等式同号.

故若要判断一点 \(P_0=(x_0, y_0)^T\) 是否在某凸多边形区域内, 只需要将改点坐标代入 式.1.11, 判断是否同号即可. 若满足则待填充点在多边形区域内, 反之不在.

(1.11)\[\begin{aligned} l_1 &: a_1 x + b_1 y + c_1 \\ l_2 &: a_2 x + b_2 y + c_2 \\ & {\ \vdots} \\ l_{N} &: a_{N} x + b_{N} y + c_{N} \end{aligned}. \]

1.2.3. 实验与分析

实验1

实验设置

假如对由有序顶点集合 \(\{(0, 0), (200, 0), (200, 100), (0, 100)\}\) 确定的方形区域 \(\mathcal R\) 内的凸多边形区域 \(\mathcal P\) 进行区域填充, 其中, \(\mathcal P\) 由有序顶点集合 \(\{(50, 50), (40, 40), (42, 25)\), \((55, 5), (65, 20), (70, 40), (60, 50)\}\) 确定. 记水平与垂直方向上的离散化尺度分别为 \(d_x, d_y\), 分析对比不同尺度下, 各种凸多边形填充算法的执行效率与填充效果.

实验代码

实验中用到的代码可在 这里 和 这里 下载, 主程序代码见 代码 1.6

代码 1.6 demo_ConvexPolygonFilling.m
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
clear all
close all
clc

H = 100;
W = 200;
% dy = 0.1;
% dx = 0.1;
% dy = 0.5;
% dx = 0.5;
dy = 1;
dx = 1;

Polygon = [50 50; 40 40; 42 25; 55 5; 65 20; 70 40; 60 50]; % Anti Clockwise
% Polygon = [60 50; 70 40; 65 20; 55 5; 42 25; 40 40; 50 50]; % Clockwise
% Polygon = [50 50; 40 40; 55 5; 70 40; 58 42];

[y, x] = meshgrid(1:dy:H, 1:dx:W);
y = y(:);
x = x(:);
Points = [x y];

tic;
s1 = isincvxplg(Points, Polygon, 'Angle');
toc;

tic;
s2 = isincvxplg(Points, Polygon, 'PolygonEquations');
toc;

figure
hold on
subplot(121)
cpplot(Polygon, '-r', 'linewidth', 2)
opplot(Points(s1, :), '*r', 'linewidth', 1)

subplot(122)
cpplot(Polygon, '-r', 'linewidth', 2)
opplot(Points(s2, :), '*r', 'linewidth', 1)

凸多边形区域填充算法核心代码如 代码 1.7 所示:

代码 1.7 isincvxplg.m
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
function [ s ] = isincvxplg( Points, Polygon, Method )
%ISINCVXPLG judges whether a point is in a convex polygon area
%
% s = ISINCVXPLG( Points, Polygon ) returns the the status (in Polygon --> 1,
%   not in Polygon --> 0) of each point in Points.
%
% s = ISINCVXPLG( Points, Polygon, Method ) returns the the status (in Polygon --> 1,
%   not in Polygon --> 0) of each point in Points using method 'Method'.
%   Points: N-2 array, [x y;x y;...]
%   Polygon: L-2 array, [x y;x y;...]
%   Method: 'Angle' (default), 'PolygonEquations'
%
%   Examples
%   --------
%
%   Points = [1 1; 2 2;3 3];
%   Polygon = [1 2;1.5 1;2.5 1;3 2;2 3];
%   cpplot(Polygon, '-r', 'linewidth', 2)
%   hold on
%   opplot(Points, '*r', 'linewidth', 1)
%   s = isinpolygon(Points, Polygon)
%   s =
%
%       0
%       1
%       0
%   s = isinpolygon(Points, Polygon, 'PolygonEquations')
%
%
%   See also isincircle.
%
%   Copyright 2019-2030 Zhi Liu, https://iridescent.ink/.
%

if nargin < 3
    Method = 'Angle';
end
EPS = 1e-6;
nPoints = size(Points, 1);
nVertex = size(Polygon, 1);
PI2 = pi + pi;
Polygon = Polygon(:, 1:2);
s = false(nPoints, 1);

if strcmp(Method, 'Angle')
    for n = 1:nPoints
        Pg = bsxfun(@minus, Polygon, Points(n, :));
        Pa = Pg(1:nVertex, :);
        Pb = [Pg(2:nVertex, :); Pg(1, :)];
        A = angle2(Pa, Pb, 0);
        A = abs(A);
        sumA = sum(A, 1);
        if abs(sumA - PI2) < EPS
            s(n) = 1;
        else
            s(n) = 0;
        end
    end
end

if strcmp(Method, 'PolygonEquations')
    Q = mean(Polygon, 1);
    Ls = zeros(nVertex, 4); % edges
    for nv = 1:nVertex-1
        Ls(nv, :) = [Polygon(nv, :), Polygon(nv+1, :)];
    end
    Ls(end, :) = [Polygon(end, :), Polygon(1, :)];

    A = Ls(:, 2) - Ls(:, 4);
    B = Ls(:, 3) - Ls(:, 1);
    C = Ls(:, 4) .* (Ls(:, 1) - Ls(:, 3)) - Ls(:, 3) .* (Ls(:, 2) - Ls(:, 4));

    for n = 1:nPoints
        fp = A * Points(n, 1) + B * Points(n, 2) + C;
        s(n) = (sum((fp >= 0))== nVertex) || (sum((fp > 0)) == 0);
    end
end

end

实验结果

我们在MatlabR2019上实现上述算法, 硬件平台为Intel® Xeon(R) CPU E5-2696 v3 @ 2.30GHz × 36, 实验中仅使用单线程, 运行时间如 表 1.1 所示, 填充效果如 图 1.12 所示. 对比表格与填充效果图可知, 多边形方程法计算复杂度更低, 耗时极短, 效率更高.

表 1.1 不同填充算法耗时对比

方法

\(d_x=d_y=1\)

\(d_x=d_y=0.5\)

\(d_x=d_y=0.1\)

夹角和法

0.758408s

2.397315s

57.775898s

多边形方程法

0.020063s

0.056518s

0.943451s
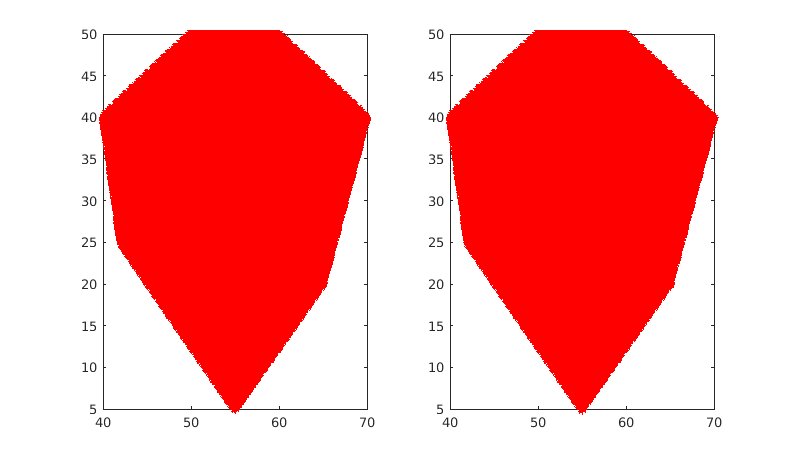
凸多边形区域填充方法示例

图 1.12 凸多边形区域填充结果对比图. 夹角和法(左), 多边形方程法(右)