torchcs.sensing package

Submodules

torchcs.sensing.bernoullis module

torchcs.sensing.bernoullis.bernoulli(shape, seed=None, norm=True, rmmean=False, dtype='float32', device='cpu')

generates Bernoulli observation matrix

Generates M-by-N Bernoulli observation matrix which have Bernoulli distribution elements( columns are l2 normalized).

Parameters

  • shape (list or tuple) – shape of Gauss observation matrix [M, N]

  • seed (int or None, optional) – the seed for random number generator, by default None

  • norm (bool, optional) – normalize the columns of observation matrix, by default True

  • rmmean (bool, optional) – remove the mean values before normalization, by default False

  • dtype (str, optional) – torch’s data type, such as 'float32', 'float64', 'complex64', 'complex128', by default 'float32'

  • device (str, optional) – generates data on the specified device, supported are 'cpu', 'cuda:x', where, x is the cuda device’s id.

Returns

Bernoulli observation matrix \(\bm A\).

Return type

th.Tensor

Examples

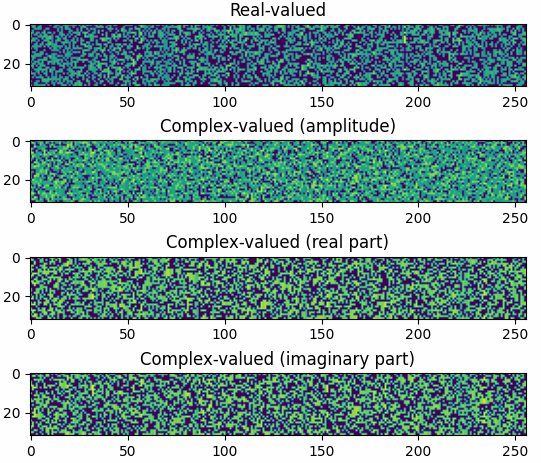
_images/BernoulliMatrix.png

The results shown in the above figure can be obtained by the following codes.

import torchcs as tc
import matplotlib.pyplot as plt

PhiReal = tc.bernoulli((32, 256), dtype='float32')
PhiCplx = tc.bernoulli((32, 256), dtype='complex64')
print(PhiReal.shape)
print(PhiCplx.shape)

plt.figure()
plt.subplot(411)
plt.imshow(PhiReal)
plt.title('Real-valued')
plt.subplot(412)
plt.imshow(PhiCplx.abs())
plt.title('Complex-valued (amplitude)')
plt.subplot(413)
plt.imshow(PhiCplx.real)
plt.title('Complex-valued (real part)')
plt.subplot(414)
plt.imshow(PhiCplx.imag)
plt.title('Complex-valued (imaginary part)')
plt.show()

torchcs.sensing.binary module

torchcs.sensing.binary.brandom(shape, dtype='float32', device='cpu')

generates binary-random subsampling matrix

Generates M-by-N binary-random observation matrix which have uniform distribution elements.

Parameters

  • shape (list or tuple) – shape of Gauss observation matrix [M, N]

  • dtype (str, optional) – torch’s data type, such as 'float32', 'bool', by default 'float32'

  • device (str, optional) – generates data on the specified device, supported are 'cpu', 'cuda:x', where, x is the cuda device’s id.

Returns

binary-random subsampling observation matrix \(\bm A\).

Return type

th.Tensor

Examples

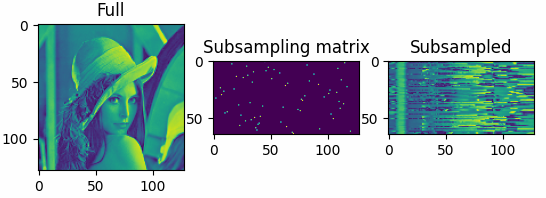
_images/BrandomMatrix.png

The results shown in the above figure can be obtained by the following codes.

import torchbox as tb

imgfile = tb.data_path('optical') + 'LenaGRAY128.png'
X = tb.imread(imgfile)* 1.

Phi = tb.brandom(shape=(64, 128))
print(Phi.shape)

Y = Phi @ X

plt = tb.imshow([X, Phi, Y], titles=['Full', 'Subsampling matrix', 'Subsampled'])
plt.show()
torchcs.sensing.binary.buniform(shape, dtype='float32', device='cpu')

generates binary-uniform subsampling matrix

Generates M-by-N binary-uniform observation matrix.

Parameters

  • shape (list or tuple) – shape of Gauss observation matrix [M, N]

  • dtype (str, optional) – torch’s data type, such as 'float32', 'bool', by default 'float32'

  • device (str, optional) – generates data on the specified device, supported are 'cpu', 'cuda:x', where, x is the cuda device’s id.

Returns

binary-uniform subsampling observation matrix \(\bm A\).

Return type

th.Tensor

Examples

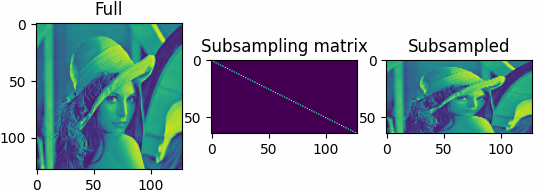
_images/BuniformMatrix.png

The results shown in the above figure can be obtained by the following codes.

import torchbox as tb

imgfile = tb.data_path('optical') + 'LenaGRAY128.png'
X = tb.imread(imgfile)* 1.

Phi = tb.buniform(shape=(64, 128))
print(Phi.shape)

Y = Phi @ X

plt = tb.imshow([X, Phi, Y], titles=['Full', 'Subsampling matrix', 'Subsampled'])
plt.show()

torchcs.sensing.gaussians module

torchcs.sensing.gaussians.gaussian(shape, seed=None, norm=True, rmmean=True, dtype='float32', device='cpu')

generates Gaussian observation matrix

Generates M-by-N Gaussian observation matrix which have gaussian distribution elements( columns are l2 normalized).

\[{\bm \Phi} \sim {\mathcal N}(0, \frac{1}{M}) \]
Parameters

  • shape (list or tuple) – shape of Gauss observation matrix [M, N]

  • seed (int or None, optional) – the seed of the random number generator, by default None

  • norm (bool, optional) – normalize the columns of observation matrix, by default True

  • rmmean (bool, optional) – remove the mean values before normalization, by default True

  • dtype (str, optional) – torch’s data type, such as 'float32', 'float64', 'complex64', 'complex128', by default 'float32'

  • device (str, optional) – generates data on the specified device, supported are 'cpu', 'cuda:x', where, x is the cuda device’s id.

Returns

Gauss observation matrix \(\bm A\).

Return type

th.Tensor

Examples

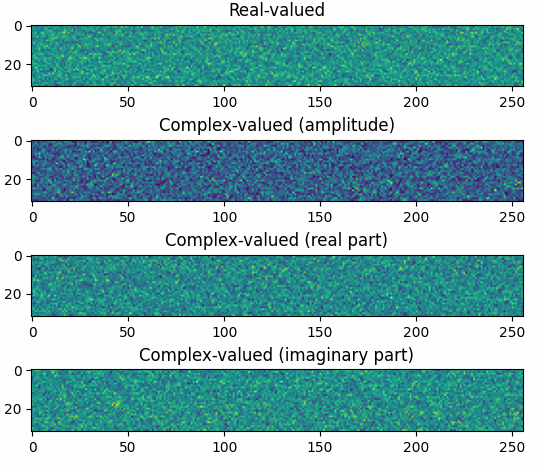
_images/GaussianMatrix.png

The results shown in the above figure can be obtained by the following codes.

import torchcs as tc
import matplotlib.pyplot as plt

PhiReal = tc.gaussian((32, 256), dtype='float32')
PhiCplx = tc.gaussian((32, 256), dtype='complex64')
print(PhiReal.shape)
print(PhiCplx.shape)

plt.figure()
plt.subplot(411)
plt.imshow(PhiReal)
plt.title('Real-valued')
plt.subplot(412)
plt.imshow(PhiCplx.abs())
plt.title('Complex-valued (amplitude)')
plt.subplot(413)
plt.imshow(PhiCplx.real)
plt.title('Complex-valued (real part)')
plt.subplot(414)
plt.imshow(PhiCplx.imag)
plt.title('Complex-valued (imaginary part)')
plt.show()

torchcs.sensing.toeplitz module

torchcs.sensing.toeplitz.toeplitz(shape, verbose=True)

generates Toeplitz observation matrix

Generates M-by-N Toeplitz observation matrix

\[{\bm \Phi}_{ij} = \left[\begin{array}{ccccc}{a_{0}} & {a_{-1}} & {a_{-2}} & {\cdots} & {a_{-n+1}} \\ {a_{1}} & {a_{0}} & {a_{-1}} & {\cdots} & {a_{-n+2}} \\ {a_{2}} & {a_{1}} & {a_{0}} & {\cdots} & {a_{-n+3}} \\ {\vdots} & {\vdots} & {\vdots} & {\ddots} & {\vdots} \\ {a_{n-1}} & {a_{n-2}} & {a_{n-3}} & {\cdots} & {a_{0}}\end{array}\right] \]
Parameters

shape (list or tuple) – shape of Toeplitz observation matrix [M, N]

Keyword Arguments

verbose (bool) – display log info (default: {True})

Returns

A – Toeplitz observation matrix \(\bm A\).

Return type

ndarray

Module contents