torchcs.recovery package

Submodules

torchcs.recovery.dlmlcs module

class torchcs.recovery.dlmlcs.Cnn1d(cin=1)

Bases: torch.nn.modules.module.Module

forward(x)

Defines the computation performed at every call.

Should be overridden by all subclasses.

Note

Although the recipe for forward pass needs to be defined within this function, one should call the Module instance afterwards instead of this since the former takes care of running the registered hooks while the latter silently ignores them.

training: bool
class torchcs.recovery.dlmlcs.CsNet1d(cin=1, lr=0.1, seed=None, device='cpu')

Bases: object

Neural network for compressed reconstruction

Parameters

  • cin (int, optional) – the number of channels of input signal, by default 1

  • lr (float, optional) – learning rate, by default 0.1

  • seed (int or None, optional) – random seed for weight initialization, by default None (not set)

  • device (str, optional) – computation device, 'cuda:x' or 'cpu' by default 'cpu'

load(modelfile)

load network model from a file

Parameters

modelfile (str) – model file path

save(modelfile)

save network model to a file

Parameters

modelfile (str) – model file path

test(Y, bs)
Parameters

  • Y (tensor) – input for testing, \(N\times C\times L\)

  • bs (int) – batch size

Returns

recovered signals

Return type

tensor

train(Ytrain, Xtrain, Yvalid, Xvalid, bs, nepoch)
Parameters

  • Ytrain (tensor) – input for training, \(N\times C\times L\)

  • Xtrain (tensor) – target for training

  • Yvalid (tensor) – input for validation

  • Xvalid (tensor) – target for validation

  • bs (int) – batch size

  • nepoch (int) – the number of epochs

torchcs.recovery.dlmlcs.weights_init(m)

torchcs.recovery.ista_fista module

torchcs.recovery.ista_fista.fista(Y, Phi, niter=None, lambd=0.5, alpha=None, tol=1e-06, ssmode='cc')

Fast Iterative Shrinkage Thresholding Algorithm

Fast Iterative Shrinkage Thresholding Algorithm

\[{\bf Y} = {\bf \Phi}{\bf X} + \lambda \|{\bf X}\|_1 \]
Parameters

  • Y (Tensor) – Observation \({\bf Y} \in {\mathbb C}^{M\times L}\)

  • Phi (Tensor) – Observation matrix \({\bf \Phi} \in {\mathbb C}^{M\times N}\)

  • niter (int, optional) – The number of iteration (the default is None)

  • lambd (float, optional) – Regularization factor (the default is 0.5)

  • alpha (float, optional) – The update step (the default is None, which means auto computed, see upstep())

  • tol (float, optional) – The tolerance of error (the default is 1e-6)

  • ssmode (str, optional) – The type of softshrink function, 'cc' for complex-complex, 'cr' for complex-real, 'rr' for real-real.

Returns

  • X (Tensor) – Reconstructed tensor \({\bf X} \in {\mathbb C}^{N\times L}\)

  • see ista().

Examples

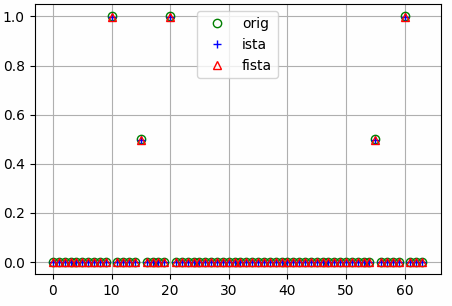
_images/ISTAFISTAdemo.png

The results shown in the above figure can be obtained by the following codes.

import torchcs as tc
import matplotlib.pyplot as plt

m, n = 32, 64
x = th.zeros(n, 1)
x[10] = x[20] = x[60] = 1
x[15] = x[55] = 0.5
Phi = th.randn(m, n)
y = Phi.mm(x)
Psi = tc.idctmtx(n)

xista = ista(y, Phi, niter=None, lambd=0.05)
xfista = fista(y, Phi, niter=None, lambd=0.05)

plt.figure()
plt.grid()
plt.plot(x, 'go', markerfacecolor='none')
plt.plot(xista, 'b+', markerfacecolor='none')
plt.plot(xfista, 'r^', markerfacecolor='none')
plt.legend(['orig', 'ista', 'fista'])
plt.show()
torchcs.recovery.ista_fista.ista(Y, Phi, niter=None, lambd=0.5, alpha=None, tol=1e-06, ssmode='cc')

Iterative Shrinkage Thresholding Algorithm

Iterative Shrinkage Thresholding Algorithm

\[{\bf Y} = {\bf \Phi}{\bf X} + \lambda \|{\bf X}\|_1 \]
Parameters

  • Y (Tensor) – Observation \({\bf Y} \in {\mathbb C}^{M\times L}\)

  • Phi (Tensor) – Observation matrix \({\bf \Phi} \in {\mathbb C}^{M\times N}\)

  • niter (int, optional) – The number of iteration. (the default is None, which means Inf)

  • lambd (float, optional) – Regularization factor (the default is 0.5)

  • alpha (float, optional) – The update step (the default is None, which means auto computed, see upstep())

  • tol (float, optional) – The tolerance of error (the default is 1e-6)

  • ssmode (str, optional) – The type of softshrink function, 'cc' for complex-complex, 'cr' for complex-real, 'rr' for real-real.

Returns

  • X (Tensor) – Reconstructed tensor \({\bf X} \in {\mathbb C}^{N\times L}\)

  • see fista().

Examples

_images/ISTAFISTAdemo.png

The results shown in the above figure can be obtained by the following codes.

import torchcs as tc
import matplotlib.pyplot as plt

m, n = 32, 64
x = th.zeros(n, 1)
x[10] = x[20] = x[60] = 1
x[15] = x[55] = 0.5
Phi = th.randn(m, n)
y = Phi.mm(x)
Psi = tc.idctmtx(n)

xista = ista(y, Phi, niter=None, lambd=0.05)
xfista = fista(y, Phi, niter=None, lambd=0.05)

plt.figure()
plt.grid()
plt.plot(x, 'go', markerfacecolor='none')
plt.plot(xista, 'b+', markerfacecolor='none')
plt.plot(xfista, 'r^', markerfacecolor='none')
plt.legend(['orig', 'ista', 'fista'])
plt.show()
torchcs.recovery.ista_fista.upstep(Phi)

computes step size

The update step size is computed by

\[\alpha = \frac{1}{{\rm max}(|\lambda|)} \]

where \(\lambda\) is the eigenvalue of \({\bf \Phi}^H{\bf \Phi}\)

Parameters

Phi (Tensor) – The observation matrix.

Returns

The computed updation step size

Return type

scalar

torchcs.recovery.matching_pursuit module

torchcs.recovery.matching_pursuit.gp()
torchcs.recovery.matching_pursuit.mp(X, D, K=None, norm=[False, True], tol=1e-06, mode=None, islog=False)

Matching Pursuit

\[x = Dz \]
\[({\bm D}_{{\mathbb I}_t}^T{\bm D}_{{\mathbb I}_t})^{-1} \]

to avoid matrix singularity

\[({\bm D}_{{\mathbb I}_t}^T{\bm D}_{{\mathbb I}_t} + C {\bm I})^{-1} \]

where, \(C > 0\).

Parameters

  • tensor (D) – signal vector or matrix, if \({\bm X}\in{\mathbb R}^{M\times L}\) is a matrix, then apply OMP on each column

  • tensor – overcomplete dictionary ( \({\bm D}\in {\mathbb R}^{M\times N}\) )

Keyword Arguments

  • K (int) – The sparse degree (default: size of \({\bm x}\))

  • norm (list of bool) – The first element specifies whether to normalize data, the second element specifies whther to normalize dictionary. If True, will be normalized by subtracting the mean and dividing by the l2-norm. (default: [False, True])

  • tol (float) – The tolerance for the optimization (default: {1.0e-6})

  • mode (str) – Complex mode or real mode, 'cc' for complex–>complex, 'cr' for complex–>real, 'rr' for real–>real

  • islog (bool) – Show more log info.

torchcs.recovery.matching_pursuit.omp(X, D, K=None, C=1e-06, norm=[False, False], tol=1e-06, method='pinv', mode=None, device='cpu', islog=False)

Orthogonal Matching Pursuit

ROMP add a small penalty factor \(C\) to

\[x = Dz \]
\[({\bm D}_{{\mathbb I}_t}^T{\bm D}_{{\mathbb I}_t})^{-1} \]

to avoid matrix singularity

\[({\bm D}_{{\mathbb I}_t}^T{\bm D}_{{\mathbb I}_t} + C {\bm I})^{-1} \]

where, \(C > 0\).

Parameters

  • tensor (D) – signal vector or matrix, if \({\bm X}\in{\mathbb R}^{M\times L}\) is a matrix, then apply OMP on each column

  • tensor – overcomplete dictionary ( \({\bm D}\in {\mathbb R}^{M\times N}\) )

Keyword Arguments

  • K (int) – The sparse degree (default: size of \({\bm x}\))

  • C (float) – The regularization factor (default: 1.0e-6)

  • norm (list of bool) – The first element specifies whether to normalize data, the second element specifies whther to normalize dictionary. If True, will be normalized by subtracting the mean and dividing by the l2-norm. (default: [False, False])

  • tol (float) – The tolerance for the optimization (default: {1.0e-6})

  • method (str) – The method for solving new sparse coefficients.

  • mode (str) – Complex mode or real mode, 'cc' for complex–>complex, 'cr' for complex–>real, 'rr' for real–>real.

  • islog (bool) – Show more log info.

Examples

_images/MPOMPdemo.png

The results shown in the above figure can be obtained by the following codes.

import torch as th
import torchcs as tc
import matplotlib.pyplot as plt

seed = 2021
f0, f1, f2, f3 = 50, 100, 200, 400
Fs = 800
Ts = 0.32
Ns = int(Ts * Fs)
R = 2
K = 7

t = th.linspace(1, Ns, Ns).reshape(Ns, 1) / Fs
pit2 = 2. * th.pi * t
x = 0.3 * th.cos(pit2 * f0) + 0.6 * th.cos(pit2 * f1) + 0.1 * th.cos(pit2 * f2) + 0.9 * th.cos(pit2 * f3)

f = th.linspace(-Fs / 2., Fs / 2., Ns).reshape(Ns, 1)
X = th.fft.fftshift(th.fft.fft(x, dim=0))

M = Ns
N = int(Ns * R)
Psi = tc.odctdict((M, N))
# Psi = tc.idctmtx(N)

z, _ = tc.mp(x, Psi, K=K, norm=[False, False], tol=1.0e-6, islog=False)
xmp = Psi.mm(z)
Xmp = th.fft.fftshift(th.fft.fft(xmp, dim=0))

z, _ = tc.omp(x, Psi, K=K, C=1e-1, norm=[False, False], tol=1.0e-6, method='pinv', islog=False)
xomp = Psi.mm(z)
Xomp = th.fft.fftshift(th.fft.fft(xomp, dim=0))

xgp = x
Xgp = X
plt.figure()
plt.subplot(221)
plt.grid()
plt.plot(t, x, '-r')
plt.subplot(222)
plt.grid()
plt.plot(f, X.abs(), '-r')
plt.subplot(223)
plt.grid()
plt.plot(x, '-*r')
plt.plot(xmp, '-sg')
plt.plot(xomp, '-+b')
plt.plot(xgp, '--k')
plt.legend(['Real', 'MP', 'OMP', 'GP'])
plt.subplot(224)
plt.grid()
plt.plot(X.abs(), '-*r')
plt.plot(Xmp.abs(), '-sg')
plt.plot(Xomp.abs(), '-+b')
plt.plot(Xgp.abs(), '--k')
plt.legend(['Real', 'MP', 'OMP', 'GP'])
plt.show()

Module contents